Fizično

električno polje

električno polje
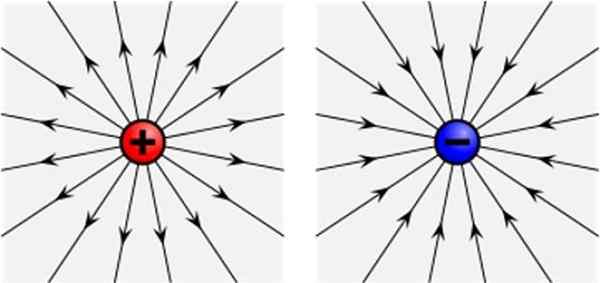
Električno polje pozitivnega (levo) in negativno (desno). Vir: Wikimedia Commons

Kaj je električno polje?

On električno polje Lastnost je, da imajo predmeti, napolnjeni z vplivom na okoliški prostor, ki ga zaznavajo drugi električno nabita telesa. Toda za razliko od električne sile med obremenitvami je električno polje odvisno le od obremenitve, ki ga proizvaja.

Michael Faraday (1791-1867), angleški fizik, je koncept polja ustvaril tako, da je opazil, da vsak električni naboj vpliva.

Niti ni treba, da so obremenitve v materialnem mediju, saj lahko interakcijo damo v vakuumu.

Za vizualizacijo oblike električnega polja predpostavimo posebno in pozitivno obremenitev, imenovano +Q, katerega velikost je tako majhna, da ni treba upoštevati njenih dimenzij. Polje, ki ga proizvaja, lahko vpliva na druge naboje, kot je še ena pozitivna obremenitev preskusne točke Qtudi.

Preskusna obremenitev je nameščena na različnih lokacijah okoli +qtudi To je odbojnost.

Risanje sile sile na obremenitev qtudi Na vsaki točki prostora, ki ga zaseda, in ga odstranimo, je nabor črt, ki se radialno pojavijo od obremenitve +Q (glejte zgornjo sliko, na levi).

Ko ponavljate izkušnjo z negativno obremenitvijo - Q, so črte tudi radialne, vendar vstopajo v - Q. V obeh primerih so linije tangentne za vektorsko električno polje obremenitve, ki ga odhajajo, kadar je pozitivno, in dohodno, če je negativno.

Formula in enote

Če je v prostoru prostora, je električno polje In, Električni naboj Qtudi Izkušnje, zahvaljujoč njemu, sile, ki jo je dal:

Vam lahko služi: Naključna napaka: formula in enačbe, izračun, primeri, vaje

F = qtudiIn

Tako da:

Električna poljska enota v mednarodnem sistemu enot je Newton/Coulomb, ki je skrajšana N/C. Običajno je izraziti tudi električno polje glede na skalarno velikost, imenovano električni potencial, v tem primeru je polje za polje volt/meter (v/m).

Električno polje natančnega bremena

Polje In nastaja nekaj predmeta z obremenitvijo Q. Zaradi česar je preizkusna obremenitev zelo majhna, to je, da je Qtudi nagiba k 0, vektorju In je:

Z Ftudi sila med Q in Qtudi.

Namen, ko prevzamete mejo.

Če je točno točno breme, po Coulombovem zakonu sila med obtožbami Q in Qtudi, Oba ločena razdalja r, poda::

V tej enačbi je K elektrostatična konstanta in enota vektor v smeri črte, ki združuje Q in Q in Qtudi je:

Zamenjava tega izraza v definiciji polja se dobi:

 Tako da polje In, Izdelana s točno obremenitvijo Q v točki P je:

Tako, In Ni odvisno od preskusne obremenitve, ampak od obremenitve, ki ga proizvaja. The velikost polja je neposredno sorazmerno z velikostjo obremenitve in obratno sorazmerno s kvadratom razdalje med obremenitvijo in točko P.

In kot je navedeno na začetku nagovor S polja je radialna in smer odhaja do obremenitve, ko je pozitivna, in dohodni, ko je negativen.

Intenzivnost električnega polja

Električno polje je vektor, njegova intenzivnost pa se nanaša na njegov modul ali velikost, ki je označena brez krepkega. Za točno obremenitev je intenzivnost njegovega električnega polja preprosto:

Vam lahko služi: površna dilatacija: formula, koeficienti in primeri

 In ker je modul zneska, je vedno pozitiven.

Na primer intenzivnost električnega polja, ki ga proizvaja obremenitev q = - 4.3 μC (μc se glasi "MicroCoulomb" in je enakovreden milijonku kuloma), na razdalji 2 cm od obremenitve, je:

Upoštevajte, da je razdalja 2 cm postala metri in se pomnoži z močjo 10−2, Ker je elektrostatična konstanta v enotah, če. In čeprav je obremenitev negativna, je intenzivnost polja, ki ga proizvaja, vedno pozitivna, vendar vektor električnega polja prihaja do obremenitve, kot je bilo že razloženo.

Primeri električnega polja

1. Električno polje diskretne porazdelitve obremenitev

Nabor posebnih stroškov se imenuje Diskretna porazdelitev obremenitve. V tem primeru se izračunava električno polje v točki P izračuna z uporabo Načelo superpozicije, ki je vsota vektorja polja, ki ga vsaka obremenitev proizvede v P:

Inmreža = In1 + In2 + In3 +..

Naslednja slika prikazuje porazdelitev, sestavljeno iz petih posebnih obremenitev in električnega polja, ki ga vsak proizvede v točki P:

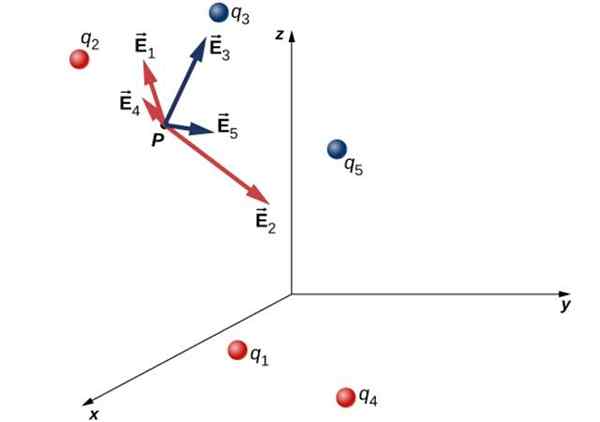Električno polje v točki P zaradi diskretne porazdelitve obremenitev
  • Obremenitve q3 in q5 So negativni in področje, ki ga proizvajajo. Odlikovani so v modri barvi.
  • Tovore q1, q2 in q4 So pozitivni, ustvarjajo vidno polje v rdeči barvi.

2. Električno polje neprekinjene porazdelitve obremenitev

Nenehna porazdelitev obremenitve je sestavljena iz razširjenega predmeta, električnega naloženega, kot je tisti, prikazan na naslednji sliki. Ker ima predmet občutne dimenzije, se polje, ki ga del telesa proizvede v P.

Vam lahko služi: Kirchhoffovi zakoni

Recimo, da se vzame majhen električni naboj omenjenega predmeta, imenovan DQ in domnevno pozitiven, kar prinaša v majhnem prispevku k skupnemu električnemu polju. Ta prispevek je razlika v vektorju električnega polja DIn.

Ker je obremenitev DQ zelo majhna, je njegovo polje podobno kot točna obremenitev, tako da je mogoče enačbo uporabiti pred ogledom:

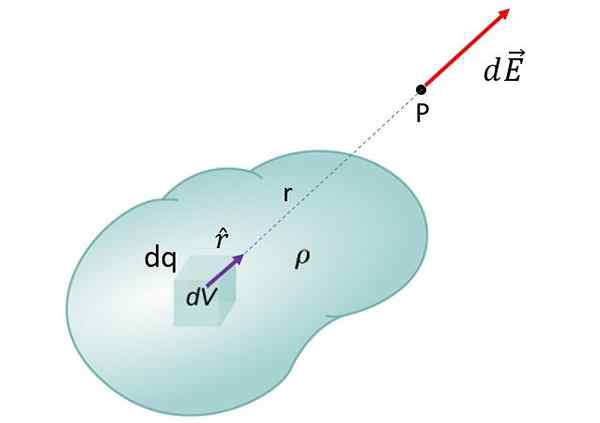Za izračun električnega polja podaljšanega predmeta je integriran predvsem. Gostota obremenitve (obremenitev na enoto prostornine) je označena kot ρ

Za pridobitev skupnega polja predmeta v točki P se dodajo prispevki vseh DQ, ki jih je mogoče vzeti na objektu. To vodi v integral:

Vaja rešena

Točna obremenitev q = 2.0 × 10−8 C je nameščen na točki P znotraj električnega polja, v katerem doživlja naraščajoča sila magnitude 4.0 × 10−6 N. Izračunati:

a) električno polje v p

b) sila na obremenitvi q = −1.0 × 10−8 C, ki se nahaja v str.

Rešitev

Biti velikost električnega polja, v katerem je obremenitev. Na podlagi tega področja ta obremenitev doživlja silo navzgor, tako da:

F = q ∙ e

Tako:

E = f /q = 4.0 × 10-6 N/ 2.0 × 10-8 C = 200 n/c.

Biti pozitiven breme, sila in polje imajo isto smer in pomen.

Rešitev b

Obseg sile, ki deluje na to, kar je:

Ko je to breme negativno, imata sila in polje isto smer, vendar nasprotna čutila.

Reference

  1. Bauer, w. 2011. Fizika za inženiring in znanosti. Zvezek 2. MC Graw Hill. 
  2. Poljski in električni potencial točnega obremenitve. Pridobljeno iz: sc.Ehu.je.
  3. Resnick, r. (1999). Fizično. Vol. 1. 3. izd. v španščini. Continental uredništvo s.Do. od c.V.
  4. Sears, z. (2016). Univerzitetna fizika s sodobno fiziko. 14. Ed. Zvezek 1. Pearson.
  5. Univerzitetna fizika. Električno polje. Vol. 2. Pridobljeno iz: OpenStax.org.