Občutljiv koncept toplote, formule in vaje razrešene

On Občutljiva toplota To je toplotna energija, ki se prinaša objektu. Je nasprotno od latentne toplote, pri kateri toplotna energija ne zvišuje temperature, ampak spodbuja fazno spremembo, na primer od trdne do tekočine.

Primer pojasnjuje koncept. Recimo, da imamo lonec s temperaturo vode 20 ° C. Ko ga postavimo v rog, priložena toplota počasi zviša temperaturo vode na 100 ° C (temperatura vrenja vode na morju). Dobavljena toplota se imenuje občutljiva toplota.

Vročina, ki segreje vaše roke, je občutljiva toplota. Vir: Pixabay

Ko voda doseže temperaturo vrenja, toplota, ki jo dobavlja Hornilla, ne poveča več temperature vode, kar ostane pri 100 ° C.  V tem primeru se dobavljena toplotna energija vlaga v izhlapevanje vode. Dobavljena toplota je latentna, ker ni zvišala temperature, ampak je povzročila spremembo tekoče faze v plinsko fazo.

Eksperimentalno dejstvo je, da je občutljiva toplota, potrebna za dosego določene temperaturne spremembe, neposredno sorazmerna s to variacijo in maso predmeta.

[TOC]

Koncept in formule

Opazili so, da je poleg mase in temperaturne razlike občutljiva toplota odvisna tudi od materiala. Zaradi tega se konstanta sorazmernosti med občutljivo toploto in produktom mase s temperaturno razliko imenuje specifična toplota.

Količina občutljive toplote je odvisna tudi od tega, kako se postopek izvaja. Na primer, drugače je, če se postopek izvaja v konstantni volumnu kot konstanten tlak.

Formula za občutljivo toploto v procesu izobarično, to pomeni stalen pritisk, kot sledi:

Q = cp . m (tF - TYo)

V prejšnji enačbi Q To je občutljiva toplota, ki se dobavi masnemu objektu m, ki je dvignila začetno temperaturo T_Yo Do končne vrednosti Tf. V prejšnji enačbi se pojavi tudi cstr, ki je specifična toplota materiala s konstantnim pritiskom, ker je bil postopek izveden na ta način.

Upoštevajte, da je občutljiva toplota pozitivna, če jo objekt absorbira in povzroči dvig temperature.

V primeru, da je na voljo plin, zaprt v togi posodi, bo postopek izokorično, torej pri konstantni glasnosti; In formula občutljive toplote bo napisana tako:

Vam lahko služi: valovito gibanje: značilnosti, vrste valov, primeri

Q = cv. m . (TF - TYo)

Adiabatski koeficient γ

Razmerje med specifično toploto pri konstantnem tlaku in specifično toploto pri konstantni prostornini za isti material ali snov se imenuje Adiabatski koeficient, ki je na splošno označen s črko Gamma Gamma γ.

On Adiabatski koeficient je večji od enote. Toplota, potrebna za dvig temperature telesa grama mase do stopnje, je v izobaričnem procesu večja kot v izokoriju.

To je zato, ker se v prvem primeru uporablja del toplote za mehansko delo.

Poleg specifične toplote je običajno opredeljena toplotna zmogljivost telesa. To je količina toplote, potrebne za dvig temperature tega telesa.

Toplotna zmogljivost c

Toplotna zmogljivost je označena z C velike črke, medtem ko specifična toplota z c nižji primer. Razmerje med obema zneskoma je:

C = c⋅ m

Kje m To je masa telesa.

Uporablja se tudi molarna specifična toplota, ki je opredeljena kot količina občutljive toplote, potrebne za dvig do Celzija ali Kelvina temperature.

Specifična toplota v trdnih snovi, tekočinah in plinih

Specifična molarna toplota večine trdnih snovi ima vrednost blizu 3 krat R, kje R Je univerzalna konstanta plinov. R = 8.314472 j/(mol ℃).

Na primer, aluminij ima specifično molarno toploto 24.2 j/(mol ℃), Baker 24,5 j/(mol ℃), zlato 25.4 J/(mol ℃), in sladko železo 25.1 J/(mol ℃). Upoštevajte, da so te vrednosti blizu 3R = 24,9 j/(mol ℃).

Po drugi strani je za večino plinov določena toplota blizu N (r/2), kje je n celo število in R Je univerzalna konstanta plinov. Celo število n je povezan s številom stopenj svobode molekule, ki tvori plin.

Na primer, v idealnem monoatomskem plinu, katerega molekula ima le tri stopnje svobode, je specifična molarna toplota do konstantne prostornine 3 (r/2). Če pa je idealen diatomični plin, sta dodatno dve rotacijski stopnji, torej cv = 5 (r/2).

Vam lahko služi: polkrog: Kako izračunati obod, območje, centroid, vaje

V idealnih plinih je izpolnjeno naslednje razmerje med specifično toplotno toploto in konstantno prostornino: cstr = cv + R.

Stranska omemba si zasluži vodo. V tekočem stanju pri 25 ℃ voda ima cstr = 4.1813 J/(g ℃), Vodna para pri 100 stopinjah ima Celsius cstr = 2,080 j/(g ℃) In vodni led do ničelne stopnje ima Celzija cstr = 2,050 j/(g ℃).

Razlika z latentno toploto

Snov najdete v treh stanjih: trdna, tekoča in plinasta. Za spremembo države je potrebna energija, vendar se vsaka snov nanjo odzove na drugačen način glede na njegove molekularne in atomske značilnosti.

Ko se trdna topi ali tekočina izhlapi, temperatura predmeta ostane konstantna, dokler vsi delci niso spremenili statusa.

Zato je možno, da je ena snov hkrati v ravnotežju v dveh fazah: trdna - tekoča ali tekoča - para, na primer. Količina snovi lahko prehaja iz enega stanja v drugo z dodajanjem ali odstranjevanjem malo toplote, medtem ko temperatura ostane pritrjena.

Toplota, dobavljena materialu, povzroči, da njeni delci hitreje vibrirajo in povečajo njegovo kinetično energijo. To pomeni dvig temperature.

Možno je, da je energija, ki jo pridobijo, tako velika, da se ne vrnejo več v svoj ravnotežni položaj in povečajo ločitev med njimi. Ko se to zgodi, se temperatura ne poveča, vendar snov prehaja iz trdne v tekočino ali plinsko tekočino.

V vročini, ki je potrebna za to, je znana kot latentna toplota. Zato je latentna toplota toplota, s katero lahko snov spremeni fazo.

Tu je razlika z občutljivo toploto. Snov, ki absorbira občutljivo toploto, poveča njegovo temperaturo in ostane v istem stanju.

Kako izračunati latentno toploto?

Latentna toplota se izračuna z enačbo:

Q = m . L

Kje L To je lahko specifična toplota uparjanja ali fuzije. Enote L So energijo/masa.

Znanstveniki so dali številne toplotne poimenovanja, odvisno od vrste reakcije, v kateri sodeluje. Tako je na primer toplota reakcije, toplota zgorevanja, toplota strjevanja, toplota raztopine, toplota sublimacije in mnogi drugi.

Vam lahko služi: kinetična energija: značilnosti, vrste, primeri, vaje

Vrednosti številnih teh vrst toplote za različne snovi so tabelirane.

Rešene vaje

Primer 1

Predpostavimo eno, ki ima 3 kg masnega aluminija. Sprva je pri 20 ° C in želite zvišati njeno temperaturo do 100 ° C. Izračunajte potrebno občutljivo toploto.

Rešitev

Najprej moramo vedeti specifično toploto aluminija

cstr = 0,897 j / (g ° C)

Torej bo količina toplote, potrebne za ogrevanje kosa aluminija

Q = cstr m (tf - ti) = 0,897 * 3000 * (100 - 20) J

Q = 215280 J

Primer 2

Izračunajte količino toplote, potrebne za ogrevanje 1 liter vode od 25 ° C do 100 ° C na morju. Rezultat izraža tudi v kilokalorih.

Rešitev

Prva stvar, ki bi si jo morali zapomniti, je, da 1 liter vode tehta 1 kg, to je 1000 gramov.

Q = cstr m (tf - ti) = 4,1813 j/(g ℃) * 1000 g * (100 ℃ - 25 ℃) = 313597,5 J

Kalorija je enota energije, ki je opredeljena kot občutljiva toplota, potrebna za dvig grama vode na Celzija. Zato je 1 kalorija enakovredna 4.1813 Joules.

Q = 313597,5 J * (1 Cal / 4,1813 J) = 75000 apno = 75 kcal.

Primer 3

Košček materiala 360,16 gramov se segreje od 37 ℃ do 140 ℃. Dobavljena toplotna energija je 1150 kalorij.

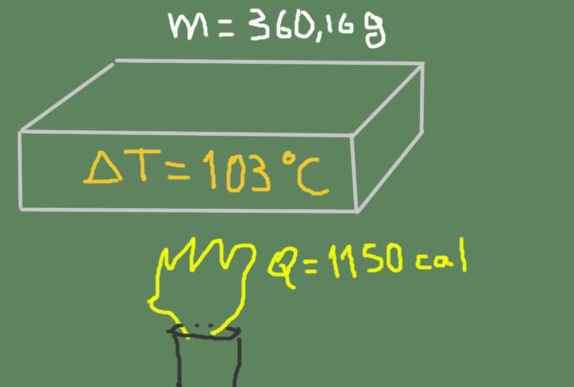Segrevanje vzorca. Vir: Self Made.

Poiščite specifično toploto materiala.

Rešitev

V skladu s formulo lahko napišemo specifično toploto na podlagi občutljive toplote, mase in temperaturne spremembe:

cstr = Q /(m ΔT)  

Zamenjava podatkov imamo naslednje:

cstr = 1150 cal / (360,16 g * (140 ℃ - 37 ℃)) = 0.0310 cal / (g ℃)

Ker pa je kalorija enakovredna 4.1813 J, se rezultat lahko izrazi tudi kot

cstr = 0,130 j / (g ℃)

Reference

1. Giancoli, d.  2006. Fizika: načela z aplikacijami. 6^th. Ed. Dvorana Prentice. 400 - 410.
2. Kirkpatrick, l. 2007. Fizika: pogled na svet. 6^ta Skrajšana izdaja. Cengage učenje. 156 - 164.
3. Tippens, str. 2011. Fizika: pojmi in aplikacije. 7. Revidirana izdaja. McGraw Hill. 350 - 368.
4. Rex, a. 2011. Osnove fizike. Pearson. 309 - 332.
5. Sears, Zemansky. 2016. Univerzitetna fizika s sodobno fiziko. 14^th. Zvezek1. 556 - 553.
6. Serway, r., Vulle, c. 2011. Osnove fizike. 9^na Cengage učenje. 362 - 374.