Zgodovina matematične biologije, objekt študija, aplikacij

The Matematična biologija ali Biomatematika je veja znanosti, ki je odgovorna za razvoj numeričnih modelov, ki uspejo simulirati različne naravne pojave, povezane z živimi bitji; torej pomeni uporabo matematičnih orodij za preučevanje naravnih ali bioloških sistemov.

Kot je mogoče razumeti v svojem imenu, je biomattematika interdisciplinarno področje, ki je na presečišču znanja med biologijo in matematiko. Preprost primer te discipline bi lahko vključeval razvoj statističnih metod za reševanje problemov na področju genetike ali epidemiologije, če jih naštejemo.

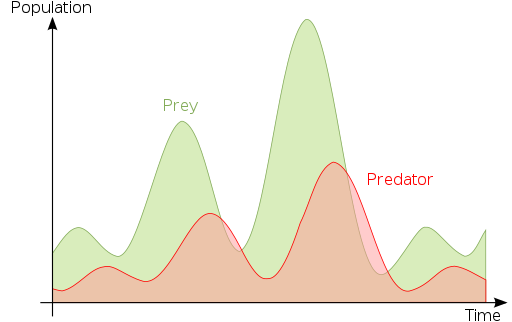Lotka-Volterra zakon za razmerje med plenilci in jezovi (vir: Curtis Newton ↯ 10:55, 20. Apr. 2010 (CEST).Prvotni nalagalec je bil Lämpel pri nemški Wikipediji. [CC BY-SA 3.0 (http: // creativeCommons.Org/licence/by-sa/3.0/)] prek Wikimedia Commons)

Na tem področju znanja je normalno, da matematični rezultati izhajajo iz bioloških problemov ali se uporabljajo za njihovo reševanje, vendar so nekaterim raziskovalcem uspeli rešiti matematične težave, ki temeljijo na opazovanju bioloških pojavov, zato ni enosmerni odnos med Oba področja znanosti.

Iz zgoraj navedenega je mogoče zagotoviti, da je matematični problem konec, za katerega se uporabljajo biološka orodja in obratno; da je biološki problem konec, za katerega se uporabljajo zelo raznolika matematična orodja.

Trenutno področje matematične biologije raste s pospešenimi koraki in velja za eno najsodobnejših in najbolj vznemirljivih aplikacij matematike. Zelo je uporaben ne samo v biologiji, ampak v biomedicinskih znanostih in na področju biotehnologije.

[TOC]

Zgodovina biomatematike

Matematika in biologija sta dve znanosti z množico aplikacij. Matematika je morda stara toliko kot zahodna kultura, njen izvor sega že več let, preden je od takrat dokazana Kristus in njena uporabnost za veliko število aplikacij.

Vam lahko služi: test oksidaze: temelj, postopek in uporabe

Biologija kot znanost pa je veliko novejša, saj se njena konceptualizacija ni zgodila šele v začetku 19. stoletja, zahvaljujoč posredovanju Lamarcka, za 1800 -ih.

Odnos matematičnega in biološkega znanja je ozek od zgodnjih stopenj civilizacij, saj se je naselitev nomadskih ljudstev zgodila zahvaljujoč odkritju, da bi bilo mogoče sistematično izkoristiti naravo, ki mora imeti obvezno prvo predstavo matematiko in biološko.

V svojih načelih so biološke znanosti veljale za "obrti", saj so se nanašale predvsem na priljubljene dejavnosti, kot sta kmetijstvo ali živino; Medtem so matematiki odkrili abstrakcijo in imeli nekaj nekoliko oddaljenih aplikacij.

Sotočje med biologijo in matematiko sega v petnajsto in šestnajsto stoletje, s pojavom fiziologije, ki je znanost, ki združuje znanje, jih razvršča, jih naroči in sistematizira, ko jih uporablja matematična orodja, kadar je.

Thomas Malthus

To je Thomas Malthus, sodobni ekonomist z Lamarckom, ki je postavil precedens za začetek matematične biologije, saj je prvi postavil matematični model, ki je razložil dinamiko prebivalstva, ki temelji na naravnih virih.

Malthusovi pristopi so bili pozneje bolj razviti in izdelani, danes pa so del osnove ekoloških modelov, ki se uporabljajo za razlago odnosa med plenilci in njihovim plenom, na primer.

Predmet preučevanja matematične biologije

Matematična biologija je interdisciplinarno znanstveno področje. Vir: Konstantin Kolosov - Pixabay

Matematična biologija je znanost, ki je posledica integracije različnih matematičnih orodij z biološkimi, eksperimentalnimi ali ne, ki si prizadeva izkoristiti "moč" matematičnih metod, da bi bolje razlagali svet živih bitij, njihovih celic in njegovih molekul.

Lahko vam služi: prehranska veriga: elementi, trofična piramida in primeri

Ne glede na stopnjo vključene tehnološke zapletenosti je matematična biologija sestavljena iz "preprostega" pomisleka, da obstaja analogija med dvema procesoma, in sicer:

- Kompleksna struktura živega bitja je rezultat uporabe preprostega "kopiranega" in "rezanja in spajanja" ali "Splicing"(Na primer) za začetne informacije, ki so v zaporedju DNK (deoksiribonukleinska kislina).

- Rezultat F (Ω) uporabe računalniške funkcije do ureditve W lahko dobimo z uporabo kombinacije preprostih osnovnih funkcij za W.

Področje matematične biologije uporablja področja matematike, kot so izračun, teorije verjetnosti, statistika, linearna algebra, algebrska geometrija, topologija, diferencialne enačbe, dinamične sisteme, kombinatorična in teorija kodiranja.

V zadnjem času je bila ta disciplina zelo izkoriščena za kvantitativno analizo različnih vrst podatkov, saj so se biološke znanosti posvetile velikim masam podatkov.

Pravzaprav mnogi raziskovalci menijo, da je velika eksplozija bioloških podatkov "ustvarila" potrebo po razvoju novih in bolj zapletenih matematičnih modelov za analizo, pa tudi računskih algoritmov in bistveno bolj zapletenih statističnih metod.

Prijave

Ena najpomembnejših aplikacij matematične biologije je povezana z analizo sekvenc DNK, vendar je ta znanost vključena tudi v modeliranje epidemij in pri preučevanju širjenja živčnih signalov.

Uporablja se za preučevanje nevroloških procesov, kot so Parkinsonova bolezen, Alzheimerjeva in amiotrofična lateralna skleroza.

Lahko vam služi: Erihrous: Značilnosti, struktura, funkcije

Zelo koristno je za preučevanje evolucijskih procesov (teoretičnosti) in za razvoj modelov, ki pojasnjujejo odnos živih bitij med seboj in njihovim okoljem, torej za ekološke pristope.

Modeliranje in simulacija različnih vrst raka je tudi dober primer več aplikacij, ki jih ima danes matematična biologija, zlasti glede simulacije interakcij med celičnimi populacijami.

Primer analize sekvenc DNK, ki se običajno uporabljajo v genomiki (vir: RADTK172 [CC BY-SA 4.0 (https: // creativeCommons.Org/licence/by-sa/4.0)] prek Wikimedia Commons)

Biomatematika je zelo napredna tudi na področju računske nevroznanosti, v študijah populacije in filogenomske in genomske dinamike na splošno.

V tej zadnji veji genetike je bila zelo pomembna, saj je eno najvišjih rastnih področij v zadnjih letih, saj je stopnja pridobivanja podatkov izjemno visoka, kar zasluži nove in boljše tehnike za njegovo obdelavo in analizo.

Reference

1. Andersson, s., Larsson, k., Larsson, m., & Jacob, m. (Eds.). (1999). Biomatematika: matematika bioslacij in biodinamike. Elsevier.
2. Elango, str. (2015). Vloga matematike v biologiji.
3. Friedman, a. (2010). Kaj je matematična biologija in kako koristna je. Obvestila AMS, 57 (7), 851-857.
4. Hofmeyr, j. H. S. (2017). Matematika in biologija. Južnoafriški časopis za znanost, 113 (3-4), 1-3.
5. Kari, l. (1997). Računalništvo DNK: Prihod biološke matematike. Matematični Intelligencer, 19 (2), 9-22.
6. Pacheco castelao, j. M. (2000). Kaj je matematična biologija?
7. Reed, m. C. (2004). Zakaj je matematična biologija tako težka? Obvestila AMS, 51 (3), 338-342.
8. Ulam, s. M. (1972). Pod ideje in možnosti v biomatematiki. Letni pregled biofizike in bioinženiringa, 1 (1), 277-292.