Ravnotežje snov, kaj je, splošna enačba, tipi

On materialno ravnovesje To je število komponent, ki pripadajo sistemu ali v študijskem postopku. To ravnovesje je mogoče uporabiti skoraj za katero koli vrsto sistema, saj se domneva, da mora vsota mase takšnih elementov ostati konstantna pri različnih meritvah.

S komponento lahko razumete do marmorjev, bakterij, živali, lesa, sestavine za torto; in v primeru kemije, molekul ali ionov ali natančneje, spojin ali snovi. Nato mora skupna masa molekul, ki vstopajo v sistem, z ali brez kemične reakcije, ostati konstantna; Dokler ni izgub puščanja.

V praksi je predstavljenih neštetih težav, ki lahko vplivajo na ravnovesje snovi, poleg tega, da upoštevajo različne pojave snovi in ​​učinek številnih spremenljivk (temperatura, tlak, pretok, vznemirjenje, velikost reaktorja itd.).

Na papirju pa se morajo izračuni ravnotežja snovi sovpadati; to pomeni, da masa kemičnih spojin ne sme kadar koli izginiti. Ustvarjanje tega ravnovesja je analogno, da v ravnovesje postavite kup kamnin. Če se ena od množic uide, vse razpade; V tem primeru bi to pomenilo, da so izračuni napačni.

Splošna enačba stanja predmeta

V vsakem sistemu ali postopku je treba najprej določiti, kakšne so njihove meje. Od njih bo znano, katere spojine vstopijo ali zapustijo. To je priročno, še posebej, če je treba upoštevati več procesnih enot. Ko upoštevajo vse enote ali podsistemi, se govori o bilanci stanja splošne snovi.

Ta ravnovesje ima enačbo, ki jo je mogoče uporabiti za kateri koli sistem, ki upošteva zakon o ohranjanju množice. Enačba je naslednja:

Vam lahko služi: svinčeno klorid: lastnosti, struktura, uporabe

E + g - s - c = a

Kjer je E količina snovi vstopi Sistemu; G je tisto, kar vem generiranje Če se v procesu pojavi kemična reakcija (kot v reaktorju); S je kaj pride ven sistema; C je tisto, kar vem porabiti, Spet, če obstaja reakcija; In končno, to je tisto, kar vem akumulira.

Poenostavitev

Če v sistemu ali postopku, ki ga preučujemo, ni kemične reakcije, sta G in C vredna nič. Tako enačba ostaja:

E - S = a

Če se sistem upošteva tudi v stacionarnem stanju, brez pomembnih sprememb spremenljivk ali pretokov komponent, se v notranjosti ne kopiči nič. Zato je vredno nič, enačba pa še bolj poenostavi:

E = s

To pomeni, da je količina snovi, ki vstopi, enaka tisti, ki izide. Nič se ne more izgubiti ali izginiti.

Po drugi strani pa, če obstaja kemična reakcija, vendar bo sistem v stacionarnem stanju, bosta G in C imela vrednosti in bosta še naprej enaka:

E + G - S - C = 0

E + G = S + C

Kar pomeni, da je v reaktorju masa reagentov, ki vstopajo, in izdelkov, ki jih ustvarjajo v njem.

Primer njegove uporabe: ribe v reki

Predpostavimo, da se preučuje število rib v reki, katere bregove predstavljajo mejo sistema. Znano je, da v povprečju vstopi 568 rib na leto, 424 se roje (generira), 353 umre (poraba) in 236 se izseli ali zapusti.

Uporaba splošne enačbe, potem pa imate:

568 + 424 - 353 - 236 = 403

To pomeni, da se s 403 ribami nabirajo v reki; to pomeni, da na leto reka obogati več rib. Če bi imel negativno vrednost, bi to pomenilo, da se število rib zmanjšuje, morda na negativne vplive na okolje.

Lahko vam služi: ionske sile: enote, kako jo izračunati, primeri

Fantje

Iz splošne enačbe si lahko mislite, da obstajajo štiri enačbe za različne vrste kemičnih procesov. Vendar je ravnovesje zadeve razdeljeno na dve vrsti glede na drugo merilo: čas.

Diferencialno ravnovesje

V ravnovesju diferencialne snovi je količina komponent znotraj sistema v določenem času ali času. Te množične količine so izražene z enotami časa in zato predstavljajo hitrost; Na primer kg/h, kar kaže na to, koliko kilometrov vstopi, zapusti, kopiči, ustvarja ali porabi v eni uri.

Tako da obstajajo masi (ali volumetrični tokovi, z gostoto), mora biti sistem na splošno odprt.

Integralno ravnovesje

Ko je sistem zaprt, tako kot pri reakcijah, ki se izvajajo v vmesnih reaktorjih (vrsta serije), se množice njegovih komponent običajno zanimajo pred in po postopku; torej med začetnimi in zadnjimi T -krat.

Zato se količine izražajo kot zgolj mase in ne hitrosti. Ta vrsta ravnotežja je narejena duševno, ko se uporablja mešalnik: masa sestavin, ki vstopajo, mora biti enaka tisti, ki je ostala po motorju.

Primer vaja

Zaželeno je razredčiti pretok 25 -odstotne raztopine metanola v vodi, pri čemer je ena od 10% koncentracije, bolj razredčena, tako, da nastane 100 kg/h iz 17 -odstotne raztopine metanola. Koliko obeh raztopin metanola mora pri 25 in 10%vstopiti v sistem na uro, da to doseže? Predpostavimo, da je sistem v nepremičnem stanju

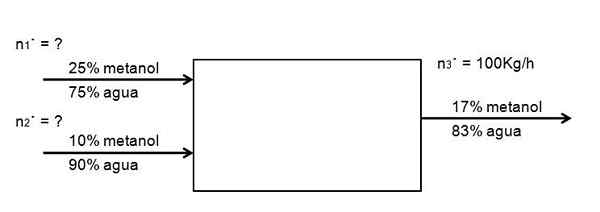
Vam lahko služi: saponifikacija

Naslednji diagram prikazuje izjavo:

Diagram pretoka za redčenje raztopine metanola. Vir: Gabriel Bolívar.

Ni kemijske reakcije, zato mora biti količina metanola enaka tisti, ki izide:

In_Metanol = S_Metanol

0,25 n₁^· + 0,10 n₂^· = 0,17 n₃^·

Znana je le vrednost n₃^·. Ostali so neznani. Za rešitev te enačbe dveh neznank je potrebno drugo ravnovesje: voda. Potem je enako ravnovesje za vodo:

0,75 n₁^· + 0,90 n₂^· = 0,83 n₃^·

Vrednost N se očisti za vodo₁^· (Lahko je tudi n₂^·)::

n₁^· = (83 kg/h - 0,90n₂^·)/ (0,75)

Zamenjava nato n₁^· V enačbi ravnotežja za metanol in reševanje za n₂^· Imaš:

0,25 [(83 kg/h - 0,90n₂^·)/ (0,75)] + 0,10 n₂^· = 0,17 (100 kg/h)

n₂^· = 53,33 kg/h

In pridobiti n₁^· Samo odštejte:

n₁^· = (100-53,33) kg/h

= 46,67 kg/h

Zato morate na uro vstopiti v sistem 46,67 kg 25%raztopine metanola in 53,33 kg 10%raztopine.

Reference

1. Felder in Rousseau. (2000). Osnovna načela kemičnih procesov. (Druga izdaja.). Addison Wesley.
2. Fernández Germán. (20. oktober 2012). Opredelitev ravnotežja snovi. Okrevano od: industrija.mreža