Lok (geometrija) meri, vrste lokov, primeri

On priklon, V geometriji je vsaka ukrivljena črta, ki povezuje dve točki. Ukrivljena črta, za razliko od ravne črte, je ta, katere smer je drugačna na vsaki točki istega. Nasprotno od loka je segment, saj je to naravnost, ki se pridruži dvema točkama.

Lok, ki se najpogosteje uporablja pri geometriji, je obod. Drugi loki skupne uporabe so parabolični lok, eliptični lok in katarniški lok. Oblika loka se pogosto uporablja tudi v arhitekturi kot okrasni in konstrukcijski element. To je primer pripadnikov vrat in oken, pa tudi mostov in akvaduktov.

Slika 1. Mavrica je ukrivljena črta, ki se pridruži dve točki na obzorju. Vir: Pixabay

[TOC]

Lok in njegov ukrep

Ukrep loka je njegova dolžina, ki je odvisna od vrste krivulje, ki povezuje obe točki in lokacijo le -teh.

Dolžina krožnega loka je ena najlažjih za izračun, ker je znana celotna dolžina loka ali obod kroga.

Obod kroga je dva pi krat vaš radio: P = 2 π r. Če to veste, če želite izračunati dolžino s krožnega loka kota α (Merjeno v radianih) in radiu R, Uporablja se delež:

(s / p) = (α / 2 π)

Nato čiščenje s prejšnjega izraza in nadomeščanja oboda str z izrazom, odvisno od radia R, Imaš:

S = (α / 2 π) p = (α / 2 π) (2 π r) = α r.

To pomeni, da je merilo krožnega loka produkt njene kotne odprtine s krožnim polmerom.

Za lok na splošno je težava bolj zapletena, do te mere, da so veliki misleci antike trdili, da je to nemogoča naloga.

Lahko vam služi: kaj so algebrski izrazi in ki so najpogostejši?

Šele ko se pojav diferencialnega in integralnega izračuna leta 1665, je bil problem mere katerega koli loka zadovoljivo rešiti. 

Pred izumom diferencialnega izračuna je bilo mogoče najti samo rešitve z uporabo poligonalnih linij ali obodov, ki so se približali pravemu loku, vendar te rešitve niso bile natančne. 

Vrste lokov

Z vidika geometrije so loki razvrščeni po ukrivljeni črti, ki se pridruži dvema točkama ravnine. Obstajajo druge klasifikacije glede na njegovo arhitekturno uporabo in obliko.

Krožni lok

Ko je črta, ki povezuje dve točki ravnine, kos obsega določenega polmera, obstaja krožni lok. Slika 2 prikazuje krožni lok polmera r, ki povezuje točke A in B.

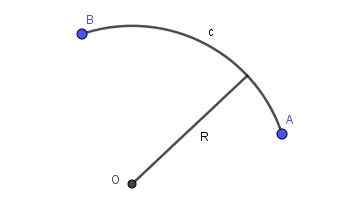Slika 2. Radio r krožni lok, ki povezuje točko A in B. Pripravil Ricardo Pérez.

Parabolični lok

Prispodoba je usmeritev, ki sledi predmetu, ki je bil vržen v zrak v poševni obliki. Ko je krivulja, ki se pridruži dve točki, prispodoba, potem obstaja parabolični lok, kot je prikazan na sliki 3.

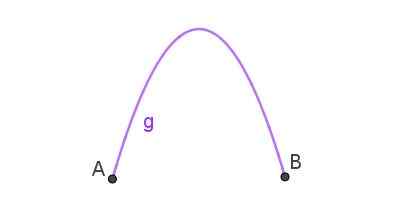Slika 3. Parabolični lok, ki povezuje točke A in B. Pripravil Ricardo Pérez.

To je oblika, ki sprejme vodni curek, ki izhaja iz cevi, ki kaže. Parabolični lok lahko opazimo v vodnih virih.

Slika 4. Parabolični lok, ki ga tvori voda iz vira v Dresdnu. Vir: Pixabay.

Katenski lok

Katenski lok je še en naravni lok. Katenarska krivulja je naravno oblikovana, ko veriga ali vrv udobno visi z dveh ločenih točk.

Vam lahko služi: kakšni so elementi kota?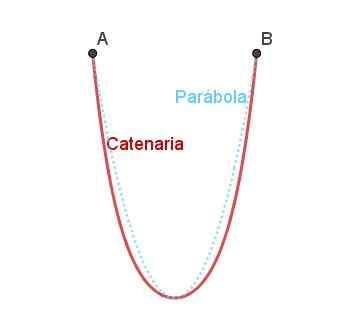 Slika 5. Katenski lok in primerjava s paraboličnim lokom. Pripravil Ricardo Pérez.

Katenarstvo je podobno paraboli, vendar ni popolnoma enako, kot je mogoče ugotoviti na sliki 4.

Obrnjen lok v obliki katanarnika se uporablja v arhitekturi kot strukturni element visoke odpornosti. Pravzaprav je mogoče dokazati, da je med vsemi možnimi oblikami najbolj odporen tip loka. 

Za izgradnjo trdnega katinarnega loka je kopirana samo oblika vrvi ali verige, nato pa se kopirana oblika obrne, da jo razmnožuje v vratih ali oknu.

Eliptični lok

Lok je eliptičen, če je krivulja, ki povezuje dve točki, razteg ali raztezanje elipse. Elipsa je opredeljena kot geometrijski kraj točk, katerih razdalja do dveh točk dane vedno doda konstantno količino.

Elipse je krivulja, ki se pojavlja v naravi: to je krivulja planeta poti okoli sonca, kot je dokazal Johannes Kepler leta 1609.

V praksi lahko narišete elipso tako. Potem je vrv napeta z označevalcem ali svinčnikom in krivulja je narisana. Košček elipse je eliptični lok. Naslednja animacija ponazarja, kako je narisana elipsa:

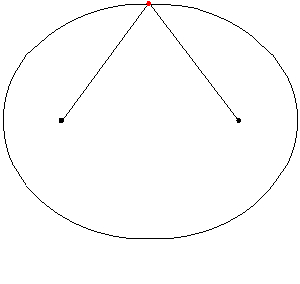Slika 5. Posen elipse z napeto vrvjo. Vir: Wikimedia Commons

Slika 6 prikazuje eliptični lok, ki povezuje točke g in h.

Slika 6. Eliptični lok, ki povezuje dve točki. Pripravil Ricardo Pérez.

Primeri lokov

Naslednji primeri se nanašajo na to, kako izračunati obod nekaterih specifičnih lokov.

Vam lahko služi: transcendentne številke: kaj so, formule, primeri, vaje

Primer 1

Slika 7 prikazuje okno, končano v krožnem loku. Dimenzije, prikazane na sliki, so na nogah. Izračunajte dolžino loka.

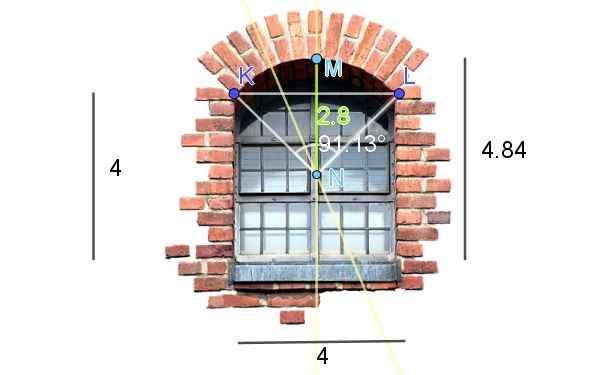Slika 7. Izračun krožne dolžine loka okna. (Lastne pripombe - okenska slika v Pixabayu)

Za pridobitev središča in polmera krožnega loka okna okna so na sliki narejene naslednje konstrukcije:

-Segment KL je narisan in narisan je njegov mediatrix.

-Potem se nahaja najvišja točka lintela, ki jo imenujemo m. Segment KM je nato upoštevan in njen mediatrix je narisan.

Prestrezanje obeh mediatric je točka N in je tudi središče krožnega loka.

-Zdaj morate izmeriti dolžino segmenta NM, ki sovpada s polmerom r krožnega loka: r = 2.8 čevljev.

-Če želite poznati dolžino loka poleg polmera, kot, ki tvori lok. Ki jih lahko določimo z dvema metodama ali se meri s transporterjem ali izmenično izračunano s pomočjo trigonometrije.

V primeru prikazanega kot, ki tvori lok, je 91.13 °, ki jih je treba pretvoriti v radiane:

 91,13 ° = 91,13 ° * π / 180º = 1,59 radianov

Končno izračunamo dolžino s loka skozi formulo S = α r.

S = 1,59 * 2.8 čevljev = 4,45 čevljev

Primer 2

Poiščite dolžino eliptičnega loka, prikazanega na sliki 8, znano r in manjša poloka s elipse.

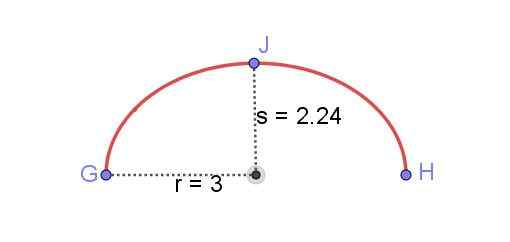Slika 8. Eliptični lok med GH. Pripravil Ricardo Pérez.

Iskanje dolžine elipse je bilo dolgo časa eden najtežjih težav matematike. Rešitve, izražene z eliptičnimi integrali, je mogoče pridobiti, vendar za numerično vrednost je treba te integrale v seriji moči razširiti. Natančen rezultat bi zahtevali neskončne izraze teh serij.

Na srečo je matematični genij hindujskega porekla Ramanujana, ki je živel med letoma 1887 in 1920, našel formulo, ki zelo natančno približa obod elipse:

Obod elipse = π [3 (r + s) - √ ((3r + s) (r + 3s))]]

Obod elipse z r = 3 cm in s = 2.24 cm je 16,55 cm. Vendar ima prikazan eliptični lok polovico te vrednosti:

Eliptična dolžina loka GH = 8.28 cm.

Reference

1. Clemens s. 2008. Geometrija in trigonometrija. Pearson Education.
2. Garcia f. Numerični postopki na Javi. Dolžina elipse. Pridobljeno iz: sc.Ehu.je
3. Dinamična geometrija. Loki. Okrevano od geometriadinamike.je
4. Pizes. Elipse in prispodobe okoli nas. Pridobljeno iz: pizessas.com
5. Wikipedija. Lok (geometrija). Okrevano od: je.Wikipedija.com