Koncepti, metode, primeri mrežaste analize

On Analiza mreže Gre za tehniko, ki se uporablja za reševanje ravnih električnih vezij. Ta postopek se lahko pojavi tudi v literaturi z imeni metode tokovi vezja o metoda Mrežaste tokove (ali zanka).

Temelj tega in drugih metod analize električnega vezja je v zakonih Kirchhoffa in Ohma. Kirchhoffovi zakoni so izražani dve zelo pomembni načeli ohranjanja v fiziki za izolirane sisteme: ohranjeni so tako električni naboj kot energija.

Slika 1. Vezja so del neštetih naprav. Vir: Pixabay.

Po eni strani je električni naboj povezan s tokom, ki premika obremenitev, v vezju pa je energija povezana z napetostjo, ki je povzročitelj, ki je odgovoren za potrebno delo, da se obremenitev ohranja v gibanju.

Ti zakoni, ki se uporabljajo za ravno vezje, ustvarijo nabor hkratnih enačb, ki jih je treba rešiti, da dobimo vrednosti toka ali napetosti.

Sistem enačb je mogoče rešiti z že znanimi analitičnimi tehnikami, kot so Pravilo Cramer, ki zahteva izračun dejavnikov za pridobitev sistemske rešitve.

Glede na število enačb se razrešijo z znanstvenim kalkulatorjem ali matematično programsko opremo. V omrežju je na voljo tudi veliko možnosti.

[TOC]

Pomembni izrazi

Preden razložimo, kako deluje, bomo začeli z opredelitvijo teh izrazov:

Podružnica: Razdelek, ki vsebuje element vezja.

Vozlišče: točka, ki povezuje dve ali več vej.

Trak: Je vsak zaprti del vezja, ki se začne in konča v istem vozlišču.

Mreža: zanka, ki ne vsebuje nobene druge vezi v notranjosti (bistvena mreža).

Metode

Analiza mreže je splošna metoda, ki služi za reševanje vezij, katerih elementi so zaporedno povezani, vzporedno ali mešani. Vezje mora biti ravno ali pa ga mora biti vsaj mogoče odplačati kot takega.

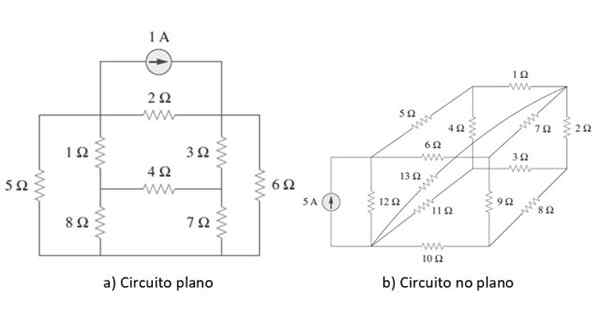Slika 2. Ravna in neflatna vezja. Vir: Aleksander, c. 2006. Temelji električnega vezja. 3. mesto. Izdaja. MC Graw Hill.

Primer vsake vrste vezja je prikazan na zgornji sliki. Ko bo točka razjasnjena, za začetek, bomo v naslednjem razdelku uporabili metodo za preprost vezje kot primer, vendar preden na kratko pregledamo zakone Ohma in Kirchhoffa.

OHM -ov zakon: Sean V Napetost, R odpor e Yo Tok ohmičnega uporovnega elementa, v katerem sta napetost in tok neposredno sorazmerna, upornost je konstanta sorazmernosti:

Vam lahko služi: Gravitacija API: lestvica in klasifikacija surove nafte

V = i.R

Zakon o napetosti Kirchhoff (LKV): V kateri koli zaprti poti, ki je potovala v eno smer, je algebrska vsota napetosti nič. To vključuje napetosti zaradi virov, uporov, induktorjev ali kondenzatorjev: ∑ e = ∑ r_Yo. Yo

Kirchhoff iz toka (LKC): V katerem koli vozlišču je algebrska vsota tokov nič enaka, ob upoštevanju, da so tokovi, ki so vpisani. Na ta način: ∑ i = 0.

Z metodo mrežastih tokov ni potrebno.

- Koraki za uporabo mrežnih analiz

Začeli bomo razlagati metodo za 2 mrežaste vezje. Postopek lahko pozneje podaljšate za večja vezja.

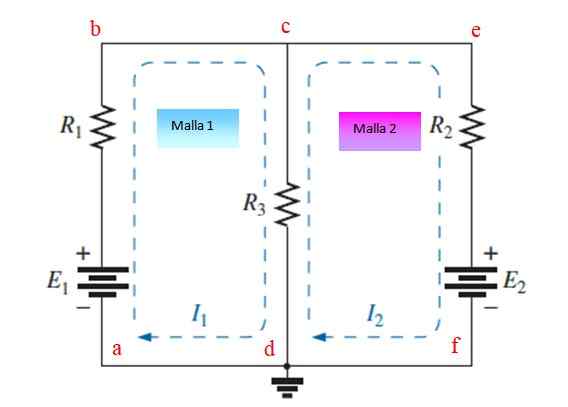Slika 3. Vezje z upori in viri, razporejenimi v dveh očesih. Vir: f. Zapata.

Korak 1

Vsaki mreži dodelite in narišite neodvisne tokove, v tem primeru so Yo₁ in Yo₂. Narisati jih je mogoče v urniku ali tudi proti donosnici.

2. korak

Za vsako mrežo uporabite zakon o napetosti Kirchhoff (LTK) in OHM. Potencialni padci so dodeljeni znak (-), medtem ko so povišanja dodeljena znak (+).

ABCDA MESH

Začenši od točke A in po pomenu toka najdemo porast potenciala v bateriji E1 (+), nato pade v R₁ (-) in nato še en padec v r₃ (-).

Hkrati odpor R₃ Prekriža ga tudi tok I₂, Toda v nasprotni smeri torej predstavlja vzpon (+). Prva enačba je taka:

In₁-R₁.Yo₁ -R₃.Yo₁ + R₃.Yo₂ = 0

Takoj upoštevanje in ponovni promotiranje izrazov:

- (R₁+R₃) Yo₁ +R₃Yo₂ = -E₁  (Enačba 1)

CEFDC mreža 

Začenši od točke in in po pomenu toka je potencialni padec R₂ (-), še en padec In₂, Ker tok vstopi skozi baterijski pol + in končno še en padec R₃ (-), hkrati tok Yo₁ Prečka R₃ V nasprotni smeri (+).

Druga enačba z navedenimi znaki ostaja na ta način:

- R₂ Yo₂ - In₂ -R₃ Yo₂ +R₃ Yo₁= 0

R₃Yo₁ - (R₂ +R₃₎ Yo₂ = E₂  (Enačba 2)

Upoštevajte, da obstajata dve enačbi z dvema neznankama in₁ in jaz₂.

Korak 3

Nato se tako oblikuje sistem enačb.

Rešene vaje

Za začetek je pomembno upoštevati naslednje:

-Povezave ali mrežaste tokove lahko dodelite poljubno smer.

-Vsako bistveno mrežo - ali "okno" -, da mora biti vezje dodeljeno tok.

Vam lahko služi: izokorični postopek

-Mesh tokovi se pokličejo z velikimi črkami, da jih ločijo od tokov, ki krožijo v vejah, čeprav v nekaterih primerih tok, ki kroži skozi vejo, lahko enak kot pri mrežici.

- Primer 1

Poiščite tokove, ki krožijo skozi vsak upor v vezju na sliki 3, če imajo elementi naslednje vrednosti:

R₁ = 20 Ω; R₂ = 30 Ω; R₃ = 10 Ω; In₁ = 12 V; In₂ = 18 V

Rešitev

Na prvem mestu je treba dodeliti tokove mreže in₁ in jaz₂ in vzemite sistem enačb, kot je bilo sklenjeno v prejšnjem razdelku, nato pa zamenjajte vrednosti, navedene v izjavi:

- (R₁+R₃) Yo₁ +R₃Yo₂ = -E₁  (Enačba 1)

R₃Yo₁ - (R₂ +R₃₎ Yo₂ = E₂     (Enačba 2)

-

-(20+30) Yo₁ + 10i₂ = -12

10i₁ - (30 +10) i₂ = 18      

--

-petdesetYo₁ + 10i₂ = -12

10i₁ - 40 i₂ = 18      

Ker gre za sistem enačb 2 x 2, ga je mogoče enostavno rešiti z redukcijo in pomnožiti s 5 drugo enačbo, da odpravimo neznano Yo₁:

-petdesetYo₁ + 10 i₂ = -12

50i₁ - 200 i₂ = 90

-     

-190 i₂= 78

Yo₂ = - 78/180 a = - 0.41 a

Tok je takoj očiščen Yo₁ katere koli od prvotnih enačb:

Yo₁ = (18 + 40 I₂) / 10 = (18 + 40 x (-0.41)) / 10 = 0.16 a

Negativni znak v toku Yo₂ pomeni, da tok v 2 mreži kroži v nasprotju z risbo.

Tokovi v vsakem uporu so naslednji:

Za odpor R₁ Tok kroži Yo₁ = 0.16 a V smislu, ki ga je narisal, z odpornostjo R₂ Tok kroži Yo₂ = 0.41 a v nasprotju z narisanim in za odpornost R₃ kroži Yo₃ = 0.16- (-0.41) a = 0.57 a dol.

Sistemska rešitev po Cramerjevi metodi

Na matrični način je sistem mogoče rešiti na naslednji način:

1. korak: Izračunajte δ

 Pomembno: Ko Δ = 0, sistem nima rešitve, je nezdružljiv sistem.

2. korak: Izračunajte δ₁

Prvi stolpec nadomestimo z neodvisnimi izrazi sistema enačb, pri čemer ohranja vrstni red, v katerem je bil sistem prvotno dvignjen:

3. korak: Izračunajte i₁

Yo₁ = Δ₁/Δ = 300/1900 = 0.16 a

4. korak: Izračunajte δ₂

 5. korak: Izračunajte i₂

Yo₂ = Δ₂/Δ = -780/1900 = -0.41 a

- Primer 2

Določite tok in napetosti skozi vsak upor v naslednjem vezju s pomočjo metode mrežastih tokov:

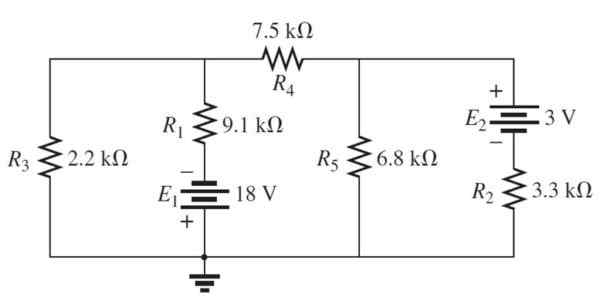Slika 4. 3 mrežasto vezje. Vir: Boylestad, r. 2011. Uvod v analizo vezja.2. mesto. Izdaja. Pearson.

Rešitev

Trije mrežasti tokovi so narisani, kot je prikazano na naslednji sliki, v poljubnih smiselnosti. Zdaj mrežice tečejo od koder koli:

Lahko vam služi: IMANTATION: Kaj je sestavljeno, metoda in primeri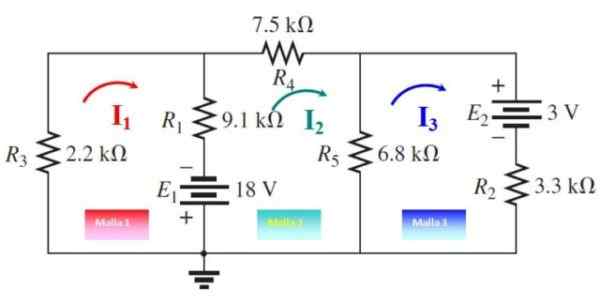 Slika 5. Mrežanski tokovi za vajo 2. Vir: f. Zapata, spremenjena iz Boylestada.

MRESA 1

-9100.Yo₁+18-2200.Yo₁+9100.Yo₂= 0

-11300 i₁ + 9100.Yo₂ = -18

MESH 2       

-(7500 +6800 +9100) .Yo₂ + 9100.Yo₁+6800.Yo₃-18 = 0

9100.Yo₁ - 23400.Yo₂ + 6800.Yo₃ = 18

MESH 3  

-(6800 + 3300) i₃ + 6800.Yo₂ - 3 = 0

6800.Yo₂ - 10100.Yo₃ = 3

Sistem enačb

-11300 i₁ + 9100.Yo₂ + 0.Yo₃= -18

9100.Yo₁ - 23400.Yo₂ + 6800.Yo₃ = 18

0.Yo₁ + 6800.Yo₂ - 10100.Yo₃ = 3

Čeprav so številke velike, se hitro reši s pomočjo znanstvenega kalkulatorja. Ne pozabite, da je treba enačbe naročiti in dodati ničle na mestih, kjer se neznano ne pojavlja, kot se pojavlja tukaj.

Mrežni tokovi so:

Yo₁ = 0.0012 a; Yo₂ = -0.00048 A; Yo₃ = -0.00062 a

Tokovi Yo₂ in Yo₃ Krožijo v nasprotni smeri na sliki, saj so se izkazali za negativne.

Tabela tokov in napetosti v vsakem uporu

Upor (ω)	Tok (amperi)	Napetost = i.R (volts)
9100	Yo1 -Yo2 = 0.0012-(-0.00048) = 0.00168	petnajst.3
3300	0.00062	2.05
2200	0.0012	2.64
7500	0.00048	3.60
6800	Yo2 -Yo3= -0.00048-(-0.00062) = 0.00014	0.95

Rešitev pravil Cramer

Ker so velike številke, je priročno uporabiti znanstvene zapise za neposredno sodelovanje z njimi.

Izračun i₁

Barvne puščice v determinantu 3 x 3 označujejo, kako najti številčne vrednosti in pomnožiti navedene vrednosti. Začnimo s pridobitvijo prvega razreda v determinantu δ:

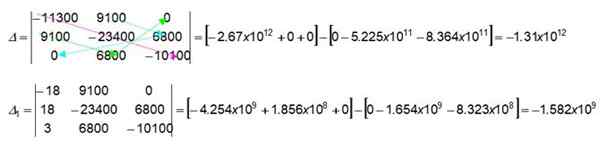
(-11300) x (-23400) x (-10100) = -2.67 x 10¹²

9100 x 0 x 0 = 0

9100 x 6800 x 0 = 0

Takoj dobimo drugi nosilec v isti determinanti, ki deluje od leve proti desni (za ta nosilec barvne puščice niso bile narisane na sliki). Bralca povabimo, da ga preveri:

0 x (-23400) x 0 = 0

9100 x 9100 x (-10100) = -8.364 x 10^enajst

6800 x 6800 x (-11300) = -5.225 x 10^enajst

Na enak način lahko bralec preveri tudi vrednosti za določitev Δ₁.

Pomembno: Med obema oklepama je vedno negativen znak.

Končno dobimo tok Yo₁ skozi Yo₁ = Δ₁ / Δ

Yo₁ = -1.582 x 10⁹/-1.31 x 10¹² = 0.0012 a                                   

Izračun i₂

Postopek lahko ponovite za izračun Yo₂, V tem primeru za izračun determinanta δ₂ Drugi stolpec determinanta δ se nadomesti s stolpcem neodvisnih izrazov in njena vrednost je v skladu z razloženim postopkom.

Vendar, kot je okorno zaradi velikega števila, še posebej, če ni znanstvenega kalkulatorja, je najpreprostejša nadomestiti vrednost Yo₁ že izračunano, v naslednji enačbi in jasno:

-11300 i₁ + 9100.Yo₂ + 0.Yo₃= -18 → 9100 i₂= -18 + 11300 i₁ → i₂ = -0.00048 a

I3 Izračun

Enkrat z vrednostmi Yo₁ in Yo₂ V roki Yo₃ Neposredno ga najdemo z zamenjavo.

Reference

1. Aleksander, c. 2006. Temelji električnega vezja. 3. mesto. Izdaja. MC Graw Hill.
2. Boylestad, r. 2011. Uvod v analizo vezja.2. mesto. Izdaja. Pearson.
3. Figueroa, d. (2005). Serija: Fizika za znanost in inženiring. Zvezek 5. Električna interakcija. Uredil Douglas Figueroa (USB).
4. Garcia, l. 2014. Elektromagnetizem. 2. mesto. Izdaja. Industrijska univerza v Santanderju.
5. Sears, Zemansky. 2016. Univerzitetna fizika s sodobno fiziko. 14. Ed. Zvezek 2.