Opredelitev centripetalnega pospeška, formule, izračun, vaje

The centripetalni pospešek do_c, Tudi radialni ali normalni, pri opisovanju krožne usmeritve nosi mobilni objekt. Njegova velikost je v²/r, kje r To je polmer kroga, usmerjen je proti njenemu središču in je odgovoren, da mobilni telefon ostane na svoji poti.

Dimenzije pospeševanja centripetalnega pospeška so dolžine na enoto. V mednarodnem sistemu so m/s². Če iz nekega razloga pospeševanje centripetala izgine, tako tudi moč, ki prisili mobilni telefon, da ohrani krožno usmeritev.

Vrkovalni predmeti imajo centripetalni pospešek, ki je usmerjen proti sredini poti. Vir: Pixabay

To se zgodi z avtomobilom, ki poskuša dati krivuljo na ravni in mraznem tiru, v kateri je trenje med tlemi in kolesi premalo, da avtomobil prevzame krivuljo. Zato je edina možnost, ki vam je ostala, premikanje po ravni črti in zato izstopite iz krivulje.

[TOC]

Krožni gibi

Ko se predmet premakne v krogu, je centripetalni pospešek radialno usmerjen proti sredini oboda, smeri, ki je pravokotna na sledi.

Ker je hitrost vedno tangentna za usmeritev, se tako hitrost in centripetalni pospešek izkažeta za pravokotno. Zato hitrost in pospešek nimata vedno iste smeri.

V teh okoliščinah ima mobilni telefon možnost opisovanja oboda s konstantno ali spremenljivo hitrostjo. Prvi primer je znan kot Uniform ali MCU krožno gibanje s svojo kratico, drugi primer pa bo spremenljivo krožno gibanje.

Lahko vam služi: kaj je brisanje emisij? (S primeri)

V obeh primerih je centripetalni pospešek odgovoren za ohranjanje mobilnega kroženja, ki zaseda, da se hitrost spreminja le v smeri in smeri.

Vendar pa bi bilo potrebno spremenljivo krožno gibanje, potrebna bi bila še ena komponenta pospeška v isti smeri hitrosti, ki je odgovorna za povečanje ali zmanjšanje hitrosti. Ta komponenta pospeška je znana kot Tangencialni pospešek.

Spremenljivo krožno gibanje in ukrivljeno gibanje na splošno imata tako sestavni deli pospeška, ker si lahko ukrivljeno gibanje predstavlja pot kot pot skozi nešteto obodov, ki sestavljajo ukrivljeno usmeritev.

Centripetalna sila

Zdaj je za zagotavljanje pospeška odgovorna sila. Za satelit, ki kroži po zemlji, je silo gravitacije. In ker gravitacija vedno deluje pravokotno na usmeritev, ne spreminja hitrosti satelita.

V tem primeru gravitacija deluje kot Centripetalna sila, Da ni poseben razred ali razen sile, ampak tisti, ki je v primeru satelita radialno usmerjen proti središču zemlje.

V drugih vrstah krožnega gibanja, na primer avtomobil, ki prevzame krivuljo, vlogo centripetalne sile razlagajo s statičnimi silami drgnjenja, ki sili mobilni telefon, da se obrne.

Formule za pospeševanje centripetala

Centripetalni pospešek se izračuna z izrazom:

Ac = v²/r

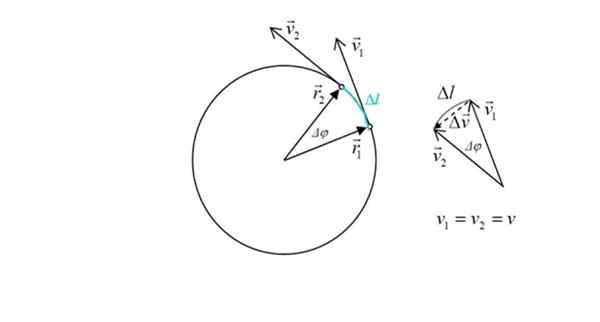Diagram za izračun centripetalnega pospeška v mobilnem telefonu z MCU. Vir: Vir: ilevanat [cc by-sa 3.0 (https: // creativeCommons.Org/licence/by-sa/3.0)]

Ta izraz bo sklenjen spodaj. Po definiciji je pospešek spreminjanje hitrosti v času:

Lahko vam služi: viri svetlobe: vrste in naprave, ki oddajajo svetlobo

Zgornji diagram prikazuje na levi sliki, dve točki, skozi katere prehaja mobilni telefon, ki se premika na radijskem krogu r V antihorarijskem smislu. Upoštevajte, da je velikost hitrosti v obeh primerih enaka, ne pa tudi smeri ali pomena.

Mobilni telefon uporablja čas δt Na turneji, ki je majhna, saj so točke zelo blizu.

Slika prikazuje tudi dva položajna vektorja r₁ in r₂, čigar modul je enak: radio r oboda. Kot med obema točkama je Δφ. V zeleni barvi priklon Ogled mobilnega telefona, označen kot ΔL.

Na sliki na desni je razvidno, da velikost δv, Sprememba hitrosti je približno sorazmerna z ΔL, saj je kot Δφ majhen. Toda sprememba hitrosti je natančno povezana s pospeševanjem. Trikotnik opozori z vsoto vektorjev, ki:

v₁ + Δv = v₂ → δv = v₂ - v₁

Δv Zanimivo je, saj je sorazmerno s centripetalnim pospeševanjem. Iz slike je opozorjeno, da je majhen kot Δφ, vektor Δv Je v pravokotnem bistvu v₁ kot v₂ in kaže na središče oboda.

Čeprav vektorji izstopajo krepko, za učinke geometrijske narave, ki sledijo, sodelujemo z moduli ali magnitudami teh vektorjev, ne glede na zapisovanje vektorja.

Nekaj ​​drugega: uporabiti morate definicijo osrednjega kota, kar je:

Δφ= Δl/r

Zdaj se primerjata obe številki, ki sta sorazmerna od kota δφ to je običajno:

Vam lahko služi: kaj je polarizirana svetloba?

 

Delitev med ΔT:

 Ker je po definiciji hitrosti v = Δl/ Δt. Toda δV/ Δt To je natančno velikost centripetalnega pospeška, kar je tisto, kar išče. Na ta način je dosežen izraz, opisan na začetku:

do_c= v²/r

Vaja rešena

Delček se premika v krogu 2.70 m radio. Ob določenem času je njegov pospešek 1.05 m/s² V smeri, ki naredi kot 32.0 ° z direktoratom za gibanje. Izračunajte svojo hitrost:

a) Takrat

b) 2.00 sekund kasneje, ob predpostavki stalnega tangencialnega pospeška.

Odgovor

Gre za raznoliko krožno gibanje, saj izjava kaže, da ima pospešek dani kot s smerjo gibanja, ki ni ali 0 ° (ne bi mogel biti krožno gibanje) ali 90 ° (to bi bilo enakomerno krožno gibanje).

Zato obe komponenti - radialni in tangencialni - soobstoječi. Bo označen kot_c že_t in videti narisano na naslednji sliki. Zeleni vektor je neto pospeški vektor ali preprosto pospeševanje do.

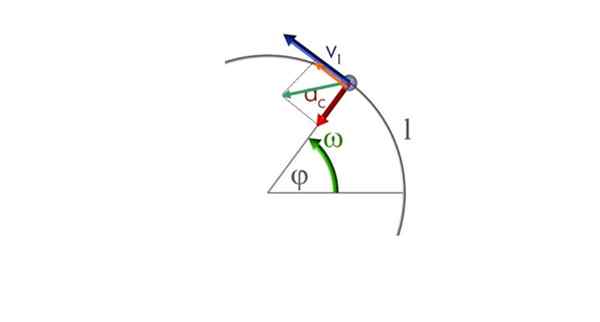Delec se v krožni poti premika v protihoralnem smislu in raznolikem krožnem gibanju. Vir: Commons.Wikimedia.org

a) Izračun komponent pospeška

do_c = a.cos θ = 1.05 m/s² . cos 32.0 ° = 0.89 m/s² (v rdeči barvi)

do_t = a.greh θ = 1.05 m/s² . Sen 32.0 ° = 0.57 m/s² (v oranžni)

Izračun mobilne hitrosti

Od a_c = v²/r, tako:
b) 2 sekundi kasneje hitrost v se bo povečal zahvaljujoč tangencialni komponenti pospeška

v = v_tudi +do_t. T = 1.6 m/s + (0.57 x 2) m/s = 2.74 m/s

Reference

1. Giancoli, d. Fizika. 2006. Načela z aplikacijami. Šesta izdaja. Dvorana Prentice. 107-108.
2. Hewitt, Paul. 2012. Konceptualna fizikalna znanost. Peta izdaja.Pearson.106 - 108.