Značilni vektorji enot, kako ga izvleči, primeri

The Vektorji enot so tisti, katerih modul, velikost ali velikost je enaka številčni vrednosti. Enotni vektorji so koristni za označevanje smeri drugih vektorjev, ki niso enote.

Spomnimo se, da so vektorji matematične entitete, ki matematično predstavljajo fizične velikosti, ki so odvisne od smeri, kot so moč, hitrost, pospešek in druge.

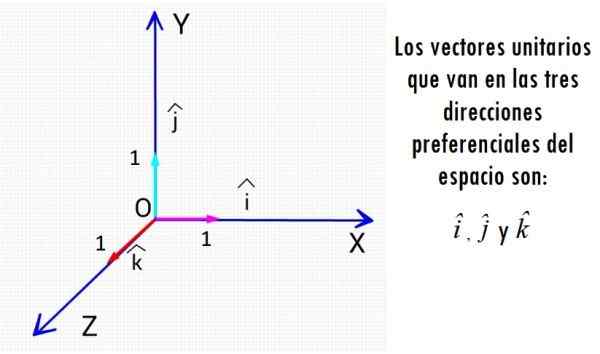
Najbolj znani enotni vektorji so trije vektorji, ki gredo v smeri kartezijanskih osi. Vir: f. Zapata.

Ne glede na fizično velikost, ki je povezana.

Na primer, hitrost delca, ki se premika pri 3 m/s in gre v pozitivno smer kartezijanske osi X, je označena: v = (3 m/s) Yo, kjer se drzna črka uporablja za označevanje vektorskih zneskov. V tem primeru modul v Je 3 m/s in vektorski modul enote Yo je 1 (brez enot).

[TOC]

Modul, smer in pomen

Glede na pomembno. V času predstavljanja vektorskega zneska je treba jasno navesti te vidike.

Zdaj ima lahko vektor enote poljubno smer in pomen, ki je prednostna, vendar mora biti velikost vedno enaka 1.

Vektorji enot se uporabljajo za označevanje zasebnega naslova v prostoru ali v ravnini. Če moramo na primer delati z vsemi silami, ki delujejo vzdolž vodoravne osi, saj nam enotni vektor v tej smeri pomaga razlikovati te sile od drugih, usmerjenih v drugo smer.

In da jih ločimo od vektorjev, ki niso enote, se krepko običajno uporablja pri tisku in na primer postavite naglas Circumflex, na primer:

Lahko vam služi: stacionarna teorija države: zgodovina, razlaga, novice

Za ročno napisana besedila je dovolj, da postavimo Circusflejo, da razumemo, da gre za enotni vektor.

Značilnosti enotnega vektorja

Matematično vektor enote:

Gre za element, ki spada v vektorski prostor ℛ dimenzije n, tako da |v| = 1, kjer palice pomenijo "modul".

Tako lahko to ugotovimo:

-Enotni vektorski modul je vedno 1, ni pomembno, ali gre za moč, hitrost ali drug vektor.

-Enotni vektorji imajo določeno smer, pa tudi smer, na primer vektor enote v navpični smeri, ki je lahko smiselna navzgor ali navzdol.

-Enotni vektorji imajo izvorno točko. Če ga predstavlja kartezijanski koordinatni sistem, omenjena točka sovpada z izvorom sistema: (0,0), če je ravnina ali (0,0,0), če je vektor v tri -dimenzionalnem prostoru.

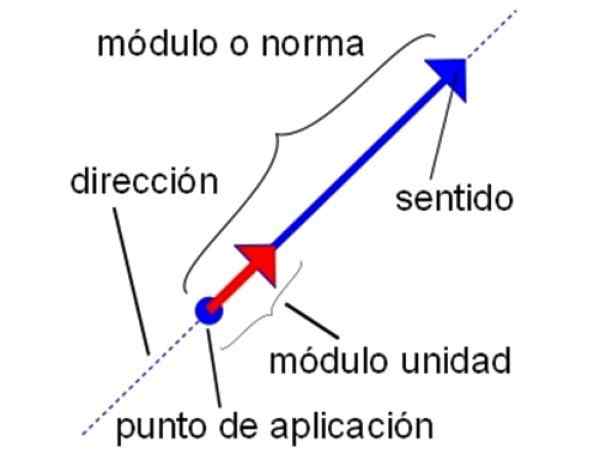Značilnosti vektorja enote. Vir: Wikimedia Commons.

-Tudi z enotnimi vektorji lahko izvedemo vse operacije vsote, odštevanja in množenja vektorjev, ki jih izdelujejo redni vektorji. Zato je veljavno pomnožiti enotni vektor s skalarnim, pa tudi izvesti točkovni izdelek in navzkrižni izdelek.

-Z enotnim vektorjem v določeni smeri se lahko izrazijo tudi drugi vektorji, ki so tudi v tej smeri usmerjeni.

Vektorji enot v vesolju

Če želite izraziti kateri koli vektor v prostoru ali v ravnini. Vsaka od treh preferencialnih smeri prostora ima svoj vektor enote.

Vrnimo se na primer sil, usmerjenih vzdolž vodoravne osi. To je os x, ki ima dve možnosti: smer na desno in smer v levi. Recimo, da je na osi x enotni vektor in usmerjen v desno, ki ga lahko označimo skozi katero koli od teh oblik:

Vam lahko služi: Thomson Atomski model: značilnosti, postulati, subatomski delci

Vsak od njih je veljaven. Zdaj, predpostavimo, da silo F₁ Magnitude 5 N vzdolž te osi in usmerjene v desno, takšno silo bi lahko izrazili kot:

Če bi bila sila usmerjena vzdolž osi x, vendar v nasprotni smeri, to je levo, bi lahko za določitev te razlike uporabili negativni znak.

Na primer, 8 n sila, ki se nahaja na osi x in usmerjena na levo, bi bila takšna:

Ali tako:

In za vektorje, ki niso usmerjeni vzdolž kartezijanskih osi, obstaja tudi način, kako jih predstavljati v smislu vektorjev ortogonalne enote, prek kartezijanskih komponent.

Kako odstraniti/izračunati vektor enote?

Za izračun enotnega vektorja v smeri katerega koli poljubnega vektorja v, Uporabljena je naslednja formula:

Kje:

Je modul ali velikost vektorja v, čigar kvadrat se izračuna tako:

|v|² = (v_x)² +  (v_in)²+  (v_z)²

Poljubni vektor v smislu vektorja enote

Alternativno vektor v Lahko se izrazi na naslednji način:

To pomeni, da je produkt njegovega modula z ustreznim vektorjem enote. Točno to je bilo storjeno prej, ko govorimo o sili 5 N, usmerjene vzdolž pozitivne osi X.

Grafični prikaz

Grafično, kar je rečeno na tej sliki, kjer je vektor v Je v modri barvi in ​​ustrezen vektor enote v svoji smeri je v rdeči barvi.

V tem primeru vektor v Ima velikost večjo kot pri vektorju enote, vendar je razlaga celo veljavna, če se to ne zgodi. Z drugimi besedami, lahko imamo vektorje, ki so na primer 0.25 -krat večji vektor enote.

Vam lahko služi: teža (fizična): izračun, enote, primeri, vaje

Primeri enotnih vektorjev

Vektorji pravokotne enote I, J in K

Kot smo že videli, vektorji pravokotne enote Yo, J in k Zelo so koristni za predstavljanje katerega koli drugega vektorja v ravnini ali prostoru in izvajati vektorske operacije. Glede na omenjeni vektor je poljubni vektor V predstavljen kot:

v = v_x Yo + v_in J + v_z k

Kjer v_x, v_in in v_z so pravokotne sestavine vektorja v, ki so vzponi -Bold, se ne uporabljajo za predstavljanje v tiskanem besedilu-.

Coulombov zakon

Enotni vektorji se pogosto pojavljajo v fiziki. Tam imamo na primer Coulombov zakon, ki kvantitativno opisuje interakcijo med dvema specifičnimi električnimi naboji.

Kaže, da je sila F privlačnosti ali odbojnosti med temi obremenitvami je sorazmerna z njihovimi produkt, obratno sorazmerna s kvadratom razdalje, ki jih loči in je usmerjena v smeri vektorja enote, ki se pridruži obremenitvam.

Ta vektor je običajno predstavljen z:

In Coulombov zakon je tak, v vektorski obliki:

Kje k To je elektrostatična konstanta, q₁ in q₂ So obremenitve in r Razdalja jih loči.

Vaja rešena

Poiščite enoto vektorja v smeri vektorja v = 5Yo + 4J -8k, Dano v poljubnih enotah.

Rešitev

Zgoraj je uporabljena opredelitev enotnega vektorja:

Najprej pa morate izračunati vektorski modul, ki kot ima tri komponente, določeno z:

|v|² = (v_x)² +  (v_in)² +  (v_z)²

Ostati:

|v|² = (5)² +  (4)² +  (-8)²= 25 + 16 + 64 = 105

Zato modul v je:

|v| = √105

Iskani enotni vektor je preprosto:

To nas končno pripelje do:

v = 0.488 Yo + 0.390 J - 0.781 k

Reference

1. Bauer, w. 2011. Fizika za inženiring in znanosti. Zvezek 1. MC Graw Hill.
2. Bedford, 2000. Do. Mehanika za inženiring: statična. Addison Wesley.
3. Figueroa, d. (2005). Serija: Fizika za znanost in inženiring. Zvezek 1. Kinematika. Uredil Douglas Figueroa (USB).
4. Giambattista, a. 2010. Fizika. 2. mesto. Ed. McGraw Hill.
5. Resnick, r. (1999). Fizično. Vol. 1. 3. izd. v španščini. Continental uredništvo s.Do. od c.V.