Vertikalne formule za streljanje, enačbe, primeri

On navpično streljanje To je gibanje, ki poteka pod delovanjem polja sil, običajno v gravitaciji, ki se lahko vzpenja ali pada. Znano je tudi po imenu Navpični zagon.

Najbolj neposreden primer je vrženo (ali navzdol, če je prednostno) kroglico z roko, da, poskrbite, da bo to storilo navpično. Preziba zračne odpornosti, gibanje, ki sledi krogli, se popolnoma prilega enakomerno raznolikemu pravokotnemu gibanju (MRUV).

Slika 1. Govoriti z žogo navpično navzgor je dober primer navpičnega posnetka. Vir: Pexels.

Vertikalno streljanje je široko preučeno gibanje v uvodnih tečajih fizike, saj je vzorec gibanje v dimenziji, Zelo preprost in uporaben model.

Ta model ni mogoče uporabiti le za preučevanje kinematike predmetov pod delovanjem gravitacije, ampak tudi, kot bo razvidno iz pozneje, opisuje gibanje delcev na sredini enotnega električnega polja.

[TOC]

Formule in enačbe

Prva stvar, ki je potrebna, je koordinatni sistem, ki označuje izvor in ga označi s črko, ki je v primeru navpičnih gibanj črka "in".

Potem je izbran pozitiven smisel +in, ki je običajno gor in pomen -in ki se običajno odstrani (glej sliko 2). Vse to, razen če kdo reši problem, ne odloči drugače, saj je druga možnost, da se tako pozitivno sprejmejo v smer gibanja, ne glede na to.

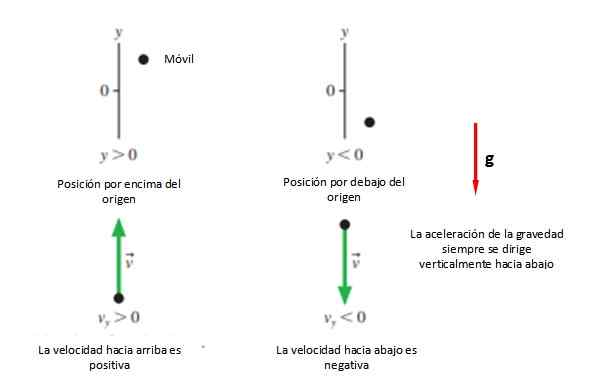Slika 2. Običajna konvencija znakov v navpičnem posnetku. Vir: f. Zapata.

Vsekakor je priporočljivo, da izvor sovpada s točko predstavitve in_tudi, Ker so enačbe poenostavljene, čeprav lahko zaženete katero koli želeno stališče, da začnete preučevati gibanje.

Lahko vam služi: drugo ravnotežno stanje: razlaga, primeri, vaje

Vertikalne enačbe streljanja

Ko sta koordinatna sistem in izvor vzpostavljena, gremo do enačb. Velike, ki opisujejo gibanje, so:

-Začetna hitrost v_tudi

-Pospešek do

-Hitrost v

-Začetni položaj x_tudi

-Položaj x

-Premik Dx

-Čas t

Vsi razen časa so vektorji, a ker gre za eno -dimenzionalno gibanje z določeno smerjo, kar je pomembno, uporablja znake + ali. V primeru navpičnega streljanja se gravitacija vedno spusti in, če ni drugače določeno, se dodeljuje znak -.

Takrat obstajajo enačbe, prilagojene za navpično streljanje, ki nadomeščajo "x"in"In"do"g". Poleg tega znak (-), ki ustreza gravitaciji, usmerjeni navzdol:

1) položaj: y = y_tudi + v_tudi.T - ½ g.t²

2) Hitrost: v = v_tudi - g.t

3) Hitrost, odvisno od premika δin: v² = v_tudi² - 2.g. Δin

Primeri

Potem obstajajo primeri prijave za navpično fotografiranje. V svoji resoluciji je treba upoštevati naslednje:

-"g"Ima konstantno vrednost, da je v povprečju 9,8 m/s² ali približno 10 m/s² Če je raje olajšati izračune, kadar ni potrebna preveč natančnost.

-Kdaj v_tudi v redu 0, Te enačbe so zmanjšane na tiste prosti pad.

-Če je lansirna. Ko je v gibanju, predmet doseže največjo višino, ki bo odvisna od tega, kako velika je začetna hitrost. Seveda do večje višine bo mobilni telefon preživel več časa v zraku.

-Predmet se vrne na izhodišče z enako hitrostjo, s katero je bil sprožen, vendar je hitrost usmerjena navzdol.

-Za navpično zagon, višja kot je začetna hitrost, prej bo predmet prišel na tla. Tu je prevožena razdalja pritrjena glede na izbrano višino za zagon.

Vam lahko služi: kaj je relativno in absolutno hrapavost?

-V navpičnem posnetku se čas, ki doseže največjo višino, izračuna čas, ki potrebuje mobilno v = 0 V enačbi 2) prejšnjega razdelka. To je največji čas t_Max:

0 = v_tudi - g . t_Max ⇒ t_Max = v_tudi /g

-The največja višina in_Max Razjasni iz enačbe 3) tudi prejšnjega oddelka v = 0:

0 = v_tudi² - 2.g. Δy ⇒ 0 = V_tudi² - 2.g. (in_Max - in_tudi) ⇒ in_Max = y_tudi  + v_tudi² / 2 g

Ja in_tudi = 0, Zmanjša se na:

in_Max = v_tudi² / 2 g

Rešen primer 1

Žoga z V se vrže navpično navzgor_tudi = 14 m/s, z vrha 18 m visoke stavbe. Žoga je dovoljena, da sledi svojemu nižje do pločnika. Izračunati:

a) Največja višina, ki jo doseže žoga glede na tla.

b) čas v zraku (čas letenja).

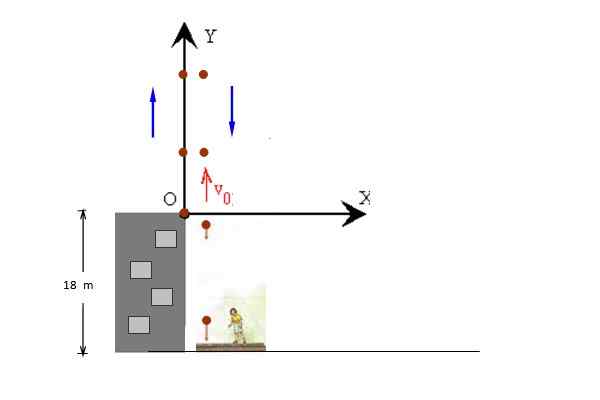Slika 3. Žoga se vrže navpično s strehe stavbe. Vir: f. Zapata.

Rešitev

Na sliki se gibi naraščanja in spuščanja kroglice pojavijo ločeno zaradi jasnosti, vendar se oba zgodita po isti črti. Začetni položaj je zavzet pri y = 0, tako da je končni položaj y = - 18 m.

a) Največji ukrep, izmerjen s strehe stavbe in_Max = v_tudi² / 2 g In iz izjave je razvidno, da je začetna hitrost +14 m/s, potem pa:

in_Max = (14 m/s)² / 2 x 9.8 m/s² = 10 m (Glede strehe)

H_Max = 10 m + 18 m = 28 m (Glede pločnika).

b) najti Skupni čas tudi čas letenja Če v zraku traja, bo uporabila enačbo y = y_tudi + v_tudi.T - ½ g.t², Z naslednjimi vrednostmi in znaki:

y = - 18 m

in_tudi = 0 m

v_tudi = +14 m/s

Zamenjava:

- 18 = 14.T - ½ 9.8 .t²

- 4.9 T²+14.T + 18 = 0 

4.9 T²-14.T - 18 = 0

To je enačba drugega stopinj, ki jo je enostavno rešiti s pomočjo znanstvenega kalkulatorja ali z uporabo ločljivosti. Rešitve so: 3.82 in -0.96. Negativna rešitev je zavržena, saj čas nima fizičnega pomena.

Lahko vam služi: toplota: formule in enote, značilnosti, kako se meri, primeri

Čas letenja žoge je 3.82 sekund.

Rešen primer 2

Pozitivno obremenjen delček z Q = +1.2 Milicoulombs (MC) in masa M = 2.3 x 10 ^-10 Kg Projicira se navpično navzgor, začenši od položaja, prikazanega na sliki, in z začetno hitrostjo v_tudi = 30 km/s.

Med naloženimi ploščami je električno polje In Enotna, usmerjena navpično navzdol in velikost 780 n/c. Če je razdalja med ploščami 18 cm, se bo delček trčil v zgornjo ploščo? Prezirajte gravitacijsko privlačnost na delcu, saj je izjemno lahka.

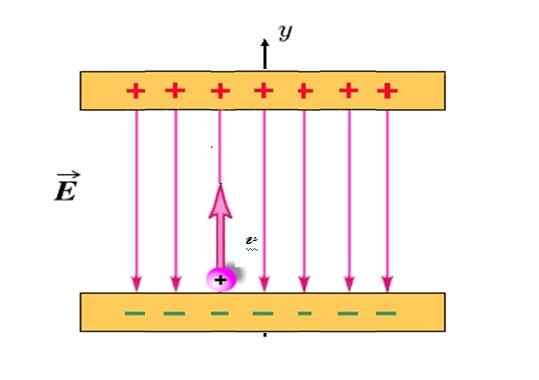Slika 4. Pozitivni delček obremenitve se premika podobno kot kroglica, vržena navpično navzgor, ko je potopljena v električno polje slike. Vir: Spremenjeno s F. Čevelj Wikimedia Commons.

Rešitev

V tej težavi električno polje In je tisti, ki ustvarja silo F in posledično pospeševanje. Ker je pozitivno obremenjen, delček vedno privlači spodnjo ploščo, vendar, ko ga projiciramo navpično navzgor.

Po definiciji električnega polja:

E = f/q = m.A /Q ⇒ a = q.E / m

Pred zamenjavo vrednosti je treba uporabiti to enakovrednost:

1 mc = 1 x 10^-3 C

S tem je pospešek:

A = 1.2 x 10^-3 X 780 /2.3 x 10 ^-10gospa² = 4.07 x 10⁹ gospa²

Za največjo višino se uporablja formula prejšnjega odseka, vendar namesto uporabe “g"Ta vrednost pospeška se uporablja:

in_Max = v_tudi² / 2a = (30.000 m/s)²/2 x 4.07 x 10⁹ gospa² = 0.11 m = 11 cm

Ne trčite v zgornjo ploščo, saj je od izhodišča 18 cm, delček pa takoj, ko dvigne 11 cm.

https: // youtu.Biti/kt08ntudzwq

Reference

1. Kirkpatrick, l. 2007. Fizika: pogled na svet. 6^ta Skrajšana izdaja. Cengage učenje. 23 - 27.
2. Rex, a. 2011. Osnove fizike. Pearson. 33 - 36
3. Sears, Zemansky. 2016. Univerzitetna fizika s sodobno fiziko. 14^th. Ed. Zvezek 1. 50 - 53.
4. Serway, r., Vulle, c. 2011. Osnove fizike. 9^na Ed. Cengage učenje. 43 - 55.
5. Wilson, J. 2011. Fizika 10. Pearson Education. 133 - 149.