Značilnosti paraboličnega posnetka, formule in enačbe, primeri

On Parabolični strel Sestavljen je iz metanja predmeta ali izstrelke z določenim kotom in ga pustite, da se premika pod delovanjem gravitacije. Če se zračna odpornost ne upošteva, bo predmet, ne glede na njegovo naravo, sledil poti v obliki parabole.

To je vsakodnevno gibanje, saj med najbolj priljubljenimi športi so tisti, v katerih se kroglice ali kroglice vržejo z roko, z stopalom ali z instrumentom, kot je lopar ali palico.

Slika 1. Vodni curek iz okrasnega vira sledi parabolični poti. Vir: Wikimedia Commons. Zátonyi Sandor (ifj.),, Fizped/CC by-SA (https: // creativeCommons.Org/licence/by-sa/3.0

Za študijo je parabolični posnetek razdeljen na dva prekrivajoča se gibanja: eno vodoravno brez pospeška, drugi pa navpični s konstantnim pospeševanjem, kar je gravitacija. Oba gibanja imata začetno hitrost.

Recimo, da vodi vodoravno gibanje. Vsak od teh gibanj je neodvisen od drugega.

Glede na to, da je določitev položaja izstrelkov glavni cilji, je treba izbrati ustrezen referenčni sistem. Podrobnosti so naslednje.

[TOC]

Formule in enačbe paraboličnega posnetka

Recimo, da se objekt vrže s kotom α glede na vodoravno in začetno hitrost v_tudi kot je prikazano na spodnji sliki na levi strani. Parabolični posnetek je gibanje, ki poteka na letalu Xy In v tem primeru se začetna hitrost razpade tako:

v_vol = v_tudi cos α

v_Oy = v_tudi greh α

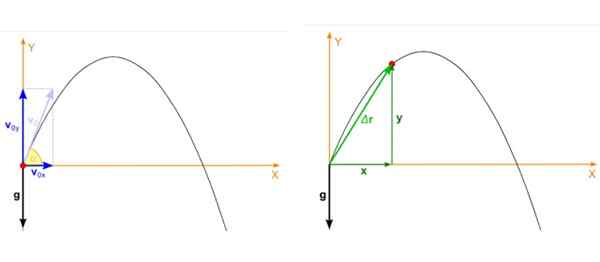Slika 2. Na levi strani začetna hitrost izstrelitve in na desni položaj v vsakem trenutku predstavitve. Vir: Wikimedia Commons. Zátonyi Sandor, (ifj.) Fizped/CC by-SA (https: // createCommons.Org/licence/by-sa/3.0.

Položaj izstrelkov, ki je rdeča točka na sliki 2, desna slika, ima tudi dve komponenti, ki sta odvisna od časa, eno v x In drugi v in. Položaj je vektor, ki je označen kot r in njene enote so dolžine.

Vam lahko služi: Isomeria

Na sliki začetni položaj projektila sovpada z izvorom koordinatnega sistema, torej x_tudi = 0, in_tudi = 0. To ni vedno tako, izvor je mogoče izbrati kjer koli, vendar ta izbira veliko poenostavi.

Kar zadeva dva gibanja v X in Y, sta to:

-X (t): gre za enotno pravokotno gibanje.

-in (t): ustreza enakomerno pospešenemu pravokotnemu gibanju z g = 9.8 m/s² in usmerjanje navpično navzdol.

V matematični obliki:

x (t) = v_tudi cos α.t

in (t) = v_tudi .greh α.T - ½G.t²

Vektor položaja ostaja:

r (t) = [v_tudi cos α.T]Yo + [v_tudi .greh α.T - ½G.t²] J

V teh enačbah bo pozorni bralec opazil, da je znamenje minus posledica dejstva, da resnost kaže na tla, smisel, ki je bil izbran kot negativen, medtem ko je navzgor jet kot pozitiven.

Ker je hitrost prvi izhaja iz položaja, je dovolj za izpeljavo r (t) glede na čas in pridobite:

v (t) = v_tudi cos α Yo + (v_tudi .greh α - Gt) J

Končno je pospešek izražen vektorsko kot:

do (t) = -g J

- Usmeritev, največja višina, največji čas in vodoravni doseg

Usmeritev

Če želite najti izrecno enačbo poti, ki je krivulja y (x), morate odpraviti časovni parameter, čiščenje v enačbi za x (t) in nadomestiti v y (t). Poenostavitev je nekoliko naporna, vendar je končno pridobljena:

Največja višina

Največja višina se pojavi, ko v_in = 0. Vemo, da obstaja naslednje razmerje med položajem in kvadratom hitrosti:

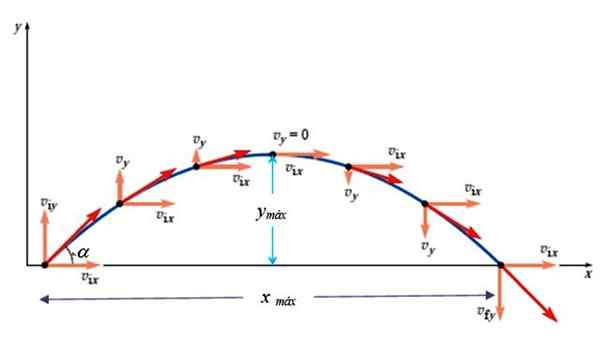Slika 3. Hitrost v paraboličnem posnetku. Vir: Giambattista, a. Fizika.

v_in² = v_Oy ²- 2Gy

Delati v_in = 0 ravno takrat, ko doseže največjo višino:

0 = v_Oy ²- 2 g.in_Max → in_Max = v_Oy ²/2 g

Z:

Vam lahko služi: centripetalni pospešek: definicija, formule, izračun, vaje

v_Oy = v_tudi Senα

Največji čas

Največji čas je čas, ki ga objekt vzame za dosego in_Max. Za izračun se uporablja:

v_in = v_tudi .greh α - Gt

Vedeti to v_in To je končano 0, ko t = t_Max, rezultat:

v_tudi .greh α - g.t_Max = 0

t_Max = v_Oy /g

Največji horizontalni razpon in čas letenja

Obseg je zelo pomemben, saj kaže, kje bo objekt padel. Torej bomo vedeli, ali to daje belo ali ne. Da bi ga našli, potrebujemo čas letenja, skupni čas ali t_v.

Od prejšnje ilustracije je enostavno sklepati t_v = 2.t_Max. Toda pozornost je resnična le, če je izstrelitev na ravni, to je višina izhodišča enaka višini prihoda. V nasprotnem primeru je čas reševanja enačbe druge stopnje, ki je posledica nadomestitve končnega položaja in_finale:

in_finale = v_tudi .greh α.t_v - ½g.t_v²

Vsekakor je največji vodoravni obseg:

x_Max = v_vol. t_v

Primeri paraboličnega streljanja

Parabolični posnetek je del gibanja ljudi in živali. Tudi skoraj vseh športov in iger, kjer se gravitacija posreduje. Na primer:

Parabolično streljanje v človeških dejavnostih

-Kamen, ki ga je vrgel katapult.

-Kratka vratarja.

-Žoga, ki vrže vrč.

-Puščica, ki pride iz loka.

-Vse vrste skokov

-Vrzi kamen.

-Kakršno koli metanje orožja.

Slika 4. Kam. Vir: Wikimedia Commons.

Parabolični strel v naravi

-Voda, ki izvira iz naravnih ali umetnih curkov, kot so vir.

-Kamni in lava, ki izvirajo iz vulkana.

-Kroglica, ki odskoči na pločniku ali kamnito, ki jo naredi na vodi.

-Vse vrste živali, ki skačejo: kenguruji, delfini, gazelle, mačke, žabe, zajci ali žuželke, če omenjam nekaj.

Lahko vam služi: mehanska moč: kaj je, aplikacije, primeriSlika 5. Impala lahko skoči do 3 m. Vir: Wikimedia Commons. Arturo de frias marques/cc by-s-s (https: // createCommons.Org/licence/by-sa/3.0.

Vaja

Kobilica, ki tvori kot 55 ° z vodoravnim in pristane na 0.80 metrov kasneje. Najti:

a) dosežena največja višina.

b) Če bi skočil z enako začetno hitrostjo, vendar bi oblikoval kot 45 °?

c) Kaj lahko rečemo o največjem horizontalnem dosegu za ta kot?

Rešitev

Kadar podatki, ki jih ponuja težava, ne vsebujejo začetne hitrosti V_tudi Izračuni so nekoliko bolj naporni, toda iz znanih enačb je mogoče sklepati nov izraz. Začeti od:

x_Max = v_vol . t_let = v_tudi.cos α. t_v

Ko pristane kasneje, je višina spet 0, nato pa:

v_tudi .greh α.t_v - ½g.t_v²= 0

Kot t_v To je pogost dejavnik, poenostavljen je:

v_tudi .greh α - ½g.t_v= 0

Lahko razčistimo t_v Iz prve enačbe:

t_v = x_Max / v_tudi.cos α

In zamenjajte v drugem:

v_tudi .greh α - (½g.x_Max / v_tudi.cos α) = 0

Z množenjem vseh izrazov do v_tudi.cos αIzraz se ne spreminja in imenovalec izgine:

(v_tudi .greh α.) (v_tudi.cos α) - ½g.x_Max = 0

v_tudi² greh α. cos α = ½g.x_Max

Je že mogoče očistiti v_tudi Ali pa tudi nadomestite naslednjo identiteto:

Sen 2α = 2 sen α. cos α → V_tudi² Sen 2α = g.x_Max

Se izračuna v_tudi²:

v_tudi² = g.x_Max / Sen 2α = (9.8 x 0.8 / sen 110) m²/s² = 8.34 m²/s²

In končno največja višina:

in_Max= v_Oy ²/2G = (8.34 X Sen² 55)/(2 x 9.8) M = 0.286 M = 28.6 cm

Rešitev b

Jastoga uspe ohraniti enako vodoravno hitrost, ko pa se kot zmanjšuje:

in_Max= v_Oy ²/2G = (8.34 X Sen² 45)/(2 x 9.8) M = 0.213 M = 21.3 cm

Doseže manjšo višino.

Rešitev c

Največji vodoravni obseg je:

x_Max = v_tudi² Sen 2a / g

Ko se kot spreminja, se spremeni tudi vodoravni obseg:

x_Max = 8.3. 4 Sen 90 / 9.8  M = 0.851 M = 85.1 cm

Skok je zdaj daljši. Bralec lahko preveri, ali je največ za kota 45 °:

sin 2α = sin 90 = 1.

Reference

1. Figueroa, d. 2005. Serija: Fizika za znanost in inženiring. Zvezek 1. Kinematika. Uredil Douglas Figueroa (USB).
2. Giambattista, a. 2010. Fizika. Druga izdaja. McGraw Hill.
3. Giancoli, d.  2006. Fizika: načela z aplikacijami. 6. Ed Prentice Hall.
4. Resnick, r. 1999. Fizično. Vol. 1. 3. izd. v španščini. Continental uredništvo s.Do. od c.V.
5. Sears, Zemansky. 2016. Univerzitetna fizika s sodobno fiziko. 14. Ed. Zvezek 1.