Tretji zakon formul termodinamike, enačbe, primeri

The Tretji zakon termodinamike navaja, da je entropija zaprtega termodinamičnega sistema v ravnotežju ponavadi minimalna in konstantna, saj se njegova temperatura približa 0 Kelvinu.

Ta vrednost entropije bo neodvisna od spremenljivk sistema (med drugim tlak ali uporabljeno magnetno polje). Kar se zgodi, je, da se temperatura bliža 0 K, procesi v sistemu se ustavijo in kako je entropija merilo notranje vznemirjenosti, se nujno spusti.

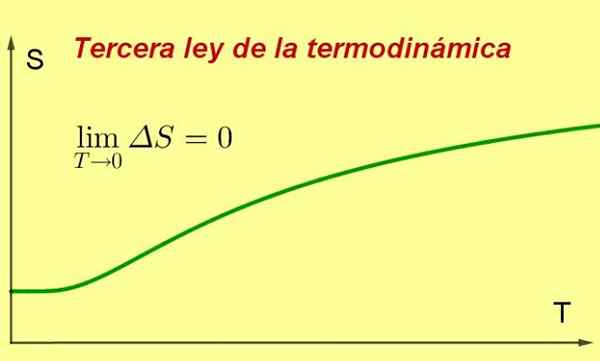
Slika 1. Ko se temperatura sistema približa absolutni ničli, njegova entropija doseže minimalno in konstantno vrednost. Vir: Pripravil F. Zapata ..

[TOC]

Prejšnji koncepti

Če želite razumeti obseg tretjega zakona termodinamike, ki je pomemben za zelo nizke temperature, je treba pregledati naslednje koncepte:

Termodinamični sistem

Običajno se nanaša na plin, tekočino ali trdno snov. Kar ni del sistema, se imenuje okoli. Najpogostejši termodinamični sistem je idealen plin, ki ga sestavljajo N delci (atomi), ki medsebojno delujejo le z elastičnimi trki.

Izolirani, zaprti ali odprti sistemi

Izolirani sistemi niso dovoljeni nobeni izmenjavi z okoljem. Zaprti sistemi ne izmenjujejo snovi z okoljem, ampak toploto. Končno lahko odprti sistemi izmenjujejo tako materijo kot toploto z okoljem.

Makro -stanja in mikrostata

Makrostati sistema je niz vrednosti, ki imajo njegove spremenljivke: tlak, temperatura, prostornina, število molov, entropija in notranja energija. Po drugi strani pa mikro -esteem -v primeru idealnega plina, ki ga daje položaj in zagon vsakega od n delcev, ki ga sestavljajo, v določenem trenutku. 

Številne mikrostate lahko povzročijo isti makrostati. V plinu pri sobni temperaturi je število možnih mikrostatov neizmerno, saj je število delcev, ki jih sestavljajo, različni položaji in različne energije, ki jih lahko sprejmejo. 

Formule in enačbe

Entropija, kot smo rekli, je termodinamična makroskopska spremenljivka, ki meri sistem molekulske motnje sistema. Stopnja motnje sistema je večja do te mere, da je število možnih mikrostat večje. 

Ta koncept je potreben za oblikovanje tretjega zakona termodinamike v matematični obliki. Naj bo to entropija sistema, potem:

To pomeni, da se entropija S v zaprtem sistemu ne spremeni, ko se njegova temperatura T nagnila k absolutni ničli.

Entropija je makroskopsko spremenljivko stanja, ki je neposredno povezana s številom možne mikrostate sistema s pomočjo naslednje formule:

S = k ln (w)

V prejšnji enačbi: S predstavlja entropijo, W število možnih mikrostat sistema in k To je Boltzmannova konstanta (K = 1.38 x 10^-23 J/k). To pomeni, da je entropija sistema k večji naravni logaritem števila možnih mikrostat.

Izračun absolutne entropije snovi

Možno je določiti absolutno entropijo čiste snovi, ki temelji na definiciji variacije entropije:

Kjer je ΔQ neskončno majhna variacija toplote in t je temperatura. Ta enačba je veljavna, če je postopek reverzibilen (Rev).Če gre za izobarični postopek s konstantnim tlakom, se lahko toplota, izmenjena med neskončno majhno temperaturno nihanje, zapisati tako:

ΔQ = n . c_str .Dt

Tu je CP specifična molarna toplota in n število molov. Molarna specifična odvisnost toplote s temperaturo je eksperimentalno dobljeno dejstvo in znana za številne čiste snovi.

Vam lahko služi: sončni sistem: planeti, značilnosti, izvor, evolucija

V skladu s tretjim zakonom v čistih snovi: 

Torej absolutna entropija mola čiste snovi, kot je:

V prejšnjem zapisu palica kaže, da gre.

Prijave

V vsakdanjem življenju ima tretji zakon termodinamike malo aplikacij, v nasprotju s prvim in drugim zakonom. To je zato, ker gre za načelo, ki se nanaša na to, kar se dogaja v sistemu, ko se približa absolutnemu 0, rang redkih temperatur.

Pravzaprav je doseganje absolutnega ali −273,15 ° C nemogoče (glej primer 1 kasneje), vendar se tretji zakon uporablja pri preučevanju odziva materialov pri zelo nizkih temperaturah. 

Zahvaljujoč temu se je pojavil pomemben napredek v zgoščeni snovi, na primer:

-Presežek (glej primer 2 kasneje)

-Superprevodnost 

-Tehnike laserskega hlajenja 

-Bose-Einstein kondenzat 

-Fermi odvečni plini.

Slika 2. Odveč tekoči helij. Vir: Wikimedia Commons.

Pri izjemno nizkih temperaturah spust entropije omogoča nastanek zanimivih kvantnih pojavov. Zato poglejmo, kaj se zgodi z entropijo zelo nizko temperaturnega sistema.

Entropija nizkocenodnega sistema

Ko imate popolno kristalno snov, je njegova minimalna entropija točno nič, saj je zelo urejena. Pri temperaturah, ki so blizu absolutnega 0, je snov v kondenziranem stanju (tekoča ali trdna), steklene vibracije pa so minimalne.

Nekateri avtorji menijo, da je alternativna izjava tretjega zakona termodinamike naslednja:

"Če je snov kondense, ki tvorijo popoln kristal, ko se temperatura nagiba k absolutni ničli, se entropija nagiba natančno na ničlo". 

Dokončno oglejte nekatere vidike prejšnje izjave: 

- Popoln kristal je tisti, v katerem je vsaka molekula enaka in v katerem se molekularna struktura ponavlja v celoti.

- Ker se temperatura absolutno ničla, se atomske vibracije skoraj popolnoma zmanjšajo.

Potem steklo tvori enotno možno konfiguracijo ali mikro -postave, to je W = 1, In zato je entropija enaka nič:

 S = k ln (1) = 0

Toda ne toliko časa, kolikor je material, ohlajen blizu absolutne ničle, tvori kristal, še manj je ta kristal popoln. To se zgodi le, če je postopek hlajenja zelo počasen in reverzibilen.

V nasprotnem primeru bi dejavniki, kot so nečistoče v kozarcu, omogočili obstoj drugih mikrostat. Zato bi bila w> 1 in entropija večja od 0.

Preostala entropija

Če je postopek hlajenja nagnjen, sistem med isto zaporedje neenakomernih stanj, kar vodi v gradivo. V tem primeru ni kristalne in urejene strukture, ampak amorfna trdna snov, katere struktura je podobna strukturi tekočine. 

V tem primeru najmanjša vrednost entropije v bližini absolutne ničle ni nič, saj je število mikrostat veliko večje od 1. Razlika med to entropijo in ničelno entropijo popolnega kristalnega stanja je znana kot Preostala entropija.

Pojasnilo je, da sistem pod določeno pragovno temperaturo nima druge možnosti kot zasedba.

Lahko vam služi: prvi zakon termodinamike: formule, enačbe, primeri

Odgovorni bodo za ohranjanje stalne entropije, tudi če se temperatura še naprej spušča proti absolutni ničli.

Primeri

Primer 1: Absolutna nič in nedoločitev Heisenberga

Načelo nedoločenja Heisenberga določa, da negotovost v položaju in zagonu delca, na primer v atomih kristalne mreže, niso neodvisna od druge, vendar sledite naslednji neenakosti:

Δx ⋅ ΔP ≥ h

Kjer je h konstanta Plancka. To pomeni, da je negotovost v položaju, pomnožena z negotovostjo v zagonu (masa na hitrost), večja ali enaka plančni konstanti, katere vrednost je zelo majhna, vendar ne nič: H = 6.63 x 10-3. 4 J · s.

In kaj ima načelo negotovosti s tretjim zakonom termodinamike? Če je položaj atomov kristalne mreže fiksiran in natančen (Δx = 0) Potem lahko hitrost teh atomov vzame katero koli vrednost med 0 in neskončnostjo. To je v nasprotju z dejstvom, da v absolutni ničli vsako gibanje toplotne vznemirjenosti preneha.

Vzajemno, če začnemo pri absolutni ničli temperature, vsa vznemirjenost preneha in zagon vsakega atoma omrežja je točno nič (ΔP = 0), potem bi načelo negotovosti Heisenberga pomenilo, da bi bila nedoločnost v položajih vsakega atoma neskončna, to je, da so lahko v katerem koli položaju. 

Zaradi prejšnje izjave bi se število mikrostat ponavadi nanašalo na neskončnost in entropija bi prevzela tudi nedoločeno vrednost. 

Primer 2: Preverjanje in čuden primer helija-4

V odveč, ki se pojavlja pri zelo nizkih temperaturah, zadeva izgubi notranje trenje med svojimi molekulami, imenovano goo. V tem primeru bi lahko tekočina brez trenja krožila za vedno, toda težava je pri teh temperaturah skoraj nič ni tekočina, razen helija.

Helij in helij 4 (njegov najpogostejši izotop) sta edinstven primer, saj pri atmosferskem tlaku in pri temperaturah, ki so blizu absolutne ničle, helij ostane tekoč. 

Ko se helij-4 predloži pri temperaturi pod 2.2 k pri atmosferskem tlaku postane a odveč. To odkritje se je leta 1911 zgodilo v Leydnu z nizozemskim fizikom Heike Kamerlingh Onnes (1853-1926).

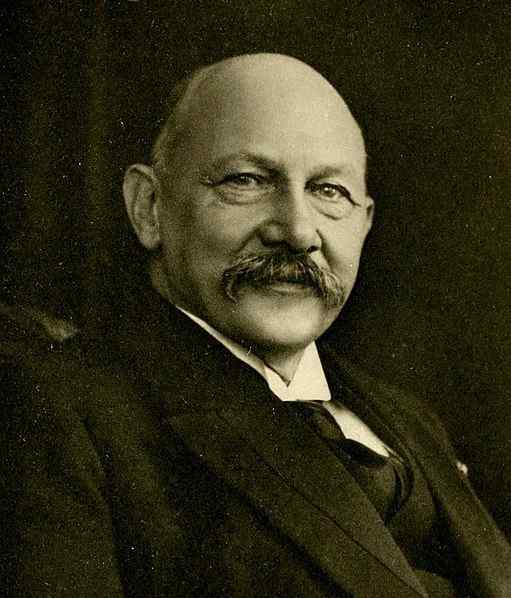Slika 3. Nizozemski fizik Heike Kamerlingh Onnes (1853-1926). Vir: Wikimedia Commons.

Helio-4 atom je a Bosón. Bozoni, za razliko od fermionov, so delci, ki lahko zasedejo vse isto kvantno stanje. Zato Bozoni ne izpolnjujejo Paulijevega načela izključitve.

Nato vsi atomi helija-4 pri temperaturah pod 2.2 K zaseda isto kvantno stanje in zato ni nič drugega kot ena možna mikrostata, kar pomeni, da ima odvečni helij-4 s = 0.

Rešene vaje

- Vaja 1

Razmislite o preprostem primeru, sestavljenem iz sistema, ki ga tvorijo samo trije delci, ki imajo tri ravni energije. Za ta preprost sistem:

a) Določite število možnih mikrostatov za tri temperature:

-visok 

-Polovica 

-Nizka

b) Določite skozi Boltzmannovo entropijo v različnih temperaturnih območjih. 

c) razpravljajte o rezultatih in razložite, ali v nasprotju s tretjim zakonom termodinamike.

Rešitev

Na molekularni in atomski lestvici so energije, ki jih lahko sprejme sistem. Poleg tega, ko so temperature tako nizke, imajo delci, ki sestavljajo sistem. 

Lahko vam služi: magnetna indukcija: formule, kako se izračuna in primeri

Visoka temperatura

Če ima sistem razmeroma visoko temperaturo, imajo delci dovolj energije, da zasedejo vse razpoložljive ravni, kar povzroči 10 možnih mikrostat, ki se pojavijo na naslednji sliki:

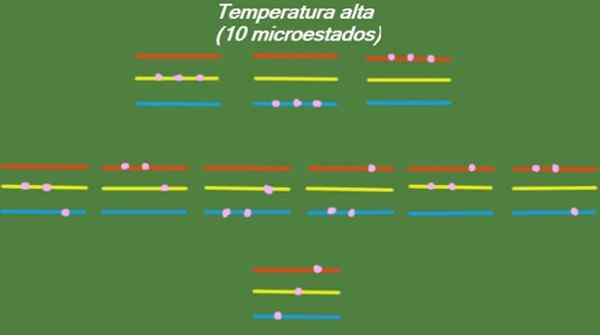Slika 4. Možna stanja pri visoki temperaturi za leto razrešena 1. Vir: Pripravil F. Zapata.

Srednja temperatura

V primeru, da ima sistem vmesno temperaturo, potem delci, ki ga sestavljajo, nimajo dovolj energije, da bi zasedli najvišjo raven energije. Možne mikrostate so prikazane na sliki:

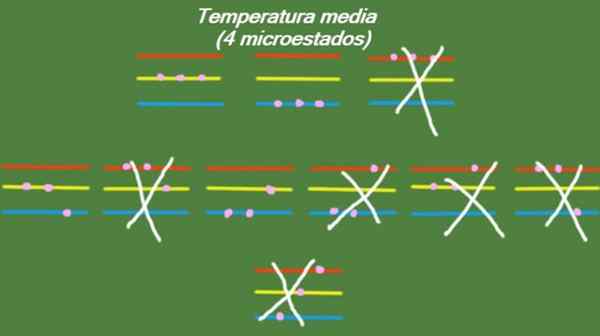Slika 5. Mikro -držav pri povprečni temperaturi za rešeni sistem vadbe 1. Vir: Pripravil F. Zapata.

Nizka temperatura

Če se temperatura še naprej spušča v naše idealizirane tri delce in tri energijske ravni, bodo imeli delci tako malo energije, da bodo lahko zasedli le najnižjo raven. V tem primeru je samo 1 možna mikrostata, kot je razvidno iz slike 6:

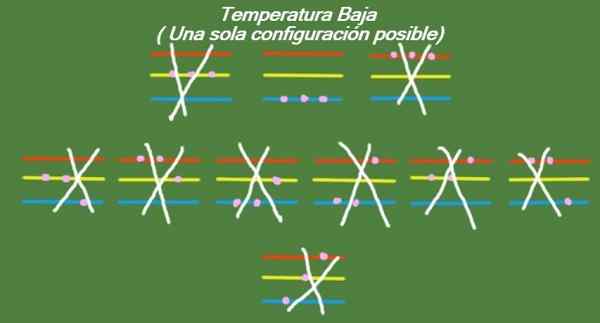Slika 6. Pri nizki temperaturi obstaja možna konfiguracija (lastna izdelava)

Rešitev b

Že znano število mikrostat v vsakem temperaturnem območju, lahko že uporabimo Boltzmannovo enačbo, ki je bila prej dana za iskanje entropije za vsak primer.

S = k ln (10) = 2.30 x k = 3.18 x 10-23 J/k (Visoka temperatura)

S = k ln (4) = 1.38 x k = 1.92 x 10-23 J/k (Srednja temperatura)

In končno:

S = k ln (1) = 0 (Nizka temperatura)

Rešitev c

V prvi vrsti opazimo, da se entropija znižuje, ko se temperatura spušča, kot je bilo pričakovano. Toda za najnižje temperaturne vrednosti je dosežena mejna vrednost, iz katere je doseženo osnovno stanje sistema.

Tudi če je temperatura čim bližje absolutni ničli, ni na voljo manjših stanj. Nato entropija ohranja svojo konstantno minimalno vrednost, kar je v našem primeru s = 0.

Ta vaja ponazarja na ravni mikrostat sistema, razlog, zakaj je tretji zakon termodinamike izpolnjen.

- Vaja 2

Razlog, če je naslednja izjava resnična ali napačna:

"Entropija sistema pri absolutni temperaturi nič je točno nič".

Upravičite odgovor in opišite nekaj primerov.

Rešitev

Odgovor je: FALSE.

Najprej absolutne temperature ni mogoče doseči, ker bi bilo kršeno načelo negotovosti Heisenberga in tretjega zakona termodinamike. 

Zelo pomembno je opaziti, da v tretjem zakonu ni rečeno, kaj se zgodi v absolutnem 0, ko pa je temperatura neskončno blizu Absolute 0. Razlika je subtilna, vendar pomembna.

Tretji zakon ne potrjuje, da ko temperatura po samovoljni vrednosti skorajda blizu Absolute Zero, se entropija nagiba k nič. To bi se zgodilo šele v predhodno analiziranem primeru: Perfect Crystal, ki je idealizacija.

Številni sistemi mikroskopske lestvice, torej v kvantni lestvici, imajo svojo energijsko osnovno raven degenerirano, Kaj pomeni obstoj več konfiguracij na najnižji ravni energije. 

Zgornje pomeni, da v teh sistemih entropija nikoli ne bi bila ravno nič. Niti entropija ne bi bila ravno nič v sistemih, ki so vitrificirani, ko se temperatura nagiba k absolutni ničli. V tem primeru Preostala entropija Prej.

To je zato, ker so bile njihove molekule "zataknjene", preden so zasedle najnižjo stopnjo razpoložljive energije, kar znatno poveča število možnih mikrostatov, zaradi česar je nemogoče entropija točno nič.

Reference

1. Cengel in. 2012. Termodinamika. 7. izdaja. McGraw Hill. 347.
2. Laboratorij za jet pogonski laboratorij. Najbolj kul mesto v vesolju. Okrevano od: ColdAtomlab.Jpl.lonec.Gov.
3. González, a. Entropija in spontanost. Okrevano od: Geocities.Ws
4. Quora. Kaj je praktična uporaba tretjega zakona termodinamike?. Okreval od: Quora.com
5. Splošna kemija. Tretje načelo termodinamike. Okrevano od: Korint.Pucp.Edu.pe
6. Tretji zakon termodinamike. Obnovil od: YouTube.com
7. Wikipedija. Entropija ostanka. Pridobljeno iz: v.Wikipedija.com
8. Wikipedija. Tretji zakon termodinamike. Pridobljeno iz: v.Wikipedija.com