Torricelli teorem

Kaj je Torricellijev teorem?

On Torricelli teorem O Torricelli načelo navaja, da je hitrost tekočine, ki pride skozi luknjo v steni rezervoarja ali posode, enaka, ki jo objekt pridobi prosto spuščeno z višine, ki je enaka hitrosti proste površine tekočine do Luknja.

Teorem je prikazan na naslednji sliki:

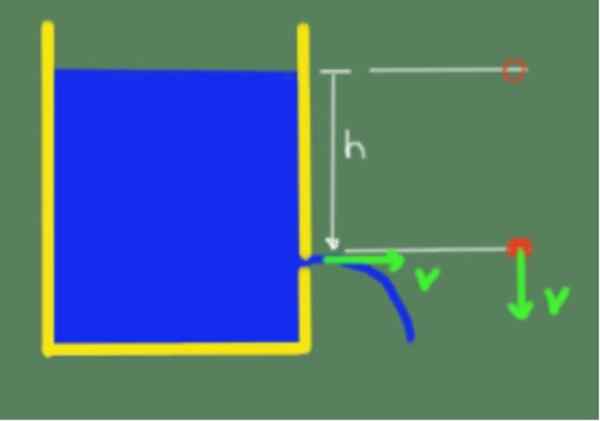Ilustracija Torricellijevega teorema. Vir: Self Made.

Zaradi Torricellijevega teorema lahko nato rečemo, da je hitrost izhoda tekočine z luknjo, ki je do višine h pod prosto površino tekočine, dana z naslednjo formulo:

Kjer je G pospešek gravitacije in je H višina od luknje do proste površine tekočine.

Evangelist Torricelli je bil leta 1608 telesno in matematik, rojen v mestu Faenza v Italiji. Torricelli je pripisan izumu barometra živega srebra in v prepoznavnosti obstaja tlačna enota, imenovana "Torr", enakovredna milimetru živega srebra (mm Hg).

Demonstracija teorema

V Torricellijevem teoremu in v formuli, ki daje hitrost, predvideva, da so izgube zaradi viskoznosti zaničljive, saj se v prostem padcu domneva, da je trenje zaradi zraka, ki obdaja predmet, ki pade, nepomembno.

Prejšnja predpostavka je v večini primerov razumna in pomeni tudi ohranjanje mehanske energije.

Če želite dokazati teorem, bomo na prvem mestu našli formulo hitrosti za predmet, ki se sprosti z ničelno začetno hitrostjo, z enake višine kot površina tekočine v rezervoarju.

Vam lahko služi: trijedimenzionalni valovi: koncept, vrste in primeri

Načelo ohranjanja energije bo uporabljeno za pridobitev hitrosti predmeta, ki pade ravno takrat, ko je višina padla h enako tistemu od luknje do proste površine.

Ker izgube trenja ni, je veljavno uporabiti načelo mehaničnega ohranjanja energije. Recimo, da ima objekt, ki pade, masa m in višina H se meri od ravni izhoda tekočine.

Predmet, ki pade

Ko se objekt sprosti z višine, ki je enaka cesti proste površine tekočine, je njegova energija le gravitacijski potencial, saj je njegova hitrost nič in zato je njegova kinetična energija nič. EP potencialni energijski EP daje:

Ep = m g h

Ko gre pred luknjo, je njegova višina enaka nič, potem je potencialna energija nič, tako da ima samo kinetično energijo EC, ki jo daje:

Ec = ½ m v²

Ker je energija ohranjena, EP = EC tistega, kar je pridobljeno:

½ m v² = M G H

Čiščenje hitrosti v Nato dobimo formulo Torricelli:

Tekočina, ki pride iz luknje

Nato bomo skozi luknjo našli hitrost izhoda tekočine, da bi dokazali, da sovpada s tistim, ki je bil ravno izračunan za predmet, ki prosto pade.

Za to se bomo zanašali na načelo Bernoulli, kar ni nič drugega kot ohranjanje energije, ki se uporablja za tekočine.

Bernoullijevo načelo je oblikovano tako:

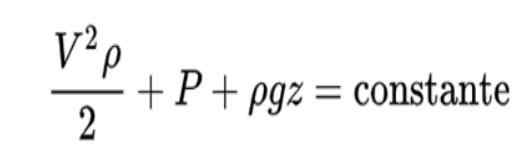
Razlaga te formule je naslednja:

• Prvi izraz predstavlja kinetično energijo tekočine na enoto prostornine
• Drugi predstavlja delo s tlakom na enoto prečnega območja
• Tretji predstavlja gravitacijsko potencialno energijo na enoto volumna tekočine.

Vam lahko služi: trenutna hitrost: definicija, formula, izračun in vaje

Ko začnemo iz premise, ki je idealna tekočina, v ne -turbulentnih pogojih z relativno nizkimi hitrostmi, je pomembno, da potrdimo, da je mehanska energija na enoto v tekočini konstantna v vseh regijah ali prečnih odsekih istega.

V tej formuli V je hitrost tekočine, ρ Gostota tekočine, Str pritisk in z Navpični položaj.

Na spodnji sliki je Torricellijeva formula prikazana na podlagi načela Bernoulli.

Formulo Bernoulli nanesemo na prosti površini tekočine, za katero označujemo (1) in v izhodni luknji, ki jo označujemo (2). Nivo ničelne višine je izbran z izhodno luknjo.

V predpostavki, da je presek v (1) veliko večji kot v (2), lahko nato domnevamo, da je hitrost zmanjšanja tekočine v (1) praktično zanemarljiva.

Zato je V postavljen₁= 0, tlak, na katerega je tekočina podvržena (1), je atmosferski tlak in višina, izmerjena iz luknje, je h.

Za izhodni odsek (2) predpostavljamo, da je izhodna hitrost V, tlak, na katerega je tekočina do iztoka, pa je tudi atmosferski tlak in izhodna višina je enaka nič.

Vrednosti, ki ustrezajo odsekom (1) in (2), se nadomestijo v Bernoullijevi formuli in enaki. Enakost je veljavna, ker predpostavljamo, da je tekočina idealna in ni viskoznih izgub. Ko so vsi izrazi poenostavljeni, se hitrost dobi v izhodni luknji.

Vam lahko služi: rdeči pritlikavec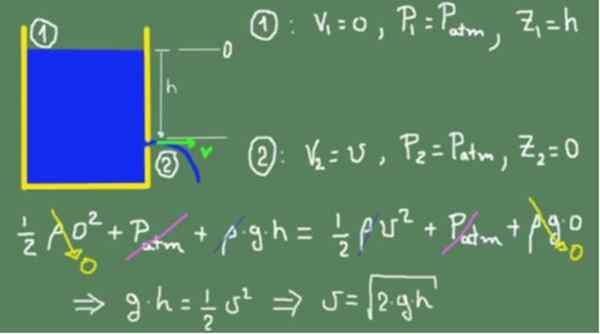

Prejšnje polje kaže, da je pridobljeni rezultat enak rezultatu predmeta, ki prosto pade,

S tem, kar je dokazano, načelo Torricelli.

Rešene vaje

Vaja 1

Yo) Majhna cev za izhodišče rezervoarja za vodo je 3 m pod vodno površino. Izračunajte hitrost iztoka vode.

Rešitev:

Naslednja slika prikazuje, kako se v tem primeru uporablja Torricellijeva formula.

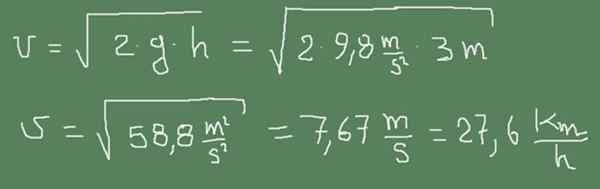
Vaja 2

Ii) Ob predpostavki, da ima izhodna cev prejšnjega rezervoarja za vadbo premer 1 cm, izračunajte tok iztoka vode.

Rešitev:

Pretok je prostornina tekočine, ki izhaja na enoto časa, in se preprosto izračuna tako, da pomnožimo območje izhodne luknje s hitrostjo izhodne hitrosti.

Naslednja slika prikazuje podrobnosti izračuna.

Vaja 3

Iii) Določite, kako višina je prosta površina vode v posodi, če je znana

da v luknji na dnu posoda voda pride do 10 m/s.

Rešitev:

Tudi ko je luknja na dnu vsebnika, je mogoče uporabiti Torricellijevo formulo.

Naslednja slika prikazuje podrobnosti izračunov.

Reference

1. Wikipedija. Torricelli teorem.
2. Hewitt, str. Konceptualna fizikalna znanost. Peta izdaja.119.
3. Mladi, Hugh. 2016. Univerzitetna fizika Sears-Zansky s sodobno fiziko. 14. izd. Pearson. 384.