Kemija

Zgodovina, postulate in primeri molekularne kinetične teorije

Zgodovina, postulate in primeri molekularne kinetične teorije

The Molekularna kinetična teorija To je tisti, ki želi razložiti eksperimentalna opazovanja plinov z mikroskopske perspektive. To pomeni, da poskuša povezati naravo in vedenje plinastih delcev s fizikalnimi lastnostmi plina kot tekočine; Pojasnite makroskopsko iz mikroskopskega.

Plini so bili vedno zanimivi za znanstvenike zaradi svojih lastnosti. Zasedejo celotno količino vsebnika, v kateri so, in se lahko popolnoma stisnejo, ne da bi se vsebina nasprotovala nižji odpornosti; In če se temperatura zvišuje, se posoda začne širiti in lahko celo razpoka.

Plinasti delci v daljnih pogojih ali blizu utekočinjanja. Vir: Olivier Cleynen in uporabnik: Sharayanan [CC BY-SA 3.0 (https: // creativeCommons.Org/licence/by-sa/3.0)]

Mnoge od teh lastnosti in vedenja so povzete v zakonih idealnih plinov. Vendar pa plin štejejo za celoto in ne kot nabor milijonov razpršenih delcev v vesolju; Poleg tega iz podatkov o tlaku, volumnu in temperaturi ne daje več informacij o tem, kako se ti delci premikajo.

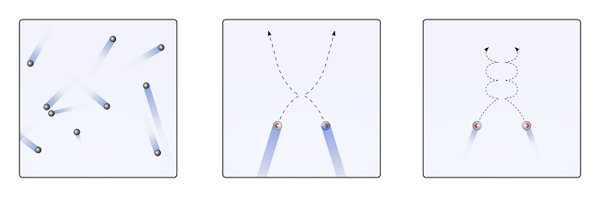
Tako je tako, da molekularna kinetična teorija (TCM) predlaga, da jih vizualizirajo kot mobilne sfere (vrhunska slika). Te sfere se poljubno trčijo med seboj in stene ter vzdržujejo linearno usmeritev. Ko pa se temperatura zniža in se tlak poveča, usmeritev sfer postane krivda.

Plin se mora po TCM obnašati kot sfere prvega polja za sliko. Toda, ko se ohladi in poveča pritisk nanje, se njihovo vedenje oddalji od ideala. Nato so pravi plini, blizu utekočinjenja in gredo v tekočo fazo.

V teh pogojih postanejo interakcije med sferami pomembnejše do te mere, da njihove hitrosti na trenutke počasne. Čim bližje so iz utekočinjanja, več ukriv njihovih usmeritev (desna škatla) postanejo in njihovi trki so manj energije.

[TOC]

Zgodovina

Daniel Bernoulli

Rimski filozof Lucretius je že obravnaval idejo o teh sferah, ki so jih bolje imenovali atomi; Ne za pline, ampak za trdne, statične predmete. Po drugi strani je leta 1738 Daniel Bernoulli uporabil atomski vid na pline in tekočine, tako da si je predstavljal kot neurejene sfere, ki se gibljejo v vseh smereh.

Njegovo delo pa je takrat kršilo zakone fizike; Telo se ni moglo za vedno premakniti, zato je bilo nemogoče misliti, da je niz atomov in molekul trčil drug na drugega brez izgube energije; to pomeni, da obstoj elastičnih trkov ni bil mogoč.

Rudolf Clausius

Stoletje pozneje so drugi avtorji okrepili TCM z modelom, kjer so se plinasti delci premikali v eno smer. Rudolf Clausius pa je sestavil svoje rezultate in oborožil popolnejši model TCM -a, s katerim je želel razložiti idealne zakone o gasu, ki so jih pokazali Boyle, Charles, Dalton in Avogadro.

Vam lahko služi: coulombimetrija: osnove, vrste, aplikacije

James Clerk Maxwell in Ludwig Boltzmann

Leta 1859 je James Clerk Maxwell izjavil, da plinasti delci pri določeni temperaturi kažejo vrsto hitrosti in da jih je mogoče upoštevati s povprečno molekularno hitrostjo.

Nato je leta 1871 Ludwig Boltzmann obstoječe ideje povezal z entropijo in kako termodinamično vedno nagiba k največjemu možnemu prostoru na homogeni in spontani način.

Postulate molekularno kinetično teorijo

Razmisliti o plin iz svojih delcev, model, v katerem so izpolnjene določene postulate ali predpostavke; Postavljeno, da bi moralo biti logično predvideti in razložiti (čim bolj zvesto) makroskopsko in eksperimentalno opazovanje. Glede na to so omenjeni in opisani postulati TCM.

Prostornina plinastih delcev je zanemarljiva

V posodi, polni plinastih delcev, se razpršijo in se odmaknejo med njimi skozi vse vogale. Če bi se lahko za trenutek srečali na določeni točki vsebnika, brez utekočinjanja, bi bilo opaziti, da komaj zasedejo zaničljivi del volumna vsebnika.

Pomeni, da je v posodi, tudi če vsebuje milijone plinastih delcev, res bolj prazen kot polno (razmerje med volumnom in vacío veliko manj kot 1); Torej, če to dopuščajo njegove ovire, lahko on in plin v notranjosti naglo stisnemo; Ker so na računu delci zelo majhni, tako kot njihov volumen.

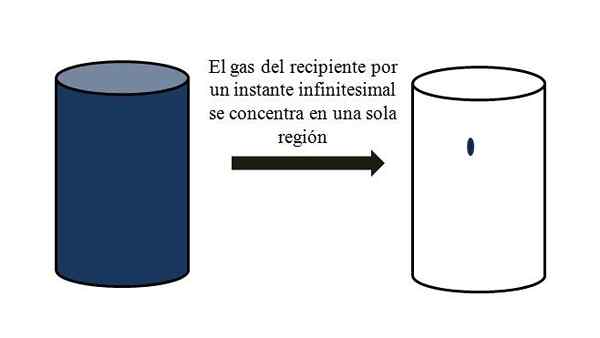Volumen-vacío razmerje plina v posodi. Vir: Gabriel Bolívar.

Vrhunska slika natančno prikazuje, kaj je komentirano zgoraj, z uporabo modrikalnega plina.

Sile privlačnosti med delci so nične

Plinasti delci znotraj vsebnika se med seboj trčijo brez dovolj časa, da njihove interakcije postanejo moč; Še manj, ko je tisto, kar jih v glavnem obkroža, molekularno prazno. Takojšnja posledica tega je, da jim linearne usmeritve omogočajo, da popolnoma pokrijejo prostornino vsebnika.

Če zgoraj navedeno ni bilo tako, bi imela "bizarna" in "labirintna" posoda zaradi mokrih regij zaradi kondenzacije plina; Namesto tega delci potujejo po celotni posodi s polno svobodo, ne da bi jih ustavili njihove interakcije.

Vam lahko služi: klorinska kislina (HClo3) Odpustitev plinastih delcev, kadar so interakcije nične ali nepomembne (do., linearna) in kadar so pomembni (b., krivulje). Vir: Gabriel Bolívar.

Linearne usmeritve zgornje slike (a.) pokazati ta postulat; Če so usmeritve krivulje (b.), dokaz, da obstajajo interakcije, ki jih med delci ni mogoče prezreti.

Plinasti delci so vedno v gibanju

Od prvih dveh postulatov se poleg tega zbližajo, dejstvo, da se delci plinov nikoli ne prenehajo premikati. Ko so v posodi zamegljeni, se trčijo med seboj in s stenami iste, s silo in hitrostjo, ki je neposredno sorazmerna z absolutno temperaturo; Ta sila je, tlak.

Če se plinasti delci nehajo premikati okoli trenutka, bi bili priča znotraj "dimnih jezikov", ki izhajajo iz nič, z dovolj časa, da se naročijo na vakuum in dajo naključne načine.

Trki med delci in stenami posode so elastični

Če elastični trki med plinastimi delci in stenami posode nikoli ne bodo nastali znotraj posode, se nikoli ne bo pojavil (medtem ko se fizični pogoji ne spreminjajo) kondenzacije plina; ali kaj je isto kot reči, da nikoli ne počivajo in se vedno trčijo.

To je zato, ker pri elastičnih trkih ni čiste izgube kinetične energije; Delec trči v steno in odskoči z isto hitrostjo. Če delček, ko trk zmanjša hitrost, drugi pospeši, brez toplote ali zvoka, ki razprši kinetično energijo katerega koli od njih.

Kinetična energija ne ostane konstantna

Gibanje delcev je naključno in kaotično, tako da vsi ne nosijo enake hitrosti; Kot se zgodi, na primer na avtocesti ali v množici. Nekateri so bolj energični in potujejo več hitrosti, drugi pa počasi in čakajo na trk, da jih pospešijo.

Če želite opisati svojo hitrost, je treba izračunati povprečje; In s tem dobimo povprečno kinetično energijo delcev ali plina. Ker se kinetična energija vseh delcev nenehno spreminja, povprečje omogoča boljši nadzor podatkov in lahko delate z večjo zanesljivostjo.

Povprečna kinetična energija je enaka določeni temperaturi za vse pline

Povprečna molekularna kinetična energija (ECMP) V posodi je spremenjen s temperaturo. Pri višji temperaturi bo ta energija večja. Ker je povprečje, lahko obstajajo delci ali soda, ki imajo večjo ali manjšo energijo glede na to vrednost; nekaj hitrejše in počasnejše.

Vam lahko služi: kisline in baze: razlike, značilnosti, primeri

Matematično je mogoče dokazati, da ECMP Odvisno je izključno od temperature. To pomeni, da ni pomembno, kaj plin, njegova molekularna masa ali struktura, njegova ESMP Enako bo pri T -temperaturi in se bo razlikoval le, če se bo povečal ali zmanjšal. Od vseh postulatov je morda to najpomembnejše.

Kaj pa povprečna molekularna hitrost? Za razliko od ECMP, Molekularna masa vpliva na hitrost. Težje je molekula delcev ali plina, naravno je pričakovati, da se bo počasneje premikal.

Primeri

Spodaj je nekaj kratkih primerov, kako je TCM uspelo razlagati zakone idealnih plinov. Čeprav jih ne obravnavajo, je mogoče s TCM razložiti tudi druge pojave, kot sta razširjanje in izliv plinov.

Boyle zakon

Če se prostornina posode stisne pri konstantni temperaturi, se razdalja, ki jo morajo plinasti delci trčiti, da se trči ob stene; ki je enak povečanju pogostosti teh trkov, kar ima za posledico večji pritisk. Ko je temperatura konstantna, ESMP Je tudi konstantna.

Charles Law

Če t, se povečaMP se bo povečala. Plinasti delci se bodo premikali hitreje in večkrat trkali s stenami posode; poveča tlak.

Če so stene prožne in se lahko razširijo, bo njegovo območje postalo večje in pritisk bo padel, dokler ne postane konstanten; In posledično se bo povečala tudi obseg.

Daltonov zakon

Če bi bilo v prostorni posodi dodanih več litrov različnih plinov, iz manjših posod, bi bil njihov skupni notranji tlak enak vsoti delnih tlakov, ki jih ima vsaka vrsta plina posebej.

Ker? Ker se vsi plini začnejo trčiti med seboj in homogeno razpršijo; Interakcije med njimi so praznine, vakuum pa prevladuje v posodi (postulati TCM), tako da je tako, kot da vsak plin najdemo sam, pri čemer je njegov pritisk posamezno brez motenj drugih plinov.

Reference

  1. Whitten, Davis, Peck & Stanley. (2008). Kemija. (8. izd.). Cengage Learning, P 426-431.
  2. Fernández Pablo. (2019). Molekularna kinetična teorija. Vix. Okreval od: vix.com
  3. Jones, Andrew Zimmerman. (7. februar 2019). Kinetična molekularna teorija plinov. Okreval od: Thoughtco.com
  4. Hall Nancy. (5. maj 2015). Kinetična teorija plinov. Glenn Research Center. Pridobljeno iz: GRC.lonec.Gov
  5. Blaber m. & Spodaj s. (9. oktober 2018). Osnove kinetične molekularne teorije. Kemija librettexts. Okrevano od: kem.Librettexts.org
  6. Kinetična molekularna teorija. Pridobljeno od: chemed.Kem.Purdue.Edu
  7. Wikipedija. (2019). Kinetična teorija plinov. Pridobljeno iz: v.Wikipedija.org
  8. Toppr. (s.F.). Kinetična molekularna teorija plinov. Okrevano od: toppr.com