Fizično

Polkrog Kako izračunati obod, območje, centroid, vaje

Polkrog Kako izračunati obod, območje, centroid, vaje

On polkrog Gre za ravno figuro, ki je omejena s premerom oboda in enega od dveh ravnih krožnih lokov, določenih z omenjenim premerom.

Na ta način polkrog meji z a polkrop, ki je sestavljen iz ravnega krožnega loka in ravnega segmenta, ki se pridruži koncem ravnega krožnega loka. Polkrog pokriva polkrog in vse notranjosti kaže na isto.

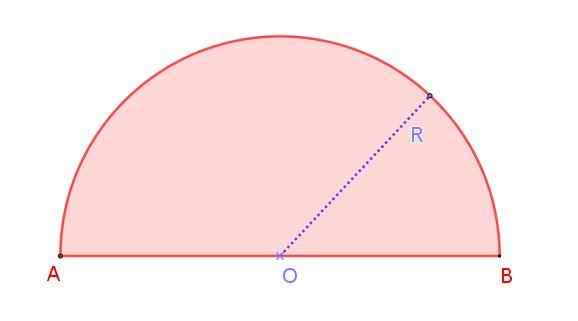Slika 1. Radio r radio polkrop. Vir: f. Zapata.

To lahko vidimo na sliki 1, ki prikazuje radio r rión r, katerega ukrep je polovica premera AB. Upoštevajte, da je za razliko od kroga, v katerem je neskončni premer, v polkrogu le en premer.

Polkrog je geometrijska figura z mnogimi uporabami v arhitekturi in oblikovanju, kot vidimo na naslednji sliki:

Slika 2. Seminicírculo kot dekorativni element v arhitekturi. Vir: Pikist.

[TOC]

Elementi in ukrepi polkroga

Elementi polkroga so:

1.- Ravni krožni lok A⌒B

2.- Segment [AB] 

3.- Notranjost kaže na polkrog, sestavljen iz A⌒B loka in segmenta [AB].

Obod polkroga

Zato je obod vsota konture loka plus v ravnem segmentu:

Perimeter = dolžina loka A⌒B + dolžina segmenta [AB]

V primeru radijskega polkroga r bo njen obod P podan s formulo:

P = π⋅r + 2⋅r = (π + 2) ⋅R

Prvi izraz je polovica oboda oboda polmera r, drugi pa dolžina premera, ki je dvakrat večji polmer.

Vam lahko služi: termometrične lestvice

Območje polkroga

Ker je polkrog eden od ravnih kotnih sektorjev, ki ostane tako, da skozi obseg potegne premer, bo njegovo območje A polovica območja kroga, ki vsebuje radijski polkrog r:

A = (π⋅r2) / 2 = ½ π⋅r2

Centroid polkroga

Centroid polkroga je na svoji osi simetrije do višine, merjene od njegovega premera 4/(3π), krat večji polmer r.

To ustreza približno 0,424⋅r, merjeno iz središča polkroga in na njegovi osi simetrije, kot je prikazano na sliki 3.

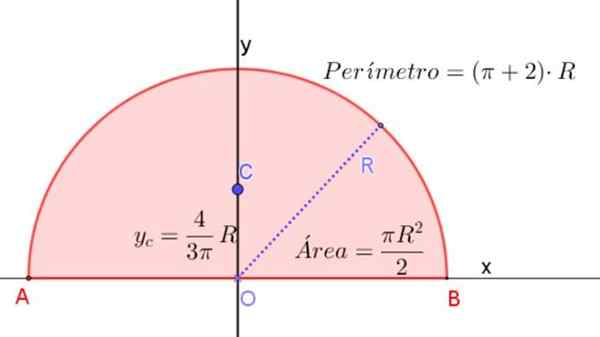Slika 3. Polkrog radia R, ki kaže na formule za določitev območja, oboda in lokacije njenega centra. Vir: f. Zapata.

Inercijski trenutek polkroga

Vzzorevanje inercije ravne figure je opredeljen glede na osi, na primer osi x, kot je:

Integral kvadrata razdalje točk, ki pripadajo figuri na osi. 

Slika 4 prikazuje definicijo trenutka inercije ix polkroga radia R glede na osi x, ki poteka skozi njeno diagonalo:

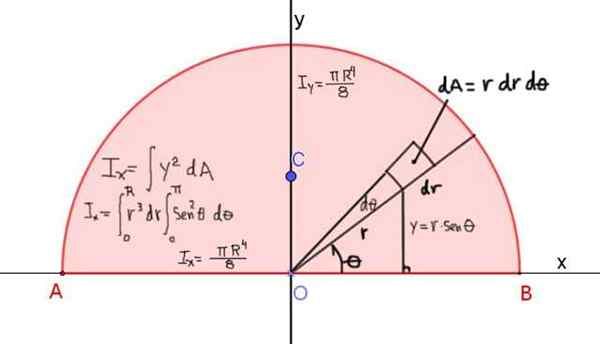Slika 4. Opredelitev inercijskega ix polkroga glede na osi x, ki poteka skozi njeno diagonalo. Rezultat je prikazan za inercijske trenutke glede na osi x in y. Vir: f. Zapata.

Inercijski moment glede na osi X je podan z:

Yox = (π⋅r4) / 8

In inercijski trenutek glede na osi simetrije in je:

Vam lahko služi: valovita optika

Iy = (π⋅r4) / 8

Pokaže, da oba inercijska trenutka sovpadata v njihovi formuli, vendar je pomembno poudariti, da se napotijo ​​na različne osi.

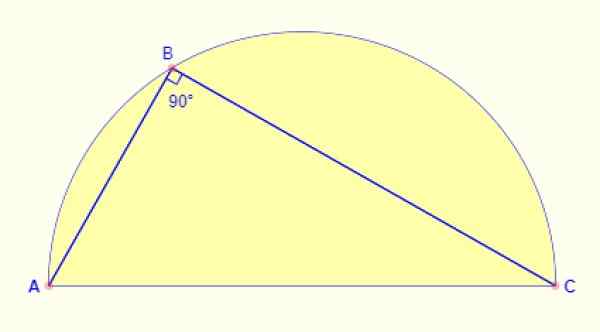
Registrirani kot

Kot, registriran v polkrogu, je vedno 90 °. Ne glede na to, kateri del loka je postavljen do točke, je kot, ki se oblikuje med stranicami AB in BC figure.

Slika 5. Kot, registriran v polkrogu. Vir: Open Reference Math Open.

Rešene vaje

Vaja 1 

Določite obod polmera 10 cm polmera.

Rešitev

Spomnimo se, da je obod, odvisno od polmera, dana s formulo, ki smo jo videli prej:

P = (2 + π) ⋅r

P = (2 + 3,14) ⋅ 10 cm = 5,14 ⋅ 10 cm = 51,4 cm.

Vaja 2

Poiščite območje 10 cm radijskega polkroga.

Rešitev

Formula za območje polkroga je:

A = ½ π⋅r2 = ½ π⋅ (10cm)2 = 50π cm2 = 50 x 3,14 cm2 = 157 cm2.

Vaja 3

Določite višino H centroida polmera polkroga r = 10 cm, izmerjeno iz njegove baze, enako pa je premer polkroga. 

Rešitev

Centroid je polkrožna ravnotežna točka, njegov položaj pa je na osi simetrije na višini h osnove (premer polkroga):

H = (4⋅r) / (3π) = (4⋅10 cm) / (3 x 3,14) = 4,246 cm

Vaja 4

Poiščite inercijski moment polkroga glede na osi, ki sovpada z njegovim premerom, vedoč, da je polkrog izdelan iz tankega lista. Njegov polmer je 10 cm, njegova masa pa 100 gramov.

Rešitev

Formula, ki daje inercijski trenutek polkroga, je:

Vam lahko služi: fizika trdnega stanja: lastnosti, struktura, primeri

Yox = (π⋅r4) / 8

Ker pa nam težava pove, da gre za materialni polkrog, je treba predhodno razmerje pomnožiti s površinsko gostoto polkrožne mase, ki jo bo označil σ.

Yox = σ (π⋅r4) / 8

Nato določimo σ, kar ni nič drugega kot masa polkroga, razdeljeno med površino istega.

Območje je bilo določeno v vaji 2 in rezultat je bil 157 cm2. Potem bo površinska gostota tega polkroga:

σ = 100 gramov / 157 cm2 = 0,637 g/cm2

Nato se inercijski trenutek glede na premer izračuna na naslednji način:

Yox = (0,637 g/cm2) [3,1416 ⋅ (10 cm)4]/ 8

Rezultat:

Yox = 2502 g⋅cm2

Vaja 5

Določite moment vztrajnosti polmera polkroga 10 cm, zgrajenega iz materialnega lista s površinsko gostoto 0,637 g/cm2 z osi, ki poteka skozi njegovo sredino in je vzporedna s premerom.

Rešitev

Za rešitev te vaje se je treba spomniti Steinerjevega izrekanja o trenutkih vztrajnosti vzporednih osi, ki pravi:

Moment inercije I glede na osi, ki je na razdalji H centroida, je enak vsoti inercije Ic Kar zadeva osi, ki poteka skozi centroid in je vzporedna s prvim produktom testa skozi kvadrat ločitve obeh osi.

I = ic + M h2

V našem primeru je znano, da gre za vztrajnost glede na premer, ki je bil že izračunan v vaji 4. H pozna tudi med premerom in centroidom, ki je bil izračunan v vaji 3.

Očistiti moramo IC:

Yoc = I - m h2

Yoc = 2502 g⋅cm2 - 100G ⋅ (4.246 cm)2 Rezultat vztrajnosti z osi vzporedno s premerom, ki gre skozi sredino, je: 

Yoc = 699,15 g⋅cm2

Reference

  1. Aleksander, d. 2013. Geometrija. 5. Izdaja. Cengage učenje.
  2. Open Reference Math Open. Polkrog. Okreval od: Mathpenref.com.
  3. Formule vesolja.Polkrog. Okrevano od: univerzeformulas.com.
  4. Formule vesolja. Območje polkroga. Okrevano od: univerzeformulas.com.
  5. Wikipedija. Polkrog. Pridobljeno iz: v.Wikipedija.com.