Vektorski grafični podstavki

The Odštevanje vektorja o Vektorska odštevanje med vektorji ali in v označeno s ali - v, Izračuna se z dodajanjem vektorja ali z nasprotnim vektorjem v. Algebraično je odštevanje izraženo na naslednji način:

ali - v = ali + (-v)

Odštevanje vektorjev je mogoče izvesti po različnih postopkih, na primer v grafični obliki, na ta način vektor v Nariše ga orientirani linijski segment -puščica-.

Dolžina puščice ustreza vektorskemu modulu, naklon - glede na določeno referenčno črto - označuje smer in konec označuje smer vektorja.

Vektor, ki nasprotuje v Ima enako dolžino in smer, vendar drugače. Nato, pred odštevanjem ali in v, Potrebno je narisati nasprotni vektor v, in dodajte ta vektor v u.

Zelo pomembno je poudariti, da odštevanje vektorjev ni komutativno, to je, da vrstni red vektorjev spremeni rezultat, torej:

ali - v ≠ v - ali

Grafični postopek je mogoče izvesti z uporabo katere koli od teh metod, katere korake bomo razložili spodaj:

-Metoda trikotnika.

-Metoda paralelograma.

[TOC]

Grafična vektorska sub -grafična metoda

Metoda trikotnika

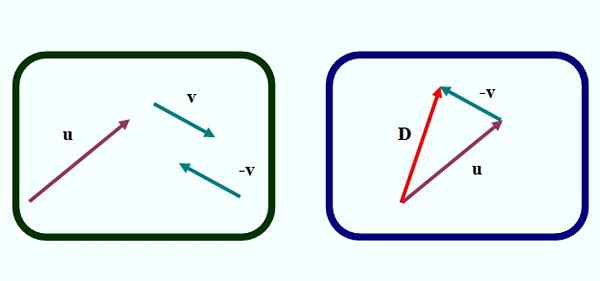
Slika 1. Vektorji se podpirajo po metodi trikotnika. Vir: f. Zapata.

Na sliki 1 imamo prvo od metod za grafično odštevanje dveh vektorjev. To je približno Metoda trikotnika, Ker je figura, ki nastane pri vzpostavljanju vektorjev, trikotnik, kot lahko vidimo na levi sliki.

Odšteti ali - v Nadaljujemo na naslednji način:

-Narišite vektor -v Iz vektorja v, s prevodom s pravilom in ekipo, vendar spreminjanje smeri puščice (leva slika).

-Se preseli v vektor -v na tak način, da njen izvor sovpada s koncem vektorja ali (desna slika).

Vam lahko služi: Trenje: vrste, koeficient, izračun, vaje

-Nato se nariše vektor (rdeče na pravi sliki), ki sega od izvora ali do konca v. KLIČITE D In to je vektorska razlika:

D = ali - v

Metoda paralelograma

Pri metodi paralelograma morajo vektorji, ki jih je treba dodati ali odštevati. Recimo, da želimo najti ali - v Z zgornjimi vektorji so koraki za iskanje odštevanja vektorjev po tej metodi naslednji:

-Določite nasprotni vektor v, kaj je -v, kot je opisano že za metodo trikotnika.

-Previdno vzemite vektorje ali in -v na tak način, da njen izvor sovpada.

-Zdaj segmentirane vzporedne črte narišejo s koncev vsakega vektorja. Slika, ki je nastala, je paralelogram in v posebnih primerih, v katerih so vektorji pravokotni, je pravokotnik ali kvadrat.

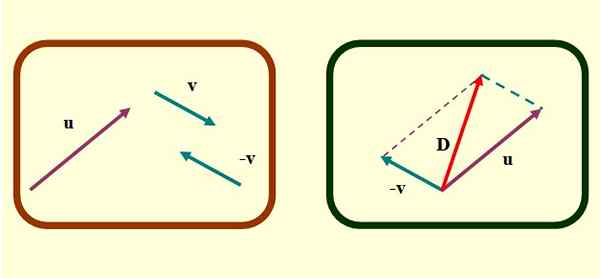Slika 2. Metoda paralelograma za odštevanje vektorjev. Vir: f. Zapata.

-Končno vektor, ki sega iz skupnega izvora ali in v do konca, kjer so prekrižane segmentirane vzporedne črte. To je vektor D ali odštevanje.

Pomembno

Drug način za odštevanje je narisati paralelogram, kot da želite dodati vektorje.

Toda namesto da bi risali običajno diagonalo vsote, ki sega od skupnega izvora do presečišča vzporednic, Diagonalno nasprotje ali krajše, Kot je razvidno iz slike:

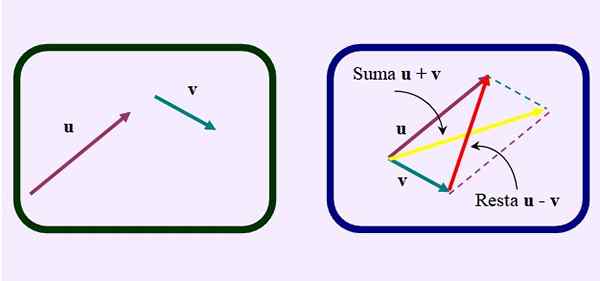Slika 3. Drug način za izvajanje vektorskega odštevanja z metodo paralelograma. Vir: f. Zapata.

Primeri odštevanja vektorja

- Primer 1

Ladja krmi v reki in to počne v nasprotni smeri toka. Opazovalec na zemljišču opaža, da se hitrost ladje zmanjša zaradi delovanja toka.

Vam lahko služi: kaj pa energija, ki jo vsebuje materiala?

Hitrost je vektor in v tem primeru hitrost ladje kaže v eno smer, tok pa ima isto smer in nasprotno smer. Neto hitrost ladje je vsota obeh vektorjev.

Na primer, če instrumenti plovila. Kot v = v ' +vc, saj je vc hitrost toka, ki se izračuna s odštevanjem hitrosti V in V': vc = v - v '= 30 km/h - 40 km/h = -10 km/ h.

- Primer 2

V kinematografiji imamo pomembne vektorje, ki opisujejo spremembe:

-Premik za spremembe položaja.

-Povprečna hitrost, da količinsko določi, kako hitro se položaj spreminja v času.

-Pospešek za spreminjanje hitrosti kot funkcija časa.

Vektor premika

Vektor premika opisuje spremembo položaja, ki ga telo doživlja med svojim gibanjem.

Oglejmo si na primer delček, ki opisuje ravno usmeritev, prikazano na sliki, v kateri gre od točke P₁ do točke p₂.

Vektorji, usmerjeni od izvora koordinatnega sistema X-Y, na te točke so položaj r₁ in r₂, Medtem ko je vektor premika δr, sega od str₁ A p₂. Res je, da:

Δr = r₂ - r₁

Zato je vektor premika odštevanje med končnim položajem in začetnim vektorjem, kot je navedeno na naslednji sliki. Njegove enote so tudi tiste v položaju: metri, stopala, milje, centimetri in še več.

Vam lahko služi: Perseus (ozvezdje): lokacija, mitologija in značilnosti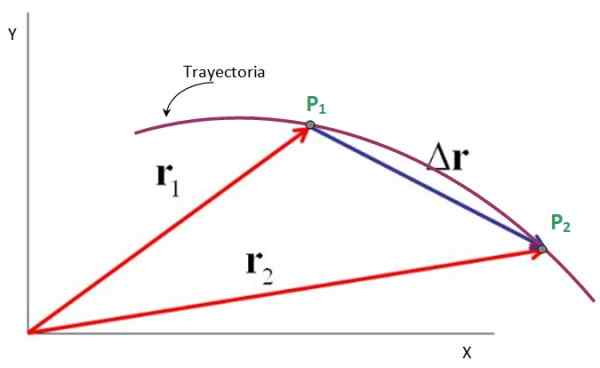Slika 4. Vektor za premik je razlika med končnim in začetnim položajem. Vir: f. Zapata.

Povprečni vektorji hitrosti in povprečnih pospeškov

Vektor povprečne hitrosti v_m Opredeljen je kot premik, pomnožen z obratnim časovnim intervalom:

 In povprečni pospešek je:

Vaja rešena

Delček, ki opisuje krog, traja 5 s, da preide od točke A do točke B. V A ima hitrost v_Do = 60 km/h proti osi +x in b je v_B = 60 km/h proti +in. Določite njegov povprečni pospešek v grafični in analitični obliki.

Rešitev

V grafični smeri in pomenu povprečnega pospeška določa::

Na naslednji sliki je odštevanje v_B - v_Do, prek metode trikotnika od povprečnega pospeška do_m je sorazmerno z δv. Trikotnik ima dve kategoriji enaki in zato akutni notranji koti merijo 45 °.

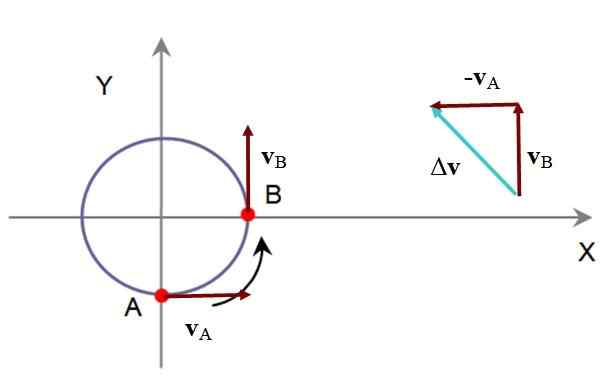Slika 5. Diagram gibanja delcev rešenega primera. Vir: f. Zapata.

Analitično, če naslov +x sovpada z vektorjem enote Yo in +naslov in z vektorjem enote J, tako:

Δv = 60 km/h J - 60 km/h Yo

Jemanje Δt = 5 s, po podatkih izjave je povprečni pospešek:

do_m = (60 km/h J - 60 km/h Yo) / 5 s = 12 (J-Yo) Km/(h.s)

Reference

1. Bauer, w. 2011. Fizika za inženiring in znanosti. Zvezek 1. MC Graw Hill.
2. Bedford, 2000. Do. Mehanika za inženiring: statična. Addison Wesley.
3. Figueroa, d. (2005). Serija: Fizika za znanost in inženiring. Zvezek 1. Kinematika. Uredil Douglas Figueroa (USB).
4. Giambattista, a. 2010. Fizika. 2. mesto. Ed. McGraw Hill.
5. Sears, Zemansky. 2016. Univerzitetna fizika s sodobno fiziko. 14. Ed. Zvezek 1.
6. Tipler, str. 2006. Fizika za znanost in tehnologijo. 5. izd. Zvezek 1. Uredništvo se je vrtelo.