Sarrus pravilo

Sarrus pravilo. Vir: Uporabnik: Sevela.P, cc by-sa 4.0, Wikimedia Commons

Kaj je Sarrusovo pravilo?

The Sarrus pravilo To je tehnika za izračun dejavnikov kvadratne matrice 3 × 3 ali več. Ta sistem omogoča lažje rešitve. Uporablja se tudi za določitev, ali so vektorski kompleti linearno neodvisni in tvorijo osnovo vektorskega prostora.

Te aplikacije temeljijo na obribilnosti matric. Če je matrica redna, je njegova determinanta drugačna od 0. Če je edinstvena, je njena odločilna vredna 0. Determinante je mogoče izračunati le v kvadratnih matricah.

Za izračun matric katerega koli reda lahko uporabite teorem Laplacea. Ta teorem nam omogoča poenostavitev matric visokih dimenzij v vsotah majhnih determinantov, ki jih razgradimo z glavne matrice.

Navaja, da je determinanta matrice enaka vsoti produktov vsake vrstice ali stolpca, z determinantom pritrjene matrice.

To zmanjšuje determinante, tako da determinant stopnje N postane determinant N-1. Če to pravilo uporabimo zaporedno, lahko pridobimo determinante dimenzije 2 (2 × 2) ali 3 (3 × 3), kjer je njegov izračun veliko lažji.

Sarrus pravilo

Pierre Frederic Sarrus (1798-1861) je bil francoski matematik. Večina njegovih matematičnih pogodb temelji na metodah ločljivosti enačb in izračunu variacij v numeričnih enačbah.

V eni od svojih pogodb je rešil enega najbolj zapletenih enigme mehanike. Za reševanje težav z artikuliranimi komadi je Sarrus uvedel preoblikovanje alternativnih pravokotnih gibov v enakomernih krožnih gibih. Ta novi sistem je znan kot Sarrus mehanizem.

Lahko vam služi: eksternalizacija in internalizacija stroškov

Raziskava, ki mu je najbolj dala, je bila tista, v kateri je predstavil novo metodo izračunavanja dejavnikov, v članku "Nouvelles Metodas Pour la Résolution des équations" ("Nova metoda za ločljivost enačb"), objavljena leta 1833. Ta način reševanja linearnih enačb je znan kot Sarrusovo pravilo.

Pravilo Sarrus omogoča izračun determinanta matrice 3 × 3, ne da bi uporabil Laplasov teorem, uvaja veliko preprostejšo in bolj intuitivno metodo. 

Da bi lahko preverili vrednost pravila Sarrus, vzamemo katero koli matrico dimenzije 3:

Izračun njene determinante bi bil izdelan iz njegovih glavnih diagonalov, ki bi izdelek odšteval od inverznih diagonalov. To bi bilo naslednje:

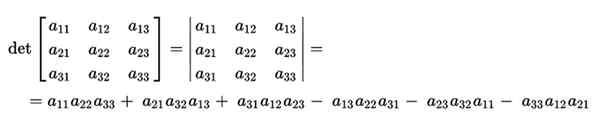
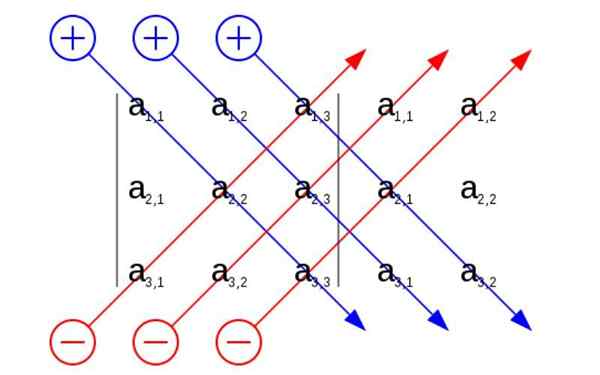
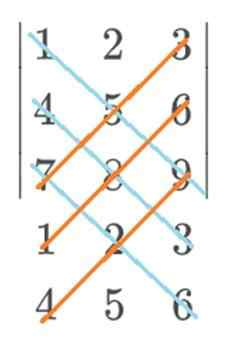
Pravilo Sarrusa nam omogoča, da pri izračunu diagonalov določitve pridobimo veliko enostavnejši vid. Poenostavljeno bi bilo, če bi na zadnji del matrice dodali prva dva stolpca.

Na ta način je bolj jasno glede njegovih glavnih diagonalov in na obrazu za izračun izdelka.

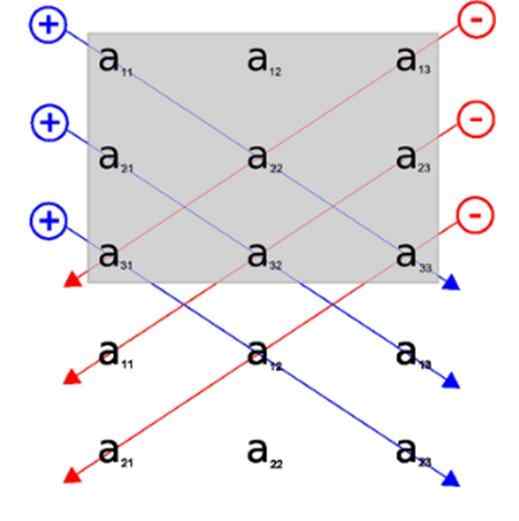
Skozi to sliko si lahko ogledamo uporabo pravila Sarrus, v vrstico 1 in 2 vključujemo pod grafično predstavitev začetne matrice. Na ta način so glavne diagonale tri diagonale, ki se pojavijo na prvem mestu.

Tri obratne diagonale so tiste, ki se najprej pojavijo zadaj.

Na ta način se diagonale pojavijo na bolj vizualni način, ne da bi zapletli ločljivost determinanta, poskušali ugotoviti, kateri elementi matrice pripadajo vsaki diagonali.

Vam lahko služi: quechua besede, prevedene v španščino

Kot je razvidno iz slike, izberemo diagonale in izračunamo izdelek, ki je iz vsake funkcije. Diagonale, ki se pojavljajo v modri barvi, so tiste, ki seštevajo. Vsoto teh odštejemo vrednost diagonalov, ki se pojavljajo v rdeči barvi.

Da bi bilo stiskanje lažje, lahko uporabimo numerični primer, namesto da uporabimo algebrske in podtezne izraze.

Če vzamemo katero koli matrico 3 × 3, na primer:

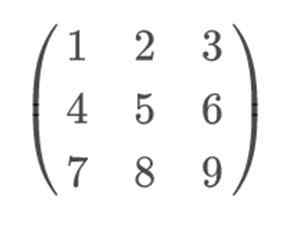
Če želite uporabiti pravilo Sarrusa in ga rešiti na bolj vizualni način, bi morali vključiti vrstico 1 in 2, kot vrstico 4 oziroma 5. Pomembno je vzdrževati vrstico 1 v 4. položaju in 2. vrstico v 5. Ker če jih izmenjamo, pravilo Sarrusa ne bo učinkovito.

Za izračun odločilnika bi bila naša matrica naslednja:

Za nadaljevanje z izračunom bomo pomnožili elemente glavnih diagonalov. Spuščanje, da se začnejo na levi.

V tem primeru bi modra šla s pozitivnim znakom in rdečo z negativnim znakom. Končni izračun pravila Sarrusa bi ostal tako:

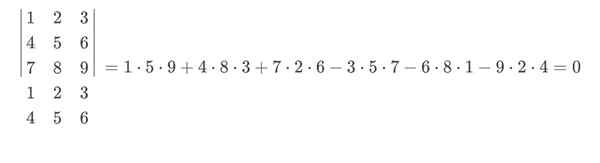
Fantje dejavnikov

Determinant dimenzije 1

Če je matrična dimenzija 1, je matrica na ta način: a = (a)

Zato bi bila njena determinanta naslednja: det (a) = | a | = a

Povzeto je determinanta matrice A enaka absolutni vrednosti matrice A, ki je v tem primeru a.

Deternictinant Dimension 2

Če gremo na matrike dimenzije 2, dobimo matrike tipa:

Vam lahko služi: taumaticgy

Kjer je njena determinanta opredeljena kot:

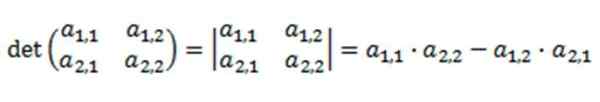
Resolucija tega determinanta temelji na množenju njegove glavne diagonale, ki odšteje produkt njegove obratne diagonale.

Determinant dimenzije 3

Če je matrična dimenzija 3, bi bila nastala matrica te vrste:

Determinant te matrice bi se na ta način rešili s pravilom Sarrusa:

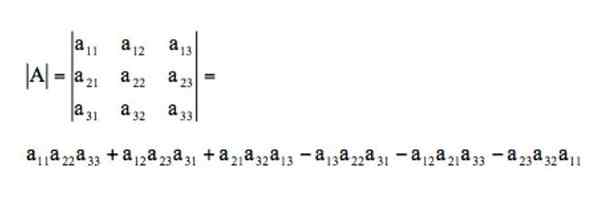
Reference

1. Anthony Nicolaides (1994). Determinant & Matrics. Pass publikacija.
2. M. Casteleiro Villalba (2004). Uvod v linearno algebro. ESIC uvodnik.