Kaj je kapacitivna reaktanca in kako jo izračunati?

The kapacitivna reaktanca Upor je, da kondenzator, regulativni element toka obremenitve v vezju izmeničnega toka, nasprotuje prehodu toka.

V vezju, sestavljenem iz kondenzatorja in aktivira z izmeničnim tokom, lahko definiramo kapacitivno reaktanco x_C kot sledi:

X_C = 1 / ωc

Slika 1. Kapacitivne reakcije so del Passabajos filtrov in govorcev govorcev. Vir: Pixabay.

Ali tudi:

X_C = 1 / 2πfc

Kadar je C zmogljivost kondenzatorja in ω, je kotna frekvenca vira, povezana s frekvenco F do:

Ω = 2πf

Kapacitivna reaktanca je odvisna od inverzne frekvence, zato je pri visokih frekvencah majhna, pri nizkih frekvencah.

Mednarodna sistemska enota za merjenje kapacitivne reaktance je OHM (ω), pod pogojem, da je zmogljivost kondenzatorja v Faradu, (skrajšana F) in frekvenca je izražena v obratu sekund^-1).

Medtem ko obremenitev traja, se skozi kondenzator vzpostavi tudi napetost in tok, katerih največje amplitude ali vrednosti so označene kot V_C in jaz_C, Povezani so s kapacitivno reaktanco, ki je analogna OHM -ovemu zakonu:

V_C = I_C ⋅ x_C

V kondenzatorju se napetost zavleče 90 ° glede na tok ali pa je napredna 90 ° glede na to, kot je prednostno. Vsekakor je frekvenca enaka.

Ko x_C Je zelo velik, tok je majhen in daje vrednost x neskončno_C, Kondenzator se obnaša kot odprto vezje in tok je nič.

[TOC]

Kako izračunati kapacitivno reaktanco

Poglejmo primer, kako izračunati kapacitivno reaktanco: predpostavimo, da je kondenzator 6 μF povezan z izmeničnim iztokom in frekvenco in frekvenco F 60 Hz.

Za iskanje kapacitivne reaktance se uporablja definicija na začetku. Kotna frekvenca ω je podana z:

Lahko vam služi: magnetna indukcija: formule, kako se izračuna in primeri

Ω = 2πf = 2π x 60 Hz = 377 s^-1

Potem se ta rezultat nadomesti v definiciji:

X_C = 1 / ωc = 1 / (377 s^-1x 6 x10 ^-6 F) = 442.1 ohm

Zdaj pa poglejmo amplitudo toka, ki kroži v vezju. Ker vir ponuja amplitudno napetost V_C = 40 V, za izračun amplitude največjega toka ali toka uporabimo razmerje med kapacitivno reaktanco, tokom in napetostjo:

Yo_C = V_C / X_C = 40 V / 442.1 ohm = 0.09047 a = 90.5 m a.

Če frekvenca postane zelo velika, kapacitivna reaktanca postane majhna, če pa je frekvenca postala 0 in smo imeli neposreden tok, bi bila reaktanca ponavadi neskončna.

Napetost toka in kondenzatorja

Ko se kondenzator poveže z virom izmeničnega toka, kot je, da niha in spremeni svojo polarnost, kondenzator izmenično doživi obremenitve in izpuste.

Za frekvenco 60 Hz, kot je primer, je napetost pozitivna 60 -krat na sekundo in negativna še 60 -krat na sekundo.

Slika 2. Preprosto vezje kondenzatorja in vir izmeničnega toka. Vir: f. Zapata.

S povečanjem napetosti poganja tok v eno smer, če pa se kondenzator nalaga, se tok pojavi v nasprotni smeri, ki nasprotuje prvi.

DA V_C (t) = v_m Sen ωt, če vemo, da je zmogljivost razlog med obremenitvijo in napetostjo, bomo imeli obremenitev:

C = Q/V → Q (T) = CV = CV_m Sen ωt

In če imamo obremenitev odvisno od časa, bomo imeli tok, ki je izpeljan iz tega:

Yo_C(t) = cv_m Ω cos ωt

Toda dojke in kosinus sta povezana s: cos α = sin (α + π/2), torej:

Yo_C(t) = cv_m Ω sena (ωt + π/2) = i_C Sen (ωt + π/2)

Z i_C = Cv_C Ω

Kot je razvidno, je razlika 90 ° predplačilo toka glede na napetost, kot je komentiral na začetku.

Vam lahko služi: Millikan Experiment: postopek, razlaga, pomen

V opisu te vrste vezij, koncept Fasor, ki je zelo podobna vektorju in omogoča, da v kompleksni ravni predstavlja kakršno koli izmenično količino, kot so tok, napetost ali impedanca.

Naslednja slika prikazuje na desni strani napetosti in toka v kondenzatorju, ki tvorijo kot 90 °, kar je zaostajanje med obema.

Na levi so ustrezni grafi, različnih amplitud, vendar enaka frekvenca. Sčasoma tok napreduje proti napetosti in ko je ta največji, je tok nič in ko je napetost enaka, je tok največji, vendar z obrnjeno polarnostjo.

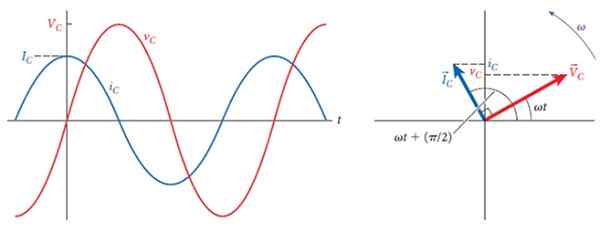Slika 3. 90 ° zaostajanje med tokom in napetostjo skozi kondenzator. Vir: Bauer, W.

Kompleksna impedanca kondenzatorja

V vezju z upori, kondenzatorji in induktivnosti je reaktanca namišljen del z impedance, zapletena količina, ki ima v vezjih izmeničnega toka vlogo, podobno kot pri električnem uporu za neposredni tok, ki je neposredni tok.

Pravzaprav je impedanca vezja opredeljena kot razlog med napetostjo in tokom:

Z = v / i

Za kondenzator ali kondenzator je njegova impedanca podana s količnikom:

Z_C = v (t) / i (t) = v_C Sen ωt / i_C Sen (ωt + π/2)

Način izražanja napetosti in toka kot fasores je označiti amplitudo in fazni kot (polarna oblika):

v (t) = v_C ∠ 0 °

I (t) = i_C ∠ 90 °

Zato:

Z_C = V_C ∠ 0 ° / i_C ∠ 90 ° = (V_C / Yo_C) ∠ 0 ° -90 ° =

= V_C / Cv_C Ω ∠ -90º = (1/ ωc) ∠ -90 ° =

Z_C = (- j) x_C

To pomeni, da je impedanca kondenzatorja njegova kapacitivna reaktanca, pomnožena z negativnim namišljenim enotom.

Impedanca serijskega RC vezja

Impedanca izmeničnega toka z uporom, kondenzatorji in induktorji lahko predstavljamo tudi binomno z:

Lahko vam služi: prvi zakon termodinamike: formule, enačbe, primeri

Z = r + jx

V tej enačbi R predstavlja upor, ki ustreza resničnemu delu, j je namišljena enota, x.

Če vezje vsebuje upor in serijski kondenzator, je njegova impedanca:

Z = z_R + Z_C    

Kot v uporni napetosti in toku sta v fazi, je uporovna impedanca preprosto vrednost upora r.

V primeru kapacitivne impedance smo že videli, da je z_C = -Jx_C , Zato je impedanca RC vezja:

Z = r - jx_C = R - j (1/ ωc)

Na primer v spodnjem vezju, katerega vir je v obliki:

100 V ⋅ sena (120πt)

Opažamo, da je ω = 120π, impedanca je:

Z = 83.0 - J [(1 / (120π ⋅ 6 x 10^-6)] ohm = 83.0 - 442.1 j ohm.

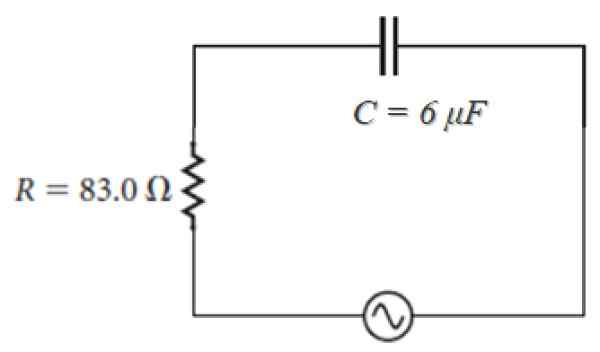Slika 4. RC vezje z izmeničnim tokom. Vir: f. Zapata.

Kapacitivne reakcijske aplikacije

Visoki filtri PASA, filtri z nizkim prehodom, mostna vezja za merjenje kapacitivnosti in induktivnosti ter vezja hladilnika so med glavnimi aplikacijami, ki vsebujejo kapacitivne reakcije v kombinaciji z induktivnostmi in električno upornostjo.

V zvočni opremi nekateri zvočniki prihajajo z ločenimi vrstami vrste Woofer (večji) za nizke frekvence in Tviter ali majhen rog za visoke frekvence. Na ta način se izboljšata zmogljivost in kakovost zvoka.

Uporabljajo se kondenzatorji, ki preprečujejo prihod nizkih frekvenc v tviter, medtem ko v nizkotonec doda induktor, da se izognemo visokim frekvenčnim signalom, saj ima induktivnost reaktant, sorazmerna s frekvenco: x x_L = 2πfl.

Reference

1. Aleksander, c. 2006. Temelji električnega vezja. 3. mesto. Izdaja. MC Graw Hill.
2. Bauer, w. 2011. Fizika za inženiring in znanosti. Zvezek 2. MC Graw Hill.
3. Figueroa, d. 2005. Serija: Fizika za znanost in inženiring. Zvezek 6. Elektromagnetizem. Uredil Douglas Figueroa (USB).
4. Giancoli, d.  2006. Fizika: načela z aplikacijami. 6. Ed Prentice Hall.
5. Serway, r., Jewett, J. 2008. Fizika za znanost in inženiring. Zvezek 1. 7. Ed. Cengage učenje.