Kakšen je magnetni trenutek?

On Magnetni trenutek To je vektor, ki navaja tok, ki prečka nekoliko ali zaprto zanko z območjem istega. Njegov modul je enak produktu intenzivnosti toka po območju, njena smer in smer pa daje pravilo desne roke, kot je prikazano na sliki 1.

Ta definicija je veljavna ne glede na to. Kar zadeva enotnost magnetnega trenutka, v mednarodnem sistemu enot, če je ampere × m².

Slika 1. Vektor magnetnega trenutka poljubne vezi je pravokoten na njeno ravnino, smer pa določa pravilo desnega palca. Vir: Wikimedia Commons.

V matematičnem smislu označuje vektorski magnetni trenutek z grškim besedilom μ (Krepko, ker je vektor in se tako loči od njegove velikosti), se izraža kot:

μ = Ia n

Kjer sem intenzivnost toka, je A območje, ki obdaja zanko in n To je enota vektor (modula, ki je enak 1), ki kaže v smeri, pravokotno na ravnino lopatice in katerih pomen daje pravilo desnega palca (glej sliko 1).

To pravilo je zelo preprosto: zavijanje štirih prstov desne roke, tako da sledijo toku, palec označuje smer in smer n in torej magnetni trenutek.

Prejšnja enačba velja za zanko. Če obstajajo nougas kot v tuljavi, se magnetni trenutek pomnoži z n:

μ = nIa n

[TOC]

Magnetni trenutek in magnetno polje

Za magnetni trenutek obratov je enostavno najti izraze z običajnimi geometrijskimi oblikami:

-Kvadratna stran strani ℓ: μ = Iℓ² n

-Strani pravokotne spirale do in b: μ = IAB n

-Radio R. Radio Spira: μ = Iπr² n

Vam lahko služi: atomska številka

Dipolovo magnetno polje

Magnetno polje, ki ga proizvaja trenutna zanka ali spaza.

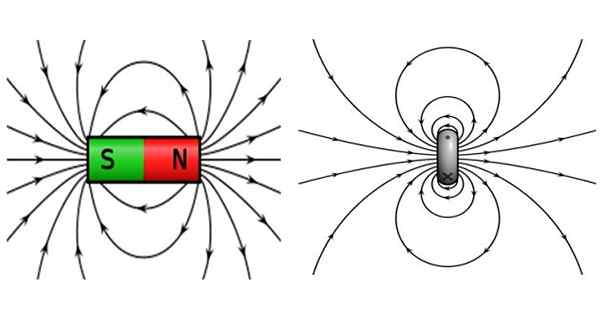Slika 2. Na levi strani magnetnega polja paličnega magneta in na desni, ki proizvaja krožno spiralo, ki prevaža tok. Vir: Wikimedia Commons.

Za magnete so značilni, da imata severno in južni pol, kjer se privlačijo nasprotni polu in isti polji odbijajo. Terenske črte so zaprte, zapustite severni pol in dosežete Južni pol.

Zdaj so magnetni drogovi nerazdružljivi, kar pomeni, da če je magnet, če je magnet razdeljen na dva manjša magneta, še naprej imajo svoj severni in južni polov. Izoliranih magnetnih polov ni mogoče imeti, zato se imenuje magnet Magnetni dipolo.

Magnetno polje polmera r spirale r, ki prevaža tok I, izračuna zakon o Biot-Savart. Za točke, ki pripadajo svoji osi simetrije (v tem primeru osi x), je polje podano z:

Kjer μ_tudi Je prepustnost vakuuma. Polje, ki se oddaljuje od točk stran od lopata, za kar je izpolnjeno, da se X >> r približa:

Razmerje med magnetnim poljem in magnetnim mostom dipola

Vključno z magnetnim trenutkom v prejšnjem izrazu je:

Na ta način je intenzivnost magnetnega polja sorazmerna z magnetnim trenutkom. Upoštevajte, da se intenzivnost polja zmanjšuje s kocko na daljavo.

Ta pristop je uporaben za katero koli zanko, dokler x biti velik v primerjavi z njenimi dimenzijami.

In ker linije tega polja spominjajo na tiste iz magneta, je enačba dober model za to magnetno polje in za druge sisteme, katerih linije so podobne, na primer: na primer:

Vam lahko služi: absorbanca: kaj je, primeri in vaje rešene

-Delci, naloženi v gibanju kot elektron.

-Atom.

-Zemlja in drugi planeti in sateliti sončnega sistema.

-Zvezde.

Vpliv zunanjega polja na zanko

Zelo pomembna značilnost magnetnega trenutka je njegova povezava do navora, ki ga ima zanka v prisotnosti zunanjega magnetnega polja.

Električni motor vsebuje tuljave, skozi katere poteka tok spreminjajoče se smeri in to zaradi zunanjega polja doživlja učinek obračanja. Ta zavoj se premika osi in električna energija med postopkom postane mehanska energija.

Navor na pravokotni zanki

Recimo, da bi olajšali izračune, pravokotne strani do in b, čigar običajni vektor n, odhodni zaslon, sprva je pravokotno na enakomerno magnetno polje B, Kot na sliki 3. Strani sile izkušenj zanke, ki jih daje:

F = IL x B

Kje L To je vektor magnitude, enak dolžini segmenta in usmerjen v skladu s tokom in je intenzivnost istega in B To je polje. Sila je pravokotna na oba L Kot na terenu, vendar ne vse strani doživljajo moč.

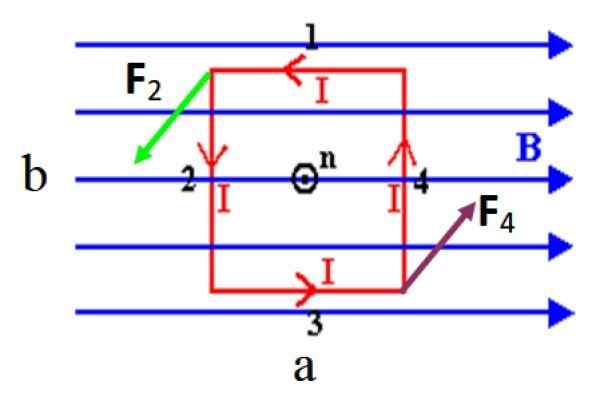Slika 3. Pravokotna spirala, ki v proti -ogrodnem smislu prevaža tok I, doživi navor v prisotnosti enotnega enotnega magnetnega polja. Vir: f. Zapata.

Na prikazani sliki na kratkih straneh 1 in 3 ni moči, ker sta vzporedna s poljem, ne pozabite, da je navzkrižni izdelek med vzporednimi vektorji ničen. Vendar dolga stran 2 in 4, ki sta pravokotna na B, Doživljajo sile, ki so označene kot F₂ in F₄.

Te sile tvorijo par: Imajo enako velikost in smer, vendar nasprotna čutila, zato se na sredini polja ne morejo premakniti v zanko. Vendar se lahko vrtijo, saj navor  τ Da vsaka sila izvaja navpično osi, ki poteka skozi sredino zanke, ima isto smer in pomen.

Vam lahko služi: kohezijska sila

V skladu z definicijo navora, kje r To je vektor položaja:

τ = r x F

Tako:

τ₂ = τ₄=(A/2) f (+J )

Posamezni navori niso preklicani, saj imajo isto smer in pomen, potem so dodani:

τ_mreža = τ₂ + τ₄ = a f (+J )

In ker je velikost sile f = ibb, je posledica:

τ_mreža = I⋅A⋅B⋅B (+J )

Produkt A⋅B je območje A v razmiku, zato je IAB velikost magnetnega trenutka μ. Zato τ_mreža = μ⋅B (+J )

Vidimo, da na splošno navor sovpada z vektorskim izdelkom med vektorji μ in B:

τ_mreža = μ x B

In čeprav je bil ta izraz izpeljan iz pravokotne zanke, velja za poljubno ravnanje.

Učinek polja na zanko je navor, ki teži k poravnavi magnetnega trenutka s poljem.

Potencialna energija magnetnega dipola

Če želite obrniti spiralo ali dipol na sredini polja, je treba opraviti delo proti magnetni sili, ki spreminja potencialno energijo Dipolo. Sprememba energije ΔU, ko se spirala vrti iz kota θ_tudi Pod kotom θ daje integral:

Če je referenčna raven izbrana za θ_tudi = π/2:

ΔU = -μB cos θ

Ki se lahko izraža kot skalarni izdelek med vektorji B in μ:

ΔU = - μ ·B

Najmanjša potencialna energija v dipolu se pojavi, ko cos θ = 1, kar to pomeni μ in B So vzporedni, energija je največja, če je nasprotna (θ = π) in je nična, če so pravokotna (θ = π/2).

Reference

1. Figueroa, d. 2005. Serija: Fizika za znanost in inženiring. Zvezek 5. Elektromagnetizem. Uredil Douglas Figueroa (USB).
2. Resnick, r. 1999. Fizično. Vol. 2. 3. izd. v španščini. Continental uredništvo s.Do. od c.V.
3. Sears, Zemansky. 2016. Univerzitetna fizika s sodobno fiziko. 14. Ed. Zvezek 2. Pearson.
4. Serway, r., Jewett, J. (2008). Fizika za znanost in inženiring. Zvezek 2. 7. Ed. Cengage učenje.
5. Tipler, str. (2006) Fizika za znanost in tehnologijo. 5. izd. Zvezek 2. Uredništvo se je vrtelo.