Politične značilnosti, aplikacije in primeri

A Politični proces Gre za termodinamični proces, ki se pojavi, ko je razmerje med pritiskom Str in glasnost V dobiti od Str.Vⁿ Ostane konstantno. Eksponent n To je resnično število, na splošno med ničlo in neskončnostjo, vendar je v nekaterih primerih lahko negativno.

Vrednost n Prejmite ime Politični indeks In pomembno je poudariti, da mora med politropskim termodinamičnim postopkom omenjeni indeks vzdrževati fiksno vrednost, sicer se postopek ne bo štelo za politropsko.

Slika 1. Značilna enačba politropnega termodinamičnega procesa. Vir: f. Zapata.

[TOC]

Značilnosti politropnih procesov

Nekateri značilni primeri politropnih procesov so: 

- Izotermalni postopek (pri konstantni temperaturi t), v katerem je eksponent n = 1.

- Izobarični postopek (konstantni tlak P), v tem primeru n = 0.

- Izokorični proces (do konstante volumna V), za katerega je n =+∞.

- Adiabatski procesi (do konstantne entropije), v katerih je eksponent n = γ, ki je γ adiabatska konstanta. Ta konstanta je količnik med toplotno zmogljivostjo pri konstantnem tlaku CP, deljeno s toplotno zmogljivostjo pri konstantni volumnu CV:

γ = CP/CV

- Kateri koli drug termodinamični postopek, ki ni kateri od prejšnjih primerov. Ampak skladno Str.Vⁿ = ctte Z resničnim in konstantnim politropnim indeksom n To bo tudi politropni postopek.

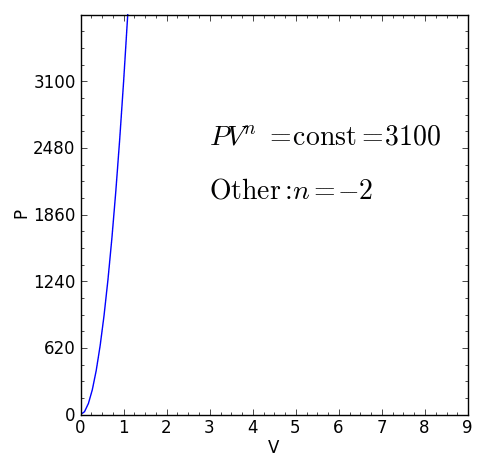Slika 2. Različni značilni primeri politropskih termodinamičnih procesov. Vir: Wikimedia Commons.

Prijave

Ena glavnih aplikacij politropske enačbe je za izračun dela, ki ga opravi zaprti termodinamični sistem, ko prehaja iz začetnega stanja v drug konca na kvazistatični način, torej po nasledstvu ravnotežnih stanj.

Delo v politropskih procesih za različne vrednosti n

Za n ≠ 1

Mehansko delo, ki ga izvaja zaprti termodinamični sistem, se izračuna z izrazom:

W = ∫p.DV

Vam lahko služi: diamagnetizem: materiali, aplikacije, primeri

Kjer je p tlak in v volumen.

Kot v primeru politropnega procesa je razmerje med tlakom in prostornino:

Str.V ⁿ = konstanta = c

Čiščenje P prejšnjega izraza, da ga nadomestite pri izražanju dela:

P = c /V ⁿ

Imate mehansko delo med politropnim postopkom, ki se začne v začetnem stanju 1 in konča v končnem stanju 2. Vse to se pojavi v naslednjem izrazu:

Če n ≠ 1, potem imate:

Poleg tega, ker sta začetna in končna stanja dobro opredeljena, je konstanta določena tudi z naslednjim izrazom:

C = str₁ V₁ⁿ = P₂ V₂ⁿ

Z zamenjavo vrednosti konstante pri izražanju dela dobimo:

W = (str₂ V₂ - Str₁ V₁)/(1-n)

V primeru, da je delovno snov modelirano kot idealen plin, je naslednja državna enačba:

Str.V = m.R.T

Kjer je m število molov idealnega plina in r je univerzalna konstanta plinov.

Za idealen plin, ki sledi politropnemu procesu z indeksom politropije, ki se razlikuje od enote in ki prehaja iz stanja z začetno temperaturo t₁ v drugo stanje s temperaturo t₂ Delo je podano z naslednjo formulo:

W = m r (t₂ - T₁)/(1-n)

Za n → ∞

V skladu s formulo za delo, pridobljeno v prejšnjem razdelku, je delo politropnega procesa z n = ∞ NULL, ker je izražanje dela razdeljeno med neskončnostjo, zato se rezultat ponavadi na nič.

Drug način, da dosežete ta rezultat₁ V₁ⁿ = P₂ V₂ⁿ, ki je mogoče napisati na naslednji način:

(P₁/P₂) = (V₂/V1)ⁿ

Če vzamete korenino N-zgoljca v vsakem članu, dobite:

(V₂/V1) = (p₁/P₂)^(1/n)

V primeru, da je n → ∞, morate (v₂/V1) = 1, kar pomeni, da:

Vam lahko služi: cedirana toplota: formule, kako jo izračunati in rešiti vaje

V₂ = V₁

To pomeni, da se prostornina v politropskem procesu ne spreminja z n → ∞. Zato je diferencial volumna DV v integralu mehanskega dela 0. Te vrste politropnih procesov so znane tudi kot procesi izokorično, o Procesi pri konstantni glasnosti.

Za n = 1

Spet imamo izraz za delo:

W = ∫p DV

V primeru politropnega procesa z n = 1 je razmerje med tlakom in prostornino:

P v = konstanta = c

Z čiščenjem P prejšnjega izraza in zamenjavo opravite delo, da prehajate iz začetnega stanja 1 v končno stanje 2:

W = ∫12P DV = CTTE ∫12 V^( - 1) DV = CTTE (ln (v2) - ln (v1))

To pomeni:

W = c ln (v₂/V₁).

Ker sta začetna in končna stanja dobro določena, bo tudi CTTE. To pomeni:

C = str₁ V₁ = P₂ V₂

Končno so na voljo naslednji uporabni izrazi za iskanje mehanskega dela poliitropnega zaprtega sistema, v katerem je n = 1.

W = p₁ V₁ ln (v₂/V₁) = P₂ V₂ ln (v₂/V₁)

Če delovna snov sestavlja m Moli idealnega plina, potem je mogoče uporabiti idealno enačbo plina: p v = m.R.T.

V tem primeru, kot je P.V₁ = CTTE, politropni postopek z n = 1 je postopek pri konstantni temperaturi t (izotermalno), tako da je mogoče dobiti naslednje izraze za delo:

W = m r t₁ ln (v₂/V₁) = m r t₂ ln (v₂/V₁)

Slika 3. Karambansko taljenje, primer izotermalnega procesa. Vir: Pixabay.

Primeri politropnih procesov

- Primer 1

Predpostavite valj s premičnim batom, polno s kilogramom zraka. Sprva zrak zaseda zvezek V₁= 0,2 m³ ob tlaku p₁= 400 kPa. Sledi politropni postopek z n = γ = 1,4, katerega končno stanje ima tlak₂ = 100 kPa. Določite delo, ki ga opravi zrak na batu.

Rešitev

Ko je indeks politropije enak adiabatski konstanti, obstaja postopek, v katerem delovna snov (zrak) ne izmenja toplote z okoljem in zato ne spremeni entropije.

Lahko vam služi: tretji zakon termodinamike: formule, enačbe, primeri

Za zrak, idealen diatomični plin, imate:

γ = CP/CV, s CP = (7/2) R in CV = (5/2) R

Tako:

γ = 7/5 = 1,4

Z izražanjem politropnega procesa lahko določimo končni volumen zraka:

V₂ = [P₂ V₁^1.4)/P₂]^(1/1.4) = 0,54 m³.

Zdaj obstajajo pogoji za uporabo delovne formule, narejene v politropskem postopku za n ≠ 1, pridobljeno zgoraj:

W = (str₂ V₂ - P1 v1)/(1-n)

Zamenjava ustreznih vrednosti je:

W = (100 kPa 0,54 m³ - 400 kPa 0,2 m³)/(1 - 1,4) = 65,4 kJ

- Primer 2

Predpostavimo isti valj iz primera 1, s premičnim batom, polnim s kilogramom zraka. Sprva zrak zaseda volumen V1 = 0,2 m³ pri tlaku p1 = 400 kPa. Toda za razliko od prejšnjega primera se zrak izotermično razširi, da doseže končni tlak P2 = 100 kPa. Določite delo, ki ga opravi zrak na batu.

Rešitev

Kot smo že videli, so izotermalni procesi politropni procesi z indeksom n = 1, zato je izpolnjeno:

P1 v1 = p2 v2

Na ta način je mogoče končni obseg enostavno odpraviti, da dobimo:

V2 = 0,8 m³

Nato je z izrazom predhodno pridobljenega dela za primer n = 1 delati z zrakom na batu v tem postopku:

W = p1 v1 ln (v2/v1) = 400000 pa × 0,2 m³ ln (0,8/0,2) = 110,9 kJ.  

Reference

1. Bauer, w. 2011. Fizika za inženiring in znanosti. Zvezek 1. MC Graw Hill.
2. Cengel in. 2012. Termodinamika. 7. izdaja. McGraw Hill.
3. Figueroa, d. (2005). Serija: Fizika za znanost in inženiring. Zvezek 4. Tekočine in termodinamika. Uredil Douglas Figueroa (USB).
4. López, c. Prvi zakon termodinamike. Okrevano od: Culturacienta.com.
5. Vitez, r. 2017. Fizika za znanstvenike in inženiring: strateški pristop. Pearson.
6. Serway, r., Vulle, c. 2011. Osnove fizike. 9na ed. Cengage učenje.
7. Univerza Sevilla. Termični stroji. Okreval od: laplace.nas.je.
8. Wikiwand. Politični proces. Okreval od: wikiwand.com.