Unidimenzionalni valovi matematični izraz in primeri

The Enodimenzionalni valovi Oni so tisti, ki se širijo v eno smer, ne glede na to, ali se vibracije pojavljajo ali ne v isti smeri širjenja. Dober primer od njih je val, ki se premika po napeti vrvi, kot je kitara.

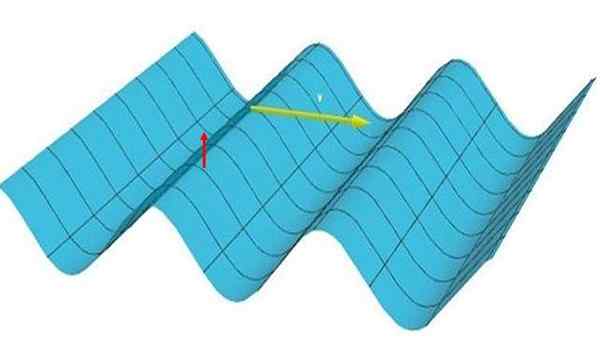
V ravnem valu križ, Delci vibrirajo navpično (vzpenjajo se in se spustijo, na sliki 1 zagledajo rdečo puščico), vendar je ena -dimenzionalna, ker motnje potujejo v eno smer, po rumeni puščici.

Slika 1: Slika predstavlja eno -dimenzijski val. Upoštevajte, da grebeni in doline tvorijo vzporedne črte med seboj in pravokotno na smeri širjenja. Vir: Self Made.

Edinimenzionalni valovi se v vsakdanjem življenju pojavljajo precej pogosto. V naslednjem razdelku je opisano nekaj primerov le -teh in tudi valov, ki niso enoidimenzionalni, da jasno ugotovijo razlike.

[TOC]

Primeri enoidimenzionalnih valov in neenidimenzionalnih valov

Enodimenzionalni valovi

To je nekaj primerov enega -dimenzionalnih valov, ki jih je mogoče enostavno opaziti:

- Zvočni utrip, ki potuje skozi ravno palico, saj je to motnjo, ki se širi po palici.

- Val, ki potuje skozi vodni kanal, tudi če premik vodne površine ni vzporeden s kanalom.

- Valovi, ki se širijo na površini ali skozi tridimenzionalni prostor, so lahko tudi eno -dimenzionalni, pod pogojem, da so njihove valovne fronte ravnine vzporedne med seboj in potujejo v eno smer.

Nedimenzionalni valovi

Primer nedimenzionalnega vala najdemo v valovih, ki nastanejo na površini mirno vodo, ko se kamen spusti. Je dvodimenzionalna valovna sprednja stran cilindričnega vala.

Vam lahko služi: ročna ročicaSlika 2. Slika predstavlja primer tega, kar ni eno -dimenzijski val. Upoštevajte, da grebeni in doline tvorijo kroge, smer širjenja pa je radialna navzven, nato pa je dvodimenzionalni krožni val. Vir: Pixabay.

Drug primer ne-sindikalnega dimenzijskega vala je zvočni val, ki ustvarja petardo z eksplozijo na določeni višini. To je tridimenzionalni val s sferičnimi valovnimi frontami.

Matematični izraz eno -dimenzionalnega vala

Najbolj splošen način izražanja eno -dimenzionalnega vala, ki se širi brez slabljenja v pozitivni smeri osi x in s hitrostjo v To je matematično:

in (x, t) = f (x - v.T)

V tem izrazu in predstavlja motnjo v položaju x Takoj t. Valovna oblika daje funkcija F. Na primer, valovna funkcija, prikazana na sliki 1, je:  in (x, t) = cos (x - v t) in slika vala ustreza trenutku t = 0.

Pokliče se takšen val, ki ga opisuje kosinusna ali sinusna funkcija harmonični val. Čeprav ni edina valovna oblika, ki obstaja, je izjemnega pomena, saj je mogoče kateri koli drug val predstaviti kot prekrivanje ali vsoto harmoničnih valov. To je znanec Fourier teorem, Tako se uporablja za opis signalov vseh vrst.

Ko val potuje v negativni smeri osi x, se preprosto spremeni v mimo -v V argumentu, biti:

in (x, t) = g (x + v t)

Slika 3 prikazuje animacijo vala, ki potuje na levo: je oblika, imenovana funkcija Lorentziana in ona Matematični izraz je:

Vam lahko služi: delo: formula, enote, primeri, vaje

in (x, t) = 1 / (1 + (x + 1⋅T)²

V tem primeru je hitrost širjenja v = 1, -enota prostora za vsako enoto časa-.

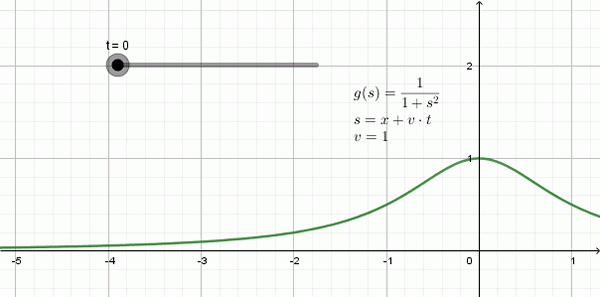Slika 3. Primer Lorentzijevega vala, ki hitro potuje na levo V = 1. Vir: Pripravil F. Zapata z geogebro.

Unidimenzionalna enačba valov

Enačba valov je enačba v delnih derivatih, katerih rešitev je seveda val. Vzpostavi matematični odnos med prostorskim delom in njegovim časovnim delom ter ima obliko:

Rešitev, ki je natančno funkcija y (x, t), je mogoče preveriti z zamenjavo in razvojem v tej enačbi. Na primer funkcije f (x - v t)  in  G (x + vt)  omenjeno, so rešitve za enačbe valov.

Rešen primer

Potem imate splošni izraz y (x, t) za harmonični val:

in (x, t) = a⋅cos (k⋅x ± ω⋅T + θo)

a) Opišite fizični pomen parametrov A, k, Ω in θo.

b) Kakšen pomen imajo znake ± o argumentu Coseno?

c) Preverite, ali je dani izraz res rešitev valovne enačbe prejšnjega odseka in poiščite hitrost v širjenja.

Rešitev)

Značilnosti vala so v naslednjih parametrih:

-Do predstavlja amplituda ali "višina valov".

-k je v Valovna številka In je povezan z valovno dolžino λ skozi K = 2π/ λ.

-Ω Je fkotna ekspanzija In je povezan z obdobje T valovno nihanje s

Ω = 2π/ t.

-θo Je začetna faza, ki je povezan z izhodiščem vala.

Vam lahko služi: statično trenje: koeficient, primer, vaja

Rešitev B)

Če val potuje v pozitivni smeri osi x in pozitivnega znaka, se negativni znak.

Rešitev C)

Preverite, ali je dani izraz rešitev za enačbo valov preprost: delni derivat funkcije in (x, t) Kar zadeva X dvakrat, delno izhaja iz T dvakrat, nato pa se oba rezultata srečata, da dobita enakost:

Drugi izhaja iz x: ∂²in/ ∂x²= -K². Do⋅cos (k⋅x ± ω⋅T + θo)

Drugi izhaja iz T: ∂²in/ ∂t²= -Ω². Do⋅cos (k⋅x ± ω⋅T + θo)

Ti rezultati se nadomestijo v valovni enačbi:

 -k². Do⋅cos (k⋅x ± ω⋅t + θo) = (1/v²) (-Ω². Do⋅cos (k⋅x ± ω⋅T + θo))

Zelo Do Ker je kosinus poenostavljen, saj se pojavljajo na obeh straneh enakosti in je argument kosinusa enak, zato se izraz zmanjša na:

-k² = (1/v²) (-Ω²)

Ki omogoča pridobitev enačbe v v smislu Ω in k:

v² = Ω² / k²

v = ± Ω / k

Reference

1. E-izobraževalni. Enačba enoidimenzionalnih harmoničnih valov. Okrevano od: e-ducative.Katedu.je
2. Rincón fizike. Valovni razredi. Pridobljeno iz: fizike.Blogspot.com.
3. Figueroa, d. 2006. Valovi in ​​kvantna fizika. Serija: Fizika za znanost in inženiring. Uredil Douglas Figueroa. Univerza Simon Bolivar. Caracas Venezuela.
4. Physics Lab. Valovno gibanje. Okreval od: fisicalbab.com.
5. Peirce, a. Predavanje 21: Enodimenzionalna valovna enačba: D'Alembertova rešitev. Pridobljeno iz: UBC.AC.
6. Valovna enačba. Pridobljeno iz: v.Wikipedija.com