Stacionarne valove formule, značilnosti, vrste, primeri

The stoječi valovi So valovi, ki se širijo v omejeni polovici, gredo v del prostora, za razliko od potujočih valov, ki se pri širjenju odmikajo od vira, ki je nastal.

So osnova zvokov, ki nastanejo v glasbil, saj zlahka nastajajo na fiksnih strunah, bodisi na enem od njegovih koncev ali obojega. Ustvarjajo se tudi v napetih membranah, kot so bobni ali notranje cevi in ​​strukture, kot so mostovi in ​​zgradbe.

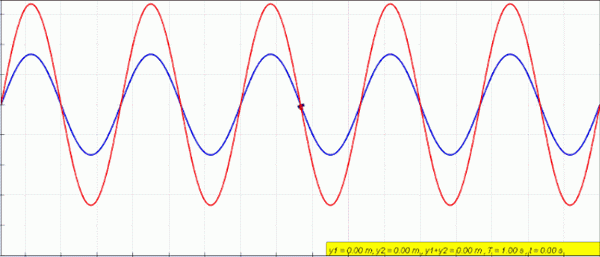Animacija stacionarnega (rdečega) vala, ki ga ustvari superpozicija levega (modrega) in desnega vala (zelena). Vir: Lookangmany Zahvaljujoč avtorju originalne simulacije = Wolfgang Christian in Francisco Shembre avtorja Easy Java Simulacije = Francisco Shembre/CC BY-SA (https: // CreativeCommons.Org/licence/by-sa/4.0

Ko imate na obeh koncih fiksno vrv, na primer kitara, so valovi ustvarjeni z enako amplitudo in frekvenco, ki potujejo v nasprotnih čutilih in združujejo, kar ustvarja pojav, imenovan vmešavanje.

Če so valovi v fazi, so grebeni in doline poravnani in povzročijo val z dvojno amplitudo. V tem primeru govori o konstruktivnem vmešavanju.

Če pa valovi, ki se vmešavajo, niso v fazi, grebeni enega ustrezajo dolinam drugih in amplituda, ki je rezultat. To je potem uničujoč vmes.

[TOC]

Formule in enačbe

Glavni elementi vala, ki ga predstavljajo v prostoru in času, so njegova amplituda A, njegova valovna dolžina λ in njegova kotna frekvenca Ω.

Elementi vala. Vir: Wikimedia Commons.

V matematični reprezentaciji je raje uporabljati K kot Valovna številka o Številnikrat se dogaja val na enoto. Zato je opredeljen skozi dolžino λ vala, ki je razdalja med dvema dolinama ali dvema grebenama:

K = 2π/ λ

Medtem ko kotna frekvenca Povezana je z obdobjem ali trajanjem popolnega nihanja, kot je:

Ω = 2π/ t

In tudi frekvenca f je podana z:

F = ω / 2π

Zato:

F = 1/t

Poleg tega se valovi premikajo s hitrostjo v po navedbah:

v = λ.F

Matematični izraz stacionarnega vala

Matematično lahko izrazimo val skozi sinusno funkcijo ali kosinusno funkcijo. Recimo, da obstajajo valovi enake amplitude A, valovne dolžine λ in frekvence Ω, ki se širijo po vrvi in ​​v nasprotnih čutilih:

in₁ = Greh (kx - ωt)

in₂ = A greh (kx + ωt)

Ko jih dodajamo, najdemo nastali val in_R:

in_R = y₁ + in₂ = A Sen (kx - ωt) + a greh (kx + ωt)

Obstaja trigonometrična identiteta za iskanje vsote:

Vam lahko služi: kaj je relativno in absolutno hrapavost?

sin α + sin β = 2 sin (α + β)/2 . cos (α - β)/2

Skozi to identiteto, nastali val in_R je ostalo:

in_R = [2A Sen KX] . cos ωt

Lokacija vozlišč in trebuha

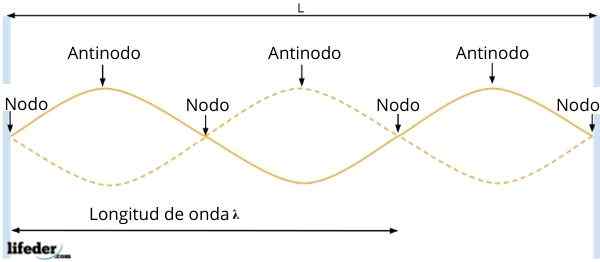Antinodos ali trebuh in vozlišča

Nastali val ima amplitudo_R = 2ase KX, ki je odvisen od položaja delca. Nato se na točkah, za katere je Sen KX = 0, amplituda vala prekliče, torej ni vibracij.

Te točke so:

Kx = π, 2π, 3π ..

Kot k = 2 π/ λ:

(2 π/ λ) x = π, 2π, 3π ..

x = λ/2, λ, 3λ/2 ..

V takšnih točkah pride do uničevalnih motenj in se imenujejo vozlišča. Ločeni so za razdaljo, ki je enaka λ/2, kot je bilo sklenjeno iz prejšnjega rezultata.

In med dvema zaporednima vozliščema sta antinodos oz trebuh, v katerem je amplituda vala največja, saj se pojavijo konstruktivne motnje. Se pojavijo, ko:

sin kx = ± 1

Kx = ± π/2, 3π/2, 5π/2 ..

Spet k = 2 π/ λ in nato:

x = λ /4, 3λ /4, 5λ /4, ..

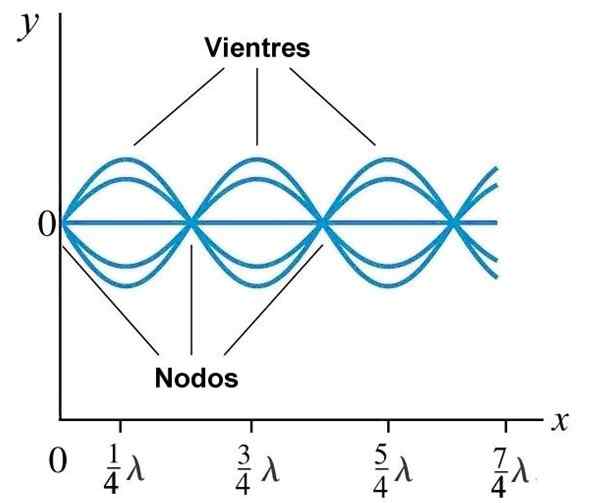Trebuh ali antinode in vozlišča v stacionarnem valu, ustvarjenem na vrvi s fiksnim koncem pri x = 0. Vir: Wikimedia Commons.

Običajni načini na vrvi

Obmejni pogoji na vrvi določajo, kako so valovne dolžine in frekvence. Če je vrv v dolžini l pritrjen za dva konca, ne more vibrirati s frekvenco, ker so točke, kjer je vrv pritrjena, že vozlišča.

Poleg tega je ločitev med sosednjimi vozlišči λ/2, med vozliščem in trebuhom :

(λ/2) = l, z n = 1, 2, 3, 4 .. .

Zato:

λ = 2L/n

Harmonike

Poimenujejo se različne vrednosti λ harmonike. Tako imamo:

-Prva harmonika: λ = 2l

-Druga harmonika: λ = l

-Tretja harmonika: λ = 2 l/3

-Harmonična soba: λ = l/2

In tako naprej.

Hitrost in frekvenca

Čeprav se zdi, da se stacionarni val ne premika, je enačba še vedno veljavna:

v = λ. F

Zato:

v = (2l/n) . F

F = nv/2l

Zdaj je mogoče dokazati, da je hitrost, s katero se val premika v vrvi, odvisna od napetosti T v isti in njene linearne gostote mase μ (masa na enoto dolžine) kot:

Zato:

Vam lahko služi: mrtve obremenitve: značilnosti, izračun, primeri

Značilnosti stacionarnih valov

-Ko so valovi nepremični, se dobljeni val ne širi kot njene komponente, ki gredo iz enega kraja v drugega. Obstajajo točke, kjer y = 0, ker ni vibracij: vozlišča, z drugimi besedami, amplituda do_R Je nič.

-Matematični izraz stacionarnega vala je sestavljen iz produkta prostorskega dela (ki je odvisen od koordinate X ali prostora) in časovnega dela.

-Med vozlišči nastali črni val na enem mestu niha, medtem ko so valovi, ki gredo iz enega kraja v drugo, zastareli.

-Ravno v vozliščih se energija ne prevaža, saj je to sorazmerno s kvadratom amplitude, vendar je ujeti med vozlišči.

-Razdalja med sosednjimi vozlišči je polovica valovne dolžine.

-Točke, na katerih je pritrjena vrv, veljajo tudi za vozlišča.

Fantje

Stacionarni valovi v dimenziji

Valovi v fiksni vrvi so primeri stacionarnih valov v dimenziji, katerih matematični opis smo ponudili v prejšnjih razdelkih.

Stacionarni valovi v dveh in treh dimenzijah

Stacionarne valove je mogoče predstaviti tudi v dveh in treh dimenzijah, kar je nekoliko bolj zapleten matematični opis.

Primeri dirkalnih ONDAS

Fiksne strune

-Niz, ki ga pritrdi ekstrem, ki ga nihala z roko ali z enim batom, drugi ustvari stacionarne valove po svoji dolžini.

Glasbila

Stacionarni valovi nastajajo v glasbilskih inštrumentih, kot je Violoncello. Vir: Pixabay.

-Ko igrate godalne instrumente, kot so kitara, harfa, violina in klavir.

STLOVER valovi nastajajo tudi v zračnih ceveh, kot so organske cevi.

Stavbe in mostove

Stacionarni valovi nastanejo v strukturah, kot so mostovi in ​​stavbe. Izjemen primer je bil viseči most Tacoma v bližini mesta Seattle v ZDA. Kmalu po odprtju leta 1940 se je ta most zrušil zaradi nepremičnih valov, ustvarjenih v vetru.

Frekvenca vetra se je ujemala z naravno frekvenco mostu, ki je v tem ustvarjala v stacionarnih valovih, ki so povečali njihovo amplitudo, dokler se most ni zrušil. Pojav je znan kot resonanca.

Lahko vam služi: svetlobni odsev

Seiches

V pristaniščih se imenuje zelo radoveden pojav Seiche, v katerem valovi morja proizvajajo velika nihanja. To je zato, ker so vode v pristanišču precej zaprte, čeprav oceanske vode tako pogosto prodrejo skozi vhod v pristanišče.

Port Waters se giblje s svojo frekvenco, pa tudi s tistimi v oceanu. Če se obe vodi ujemata z njihovimi frekvencami, je zaradi resonance velik stacionarni val, kot se je zgodilo z mostom Tacoma.

The Seiches Pojavijo se lahko tudi v jezerih, rezervoarjih, bazenih in drugih vodnih telesih, omejenih s površinami.

Ribje rezervoarje

Stacionarne valove je mogoče ustvariti v ribji robu, ki ga prenaša oseba, če je frekvenca, s katero je oseba enaka frekvenci nihanja vode.

Vaja rešena

Kitarska vrv ima l = 0.9 m in linearna gostota testa μ = 0.005 kg/m. Je podvržen 72 n napetosti, njegov način vibracije pa je tisti, ki prikazuje sliko z amplitudo 2A = 0.5 cm.

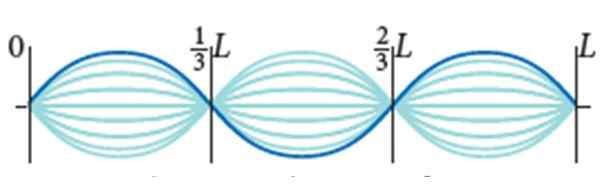Stacionarni valovi na kitarni vrvi. Vir: Bauer, W. Fizično.

Najti:

a) hitrost širjenja

b) valovna frekvenca

c) ustrezna enačba stacionarnega vala.

Rešitev

Skozi:

Je pridobljen;

V = [72 n/(0.005 kg/m)]^1/2  = 120 m/s.

Rešitev b

Razdalja med dvema sosednjima vozliščema je λ/2, torej:

(2/3) l - (1/3) l = λ/2

(1/3) l = λ/2

λ = 2l/3 = 2 x 0.90 m / 3 = 0.60 m.

Kot v = λ.F

F = (120 m/ s)/ 0.60 m = 200 s^-1= 200 Hz.

Rešitev c

Enačba je:

in_R = [2A Sen KX] . cos ωt

Zamenjati moramo vrednosti:

K = 2π/ λ = k = 2π/ 0.60 m = 10 π/3

F = ω / 2π

Ω = 2π x 200 Hz = 400 π Hz.

Amplituda 2A že daje izjavo:

2a = 0.5 cm = 5 x 10 ^-3 m.

Zato:

in_R = 5 x 10 ^-3 m . greh [(10π/3) x] . cos (400πt) =

= 0.5 cm . greh [(10π/3) x] . cos (400πt)

Reference

1. Bauer, w. 2011. Fizika za inženiring in znanosti. Zvezek 1. MC Graw Hill.
2. Figueroa, d. (2005). Serija: Fizika za znanost in inženiring. Zvezek 7. Valovi in ​​kvantna fizika. Uredil Douglas Figueroa (USB).
3. Giancoli, d.  2006. Fizika: načela z aplikacijami. 6. Ed Prentice Hall.
4. Serway, r., Jewett, J. (2008). Fizika za znanost in inženiring. Zvezek 1. 7. Ed. Cengage učenje.
5. Tipler, str. (2006) Fizika za znanost in tehnologijo. 5. izd. Zvezek 1. Uredništvo se je vrtelo.
6. Wikipedija. Seiche. Okrevano od: je.Wikipedija.org.