Značilnosti senoidnih valov, deli, izračun, primeri

The Sinusni valovi So vzorci valov, ki jih lahko matematično opišejo sinusne in kosinusne funkcije. Pravilno opisujejo naravne dogodke in spremenljive znake v času, kot so napetosti, ki jih ustvarjajo električne rastline, nato pa se uporabljajo v domovih, panogah in ulicah.

Električni elementi, kot so upori, kondenzatorji in induktivnosti, ki se povezujejo z vhodi sinusoidne napetosti, ustvarjajo tudi odgovore tudi sinusoidni. Matematika, uporabljena v njihovem opisu, je razmeroma preprosta in je bila temeljito preučena.

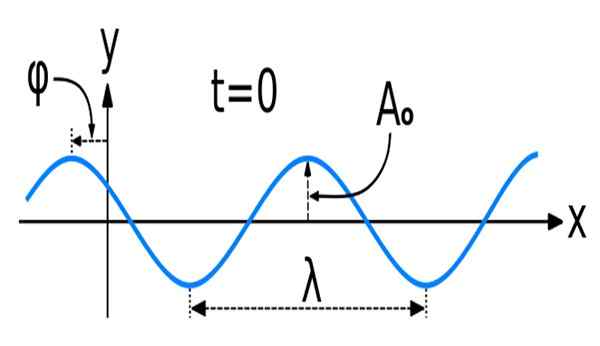
Slika 1. Sinusni val z nekaterimi glavnimi prostorskimi značilnostmi: amplituda, valovna dolžina in faza. Vir: Wikimedia Commons. Val_new_sine.SVG: Kraaiennestoriginalno ustvarjen kot kosinus.SVGDEVATIVNO DELO: DAVE3457 [CC BY-SA 3.0 (https: // creativeCommons.Org/licence/by-sa/3.0)]

Matematika sinusoidnih ali sinusoidnih valov, kot so tudi znani, je funkcija sinusa in kosinusa.

To so ponavljajoče se funkcije, kar pomeni periodičnost. Oba imata enako, s pogojem, da je kosinus razseljen na levo glede na dojko v kolesarski sobi. Opazimo na sliki 2:

Slika 2. Funkcije Sen X in Cos X so razseljene glede na drugo. Vir: f. Zapata.

Potem cos x = sin (x + π/2). S pomočjo teh funkcij je predstavljen sinus. Če želite to narediti, je zadevna velikost postavljena na navpično osi, medtem ko se na vodoravni osi čas nahaja.

Na zgornjem grafu je cenjena tudi ponavljajoča se kakovost teh funkcij: vzorec se ponavlja neprekinjeno in redno. Zahvaljujoč tem funkcijam lahko izražate napetosti in tokove sinijskega tipa, ki se sčasoma razlikujejo in postavite na navpično osi namesto na in, a v ali eno Yo predstavljati napetost ali tok in na vodoravni osi namesto x, The t vreme.

Najbolj splošen način izražanja sinusnega vala je:

v (t) = v_m greh (ωT+φ)

Nato bomo poglobili pomen tega izraza in opredelili nekaj osnovnih izrazov, da bi označili sinus.

[TOC]

Zabave

Obdobje, amplituda, frekvenca, cikel in faza se koncepti uporabljajo za periodične ali ponavljajoče se valove in so pomembni za njihovo pravilno karakterizacijo.

Obdobje

Periodična funkcija, kot je omenjena, ki se ponavlja v rednih presledkih, vedno ustreza naslednji lastnini:

f (t) = f (t + t) = f (t + 2T) = f (t + 3t) =… .

Kje T To je znesek, imenovan val, In čas je, da ponovimo fazo istega. V mednarodnih sistemskih enotah se obdobje meri v sekundah.

Amplituda

Glede na splošno izražanje senoidnega vala v (t) = v_m greh (ωt+φ), v_m To je največja vrednost funkcije, ki se pojavi, ko greh (ωt+φ) = 1 (Če se spomnimo, da je največja vrednost, ki jo priznavata sinus in kosinus. Ta največja vrednost je natančno Amplituda valov, poznan tudi kot Amplituda največjega.

V primeru napetosti se meri v voltih in če je tok, bo v amperih. V sinusnem valu je širina konstantna, pri drugih vrstah vala pa se lahko amplituda razlikuje.

Vam lahko služi: termometer upora: značilnosti, delovanje, uporabe

Cikel

Je del vala, ki ga vsebuje obdobje. Na prejšnji sliki je bilo obdobje vzeto z merjenjem iz dveh zaporednih vrhov ali grebenov, vendar ga lahko začnemo meriti iz drugih delov vala, medtem ko so omejene z obdobjem.

Opomba na naslednji sliki, ko en cikel pokriva od ene točke v drugo z enako vrednostjo (višino) in istim naklonom (naklon).

Slika 3. V sinusnem valu se za nekaj časa vedno poteka cikel. Pomembno je, da sta izhodišče in konec na isti višini. Vir: Boylestad. Uvod v analizo vezja. Pearson.

Frekvenca

Količina ciklov se pojavi v 1 sekundi in je povezana z argumentom funkcije sinusa: ωt. Frekvenca je označena kot F In se meri v ciklih na sekundo ali Hertz (HZ) v mednarodnem sistemu.

Pogostost je torej obratna količina obdobja:

F = 1/t

Medtem ko frekvenca F je povezan z Kotna frekvenca ω (pulzacija) kot:

Ω = 2πF

Kotna frekvenca je izražena v radianih /Second v mednarodnem sistemu, vendar so radiani brezmenzionalni, torej frekvenca F in kotna frekvenca Ω Imajo enake dimenzije. Upoštevajte, da izdelek ωt kot rezultat daje radiane in jih je treba upoštevati pri uporabi kalkulatorja za pridobitev vrednosti Sen ωt.

Faza

Ustreza horizontalnemu premiku, ki ga doživlja val, glede na čas, ki je bil vzet kot referenca.

Na naslednji sliki je zeleni val v času napredoval glede na rdečo t_d. Dva sinusoidna vala sta faza Ko sta vaša frekvenca in faza enaka. Če se faza razlikuje, potem so v vrzel. Slika 2 valovi so tudi zastareli.

Slika 4. Pokukani sinusidni valovi. Vir: Wikimedia Commons. Noben strojno berljiv avtor ni zagotovil. Kanjo ~ Commonswiki je domneval (na podlagi zahtevkov za avtorske pravice). [Javna domena].

Če je frekvenca valov drugačna, bodo v fazi, ko bo faza ωt+φ biti enako v obeh valovih v določenih trenutkih.

Generator senoidnih valov

Obstaja veliko načinov za pridobitev sinusnega signala. Domači teki jim zagotavljajo.

Uporaba Faradayevega zakona

Preprost način za pridobitev sinusnega signala je uporaba Faradayevega zakona. To kaže, da se v zaprtem vezju toka, na primer zanke, nameščene na sredini magnetnega polja, ustvari inducirani tok, ko se magnetno polje skozi njega spreminja. Posledično a Inducirana napetost tudi inducirani fem.

Pretok magnetnega polja se razlikuje, če se zanka vrti s konstantno kotno hitrostjo na sredini polja, ustvarjenega med drogovi N in S.

Vam lahko služi: Neptun (planet)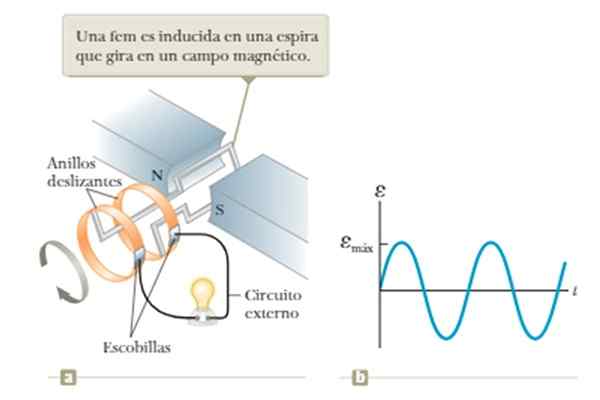Slika 5. Generator valov, ki temelji na indukcijskem zakonu Faraday. Vir: Vir: Raymond A. Serway, Jonh W. Jewett [cc by-sa 4.0 (https: // creativeCommons.Org/licence/by-sa/4.0)].

Omejitev tega operativca je odvisnost od napetosti, dobljene s frekvenco vrtenja zanke, kot bo podrobneje razvidno iz primera 1 oddelka za primere kasneje.

Wien Oscilator

Drug način za pridobitev sinusnega vala, tokrat z elektronom. Na ta način dobimo sinusni valovi, katerih frekvenca in amplituda se lahko uporabnik spremeni v skladu z njihovo udobje s prilagajanjem stikala.

Slika prikazuje sinusni generator signala, s katerim je mogoče dobiti tudi druge valovne oblike: trikotne in kvadratke med drugim.

Slika 6. Generator signala. Vir: Vir: Wikimedia Commons. OPGREG pri angleški Wikipediji [CC BY-SA 3.0 (https: // creativeCommons.Org/licence/by-sa/3.0)].

Kako izračunati sinusne valove?

Za izvajanje izračunov, ki vključujejo sinusne valove, se uporablja znanstveni kalkulator, ki ima sinusne in kosinusne trigonometrične funkcije, pa tudi njene inverzne. Ti kalkulatorji imajo načine za delo v kotih bodisi v stopinjah ali radianih, in enostavno je pretvoriti eno pot v drugo. Faktor pretvorbe je:

180 ° = π Radiani.

V skladu z modelom kalkulatorja se morate pomakati prek ključa načina, da poiščete možnost stopnje, ki vam omogoča delo na trigonometričnih funkcijah v stopinjah ali možnosti RAD, da neposredno delate kote v radianih.

Na primer sin 25 ° = 0.4226 s kalkulatorjem, vstavljeno v način DEG. S pretvorbo 25 ° v radiane dobite 0.4363 Radianes in Sen 0.4363 rad = 0.425889 ≈ 0.4226.

Osciloskop

Osciloskop je aparat, ki omogoča vizualizacijo na zaslonskih znakih napetosti in tokov, ki jih izmenično in neposredni. Ima gumbe za prilagoditev velikosti signala na mreži, kot je prikazano na naslednji sliki:

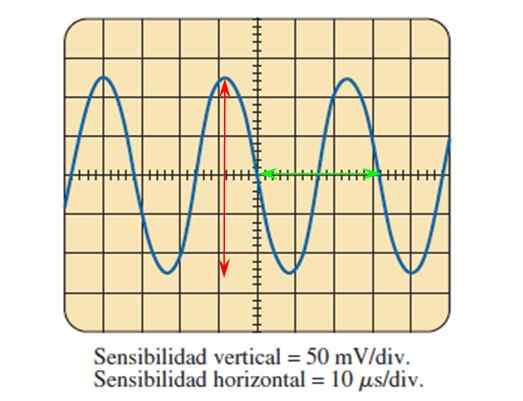Slika 7. Sinusoidni signal, izmerjen z osciloskopom. Vir: Boylestad.

S pomočjo slike, ki jo zagotavlja osciloskop, in poznavanje prilagajanja občutljivosti v obeh osi je mogoče izračunati zgoraj opisane parametre valov.

Vam lahko služi: eliptične galaksije: tvorba, značilnosti, vrste, primeri

Slika prikazuje sinusni napetostni signal kot funkcija časa, v katerem je vsaka delitev navpične osi vredna 50 milivoltov, medtem ko je v vodoravni osi vsaka delitev vredna 10 mikrosekundov.

Vrhunska amplituda najvišjega do vrha šteje delitve, ki jih val obsega navpično, in pomaga pri rdeči puščici:

5 oddelkov se šteje s pomočjo rdeče puščice, zato je napetost Peak-Pico:

V_pp = 5 oddelkov x 50 mV/delitve = 250 mV.

Pico napetost V_str Meri iz vodoravne osi, ki je 125 mV.

Če želite najti obdobje, se meri cikel, na primer tistega, ki ga ima zelena puščica, ki zajema 3.2 oddelki, potem je obdobje:

T = 3.2 oddelki x 10 mikrosekund/delitev = 32 mikrosekund = 32 μs

Primeri

Primer 1

Za generator na sliki 3 izkazujte iz Faradayevega zakona, da ima inducirana napetost sinus. Predpostavimo, da je zanka sestavljena iz N zavojev namesto enega, vse z istim območjem A in se na sredini magnetnega polja obrača s konstantno kotno hitrostjo Ω B enotna.

Rešitev

Faradayev zakon pravi, da inducirani fem ε je:

ε = -n (dφ_B /dt)

Kje Φ_B To je pretok magnetnega polja, ki bo spremenljiv, saj je odvisno od tega, kako je zanka izpostavljena vsakemu trenutku. Negativni znak preprosto opisuje dejstvo, da ta fem nasprotuje vzroku, ki ga proizvaja (Lenzov zakon). Pretok zaradi ene zanke je:

Φ_B = B.Do.cos θ

θ je kot, ki ga oblikuje običajni vektor do ravnine zanke s poljem B Ko poteka vrtenje (glej sliko), se ta kot seveda razlikuje kot:

θ = ωt

Tako da: Φ_B = B.Do.cos θ = b.Do.cos ωt. Zdaj morate ta izraz izpeljati glede na čas in z njim dobite inducirano FEM:

ε = -n.D (b.Do.cos ωt) /dt

Kot polje B Je enakomerna in območje spaze se ne razlikuje, zapustijo izpeljan:

ε = -nba. D (cos ωt) /dt = ωnba. Sen ωt

Primer 2

Zanka ima območje 0.100 m² in zavijte na 60.0 Rev/s, z osi vrtenja, pravokotno na enakomerno magnetno polje 0.200 t. Vedeti, da ima tuljava 1000 obratov za iskanje: a) največje ustvarjene FEM, b) orientacija tuljave glede na magnetno polje, ko se pojavi največja inducirana FEM.

Slika 8. Spirala n krogov, razbit na sredini enakomernega magnetnega polja in ustvari sinusni signal. Vir: r. Serway, fizika za znanost in inženiring. Zvezek 2. Cengage učenje.

Rešitev

a) Največja ženska je ε_Max = Ωnba

Preden nadaljujete z nadomeščanjem vrednosti, je treba sprejeti frekvenco 60 vrtljajev do enot mednarodnega sistema. Znano je, da je 1 revolucija enakovredna radianom zavoja ali 2p:

60.0 Rev/S = 120p Radianes/s

ε_Max = 120p Radianes x 1000 krogov x 0.200 t x 0.100 m² = 7539.82 V = 7.5 kV

b) Ko pride do te vrednosti Sen ωt = 1 Zato:

ωt = θ = 90 °,

V tem primeru je spiralna ravnina vzporedna B, tako da običajni vektor do omenjene ravnine tvori 90 ° s poljem. To se zgodi, ko je črni vektor na sliki 8 pravokoten na zeleni vektor, ki predstavlja magnetno polje.

Reference

1. Boylestad, r. 2011. Uvod v analizo vezja. 12. Izdaja. Pearson. 327-376.
2. Figueroa, d. 2005. Elektromagnetizem. Fizične serije za znanost in inženiring. Zvezek 6. Uredil d. Figueroa. Univerza Simon Bolivar. 115 in 244-245.
3. Figueroa, d. 2006. Fizični laboratorij 2. Uredništvo Equinox. 03-1 in 14-1.
4. Sinusni valovi. Okreval od: iessierradegara.com
5. Serway, r. 2008.Fizika za znanost in inženiring. Zvezek 2. Cengage učenje. 881-884