Kvantne številke za uporabo in kaj so

The nKvantni umters Uporabljajo se za opis kvantnega stanja elektronov v atomu in izvirajo iz raztopine Schrödingerjeve enačbe za najpreprostejše od vseh: vodik.

Schrödingerjeva enačba je diferencialna enačba, katere rešitve so Valovne funkcije in jih označuje grško pismo ψ. Neskončne rešitve je mogoče dvigniti, njegov kvadrat orbitalno.

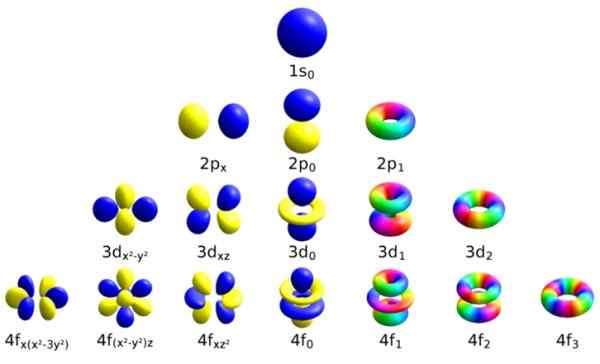
Vsako od teh atomskih orbital odlikuje določen sklop kvantnih številk. Vir: Wikimedia Commons.

Vsaka orbitala ima opredeljene značilnosti, ki jo razlikujejo od drugih, kot so energija, kotni zagon in vrtenje, v celoti kvantna lastnost elektrona in ki je med drugim odgovorna za magnetne učinke.

Način prepoznavanja vsake orbitale je, da ga ločite skozi niz števil, ki ga opisujejo, in to so natančno kvantne številke:

-N: je glavna kvantna številka.

-ℓ: Azimutalna kvantna številka.

-m_ℓ, To je magnetna številka.

-m_s, Številka spin.

[TOC]

Za kaj so kvantne številke?

Kvantne številke služijo za opis stanja elektronov znotraj atoma. Tisti atomski model, v katerem se elektron obrne okoli jedra, je netočen, ker ni skladen z atomsko stabilnostjo ali z velikim številom fizičnih pojavov.

Zato danski Niels Bohr (1885-1962) je leta 1913 podal drzen predlog: Elektron lahko najdemo le v določenih stabilnih orbitah, katerih velikost je odvisna od števila celoštevilčev, imenovane N.

Kasneje, leta 1925, je avstrijski fizični Erwin Schrödinger (1887-1961) dvignil diferencialno enačbo v delnih derivatih, katerih rešitve opisujejo atom vodika. Ali so valovne funkcije ψ omenjene na začetku.

Ta diferencialna enačba vključuje tri prostorske koordinate plus čas, toda ko ni vključena, je rešitev Schrödingerjeve enačbe analogna solostnim valom (val, ki se širi med določenimi mejami).

Valovne funkcije

Schrödingerjeva neodvisna časovna enačba je rešena v sferičnih koordinatah in rešitev je zapisana kot produkt treh funkcij, po eno za vsako prostorsko spremenljivko. V tem koordinatnem sistemu namesto uporabe koordinat kartezijanskih osi x, in in z Uporabljajo se koordinate r, θ in φ. Na ta način:

Vam lahko služi: vzporedno vezje

ψ (r, θ, φ) = r (r) ⋅F (θ) ⋅G (φ)

Funkcija valov je nematerialna, kljub kvantni mehaniki nam pove, da je kvadratna amplituda:

| ψ (r, θ, φ) |²

To pomeni, da je modul ali absolutna vrednost valovne funkcije, kvadratna r, θ in φ.

In to dejstvo je nekaj bolj konkretnega in oprijemljivega.

Če želite najti valovno funkcijo, morate rešiti tri navadne diferencialne enačbe, po eno za vsako spremenljivko r, θ in φ.

Rešitve vsake enačbe, ki bodo funkcije r (r), f (θ) in g (φ), vsebujejo prve tri kvantne številke.

Kakšne so kvantne številke?

Spodaj na kratko opišemo naravo vsake kvantne številke. Prvi trije, kot je navedeno zgoraj, izhajajo iz rešitev Schrödingerjeve enačbe.

Četrto številko je leta 1928 dodal Paul Dirac (1902 - 1984).

Glavna kvantna številka

Označuje ga n in označuje velikost dovoljene orbitale, pa tudi energijo elektrona. Višja kot je njegova vrednost, bolj je elektron jedra in tudi njena energija bo, vendar v zameno zmanjšuje svojo stabilnost.

Ta številka izhaja iz R (r) funkcije, ki je verjetnost, da bo elektron našel na določeni razdalji r jedra, ki ga določa:

 Kjer sodelujejo naslednje konstante:

-Planck Constant: H = 6.626 × 10 ^{-3. 4} J.s
-Elektronska masa m_in = 9.1 × 10^-31 kg
-Obremenitev elektronov: E = 1.6 × 10^-19 C.
-Elektrostatična konstanta: K = 9 × 10 ⁹ N.m²/C²

Ko n = 1 ustreza polmeru Bohr, ki je vreden približno 5.3 × 10⁻¹¹ m.

Razen prve plasti so ostali razdeljeni na podpredsednice ali pod -ravni. Vsak plast ima energijo v volt elektronu, ki jo daje:

Vam lahko služi: mehanski valovi: značilnosti, lastnosti, formule, vrste

Izraz EV "Electron Volt" pomeni, enota energije, ki se pogosto uporablja na območju kvantne fizike. Kjer je n = 1, 2, 3, 4 .. . in vsaka n vrednost ustreza a plast, To je označeno z velikimi črkami:

• K (n = 1)
• L (n = 2)
• M (n = 3)
• N (n = 4)
• Ali (n = 5)
• P (n = 6)
• Q (n = 7).

Teoretično ni zgornje meje za n, v praksi pa opazimo, da doseže le n = 8. Najmanj možna energija ustreza n = 1 in je energija Temeljna država.

Azimutalna kvantna številka ali kotni zagon

Ta številka, označena s poševno črko, določa obliko orbitalov, ko količinsko določi velikost orbitalnega kotnega zagona elektrona.

Na primer lahko vzamete celotne in pozitivne vrednosti med 0 in N-1:

-Ko je n = 1, potem ℓ = 0 in obstaja en sam pod -ravni.

-Če je n = 2, potem je ℓ lahko vreden 0 ali 1, tako da imate dve pod -lovki.

-In če je n = 3, potem ℓ prevzame vrednosti 0, 1 in 2 in obstajajo 3 pod -ravni.

Sledi ga lahko v nedogled, čeprav kot že rečeno, v praksi N doseže do 8. Pod -ravni so označene s črkami: s, str, d, F in g In naraščajo v energiji.

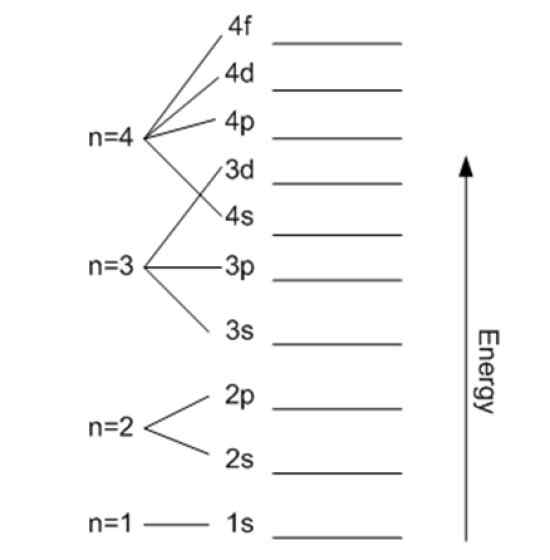Energija je povezana z glavnim kvantnim številom. Vir: Wikimedia Commons.

Magnetna kvantna številka m_ℓ

Ta številka odloča o orientaciji orbitala v prostoru in njena vrednost je odvisna od ℓ.

Za dani ℓ obstajajo (2ℓ+1) celotne vrednosti m _ℓ, ustreza ustreznim orbitalom. To so:

-ℓ, ( - ℓ+1),… 0,… (+ℓ -1),+ℓ.

Primer

Če je n = 2, vemo, da je ℓ = 0 in ℓ = 1, potem m _ℓ Vzemite naslednje vrednosti:

-Za ℓ = 0: m _ℓ = 0.
-Za ℓ = 1: m _ℓ = -1, m _ℓ = 0, m _ℓ = +1

Orbital n = 2 ima dve pod -ravni, prvi z n = 2, ℓ = 0 in m _ℓ = 0. Potem imamo drugo pod -levo: n = 2, ℓ = 1, s 3 orbitali:

• N = 2, ℓ = 1, m _ℓ = -1
• N = 2, ℓ = 1, m _ℓ = 0
• N = 2, ℓ = 1, m _ℓ = +1

Tri orbitale imajo enako energijo, vendar drugačno prostorsko usmerjenost.

Kvantno število spin m_s

Pri reševanju Schrödingerjeve enačbe v treh dimenzijah se pojavijo že opisane številke. Vendar v vodiku opazimo še nadaljnjo strukturo, kot pa te številke ni dovolj za razlago.

Lahko vam služi: konstanta gaze: kaj je, izračun in primeri

Zato je leta 1921 Wolfgang Pauli predlagal obstoj četrte številke: Število št_s, ki zahteva vrednosti +½ ali -½.

S to številko je opisana zelo pomembna lastnost elektrona, ki je prepir, Beseda, ki izvira iz angleščine prepir (obrnite se). In vrtenje je povezano z magnetnimi lastnostmi atoma.

Eden od načinov za razumevanje spina je, da si predstavljate, da se elektron obnaša kot majhen magnetni dipol (magnet s severnim in južnim polom), zahvaljujoč vrtenju okoli lastne osi. Obrat je lahko v isti smeri kot igle ure ali v nasprotni smeri.

Čeprav je Pauli predlagal obstoj te številke, so rezultati poskusa, ki sta ga izvedla Otto Stern in Walter Gerlach leta 1922, že pričakovali.

Tem znanstvenikom je uspelo razdeliti žarek srebrnih atomov z uporabo ne -uniformnega magnetnega polja.

Vrednost m_s Ni odvisno od n, ℓ in m _ℓ. Grafično ga predstavlja puščica: puščica navzgor označuje urnik in ena navzdol protihoran.

Načelo izključitve Paulija

Obnašanje elektronov v atomu je povzeto v načelu izključitve Paulija, ki navaja, da dva elektrona atoma ne moreta obstajati v istem kvantnem stanju.

Zato mora imeti vsak elektron drugačen nabor kvantnih števil n, ℓ, m _ℓ in m_s.

Pomen kvantnih števil in to načelo je v razumevanju lastnosti elementov v periodični tabeli: elektroni so organizirani v plasteh po N, nato.

Reference

1. Alonso, m. 1971. Kvantni in statistični temelji. Interameriški izobraževalni sklad.
2. Bauer, w. 2011. Fizika za inženiring in znanosti. Zvezek 1. MC Graw Hill.
3. Chang, R. 2013. Kemija. 11VA. Izdaja. MC Graw Hill Education.
4. Eisberg-Resnick. 1989. Kvantna fizika. Limusa - Wiley.
5. Giambattista, a. 2010. Fizika. 2. mesto. Ed. McGraw Hill.
6. Rex, a. 2011. Osnove fizike. Pearson.
7. Tippens, str. 2011. Fizika: pojmi in aplikacije. 7. izdaja. McGraw Hill.