Značilnosti, vrste in primeri pravokotnega gibanja

On rektno gibanje To je tisto, v katerem se mobilni telefon premika po ravni črti in zato prehaja v dimenzijo, zato prejme tudi ime Enodimenzionalno gibanje. Ta ravna črta je usmeritev ali pot, ki ji sledi predmet, ki se premika. Avtomobili, ki potujejo po aveniji slike 1, sledijo tej vrsti gibanja.

To je najpreprostejši model gibanja, ki si ga je mogoče zamisliti. Vsakodnevna gibanja ljudi, živali in stvari pogosto kombinirajo prenose v ravni črti z gibi vzdolž krivulj, nekateri.

Slika 1. Avtomobili, ki se premikajo po pravokotni aveniji. Vir: Pixabay.

Tu je nekaj dobrih primerov:

- Ko tečete po 200 -metrskem pravokotnem tiru.

- Vožnja z avtomobilom na ravni cesti.

- Prosto spuščanje predmeta z določene višine.

- Ko se žoga vrže navpično.

https: // giphy.com/gifs/j5xx3Bynaqv06wtoxq

Zdaj je cilj opisovanja gibanja dosežen z določitvijo značilnosti, kot so:

- Položaj

- Premik

- Hitrost

- Pospešek

- Čas.

Da bi opazovalec zaznal gibanje predmeta, je treba imeti referenčno točko (izvor O) in vzpostaviti določen naslov x, os in ali katero koli drugo.

Kar zadeva predmet, ki se premika, ima to lahko nešteto načinov. V zvezi s tem ni omejitev, vendar bo v vsem, kar sledi, domnevali, da je mobilni del delček; predmet tako majhen, da njene dimenzije niso pomembne.

Znano je, da to ne velja za makroskopske predmete; Vendar je model z dobrimi rezultati v opisu globalnega gibanja predmeta. Na ta način je lahko delček avtomobil, planet, oseba ali kateri koli drug predmet, ki se premika.

Začeli bomo s študijem pravokotne kinematike s splošnim pristopom k gibanju, nato pa bomo preučevali določene primere, kot so že imenovani.

[TOC]

Splošne značilnosti pravokotnega gibanja

Naslednji opis je splošen in uporaben za katero koli vrsto enega -dimenzionalnega gibanja. Prva stvar je izbrati referenčni sistem. Črta, vzdolž katere poteka gibanje, bo os x. Parametri gibanja:

Položaj

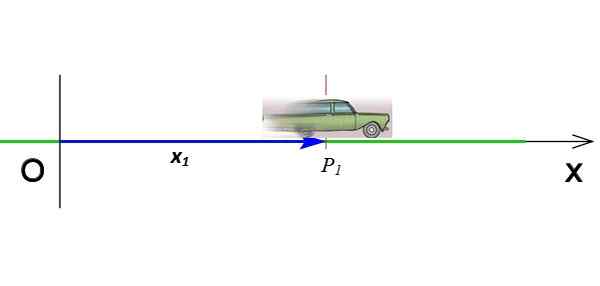Slika 2. Položaj mobilnega telefona, ki se premika na osi x. Vir: Wikimedia Commons (Modified by F. Zapata).

Je vektor, ki sega od izvora do točke, ko je predmet v trenutku. Na sliki 2 vektor x₁ Označuje položaj mobilnega telefona, ko je v koordinatu Str₁ in v času t₁. Pozicijske vektorske enote v mednarodnem sistemu so metri.

Premik

Premik je vektor, ki označuje spremembo položaja. Na sliki 3 je avtomobil prešel s položaja Str₁ v položaj Str₂, Zato je njegov premik δx = x₂ - x₁. Premik je odštevanje dveh vektorjev, simbolizira se z grško črko δ ("delta") in je vektor. Njegove enote v mednarodnem sistemu so metri.

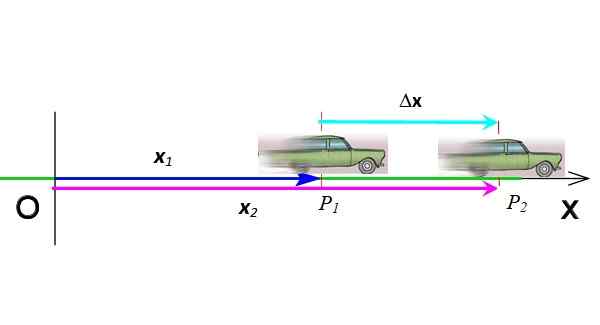Slika 3. Vektorski premik. Vir: Pripravil F. Zapata.

Vektorji so označeni s krepko v tiskanem besedilu. Toda če ste na isti dimenziji, lahko po želji storite brez vektorja.

Vam lahko služi: veje klasične in sodobne fizike

Prevožena razdalja

Razdalja d Obiščen s premikajočim se objektom je absolutna vrednost vektorja premika:

D = ΙxΙ = δx

Ker je absolutna vrednost, je prevožena razdalja vedno večja ali enaka 0, njegove enote pa so enake tistim v položaju in premiku. Absolutna zapis vrednosti je mogoče storiti z modulskimi vrsticami ali preprosto odstraniti krepko črko v tiskanem besedilu.

Povprečna hitrost

Kako hitro se položaj spreminja? Obstajajo počasni in hitri mobilni telefoni. Ključ je bila vedno hitrost. Za analizo tega faktorja se položaj analizira x funkcija časa t.

Povprečna hitrost v_m (Glej sliko 4) Je naklon sušilne črte (fuchsia) na krivuljo x VS t in ponuja globalne informacije o mobilnem premiku v obravnavanem časovnem intervalu.

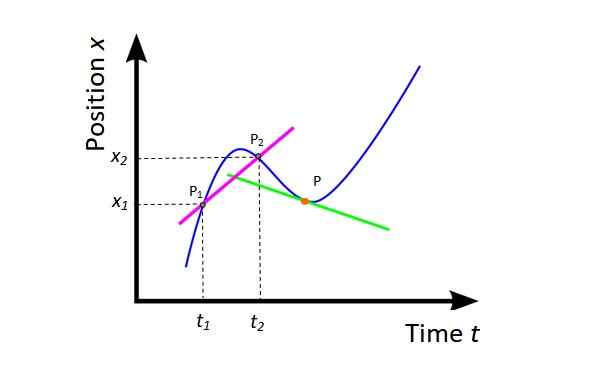Slika 4. Povprečna hitrost in trenutna hitrost. Vir: Wikimedia Commons, spremenjena s. Zapata.

v_m = (x₂ - x₁) / (t₂ -t₁) = Δx / Δt

Povprečna hitrost je vektor, katerega enote v mednarodnem sistemu so metri /sekundo (gospa).

Trenutna hitrost

Povprečna hitrost se izračuna tako, da vzamemo merljiv časovni interval, vendar ne obvešča o tem, kaj se zgodi v omenjenem intervalu. Če želite vedeti hitrost, morate časovni interval narediti zelo majhen, matematično je enakovreden:

ΔT → 0

Enačba je prej dana za povprečno hitrost. Na ta način dobimo takojšnjo hitrost ali preprosto hitrost:

Geometrijsko je derivat položaja glede na čas naklon črte tangenta do krivulje x VS t na določeni točki. Na sliki 4 je točka oranžna in tangentna črta je zelena. Trenutna hitrost na tej točki je naklon te črte.

Hitrost

Hitrost je opredeljena kot modul absolutne vrednosti ali hitrosti in je vedno pozitiven (signalizacija, ceste in avtoceste so vedno pozitivni, nikoli negativni). Izraza "hitrost" in "hitrost" se lahko uporabljata vsak dan, v fiziki pa je potrebno razlikovanje med vektorjem in plezanjem.

v = ΙvΙ = v

Povprečni pospešek in takojšen pospešek

Hitrost se lahko med gibanjem spremeni in resničnost je, da se pričakuje, da bo to storila. Obstaja velikost, ki to spremembo količinsko opredeli: pospešek. Če opazimo, da je hitrost sprememba položaja glede na čas, je pospešek sprememba hitrosti glede na čas.

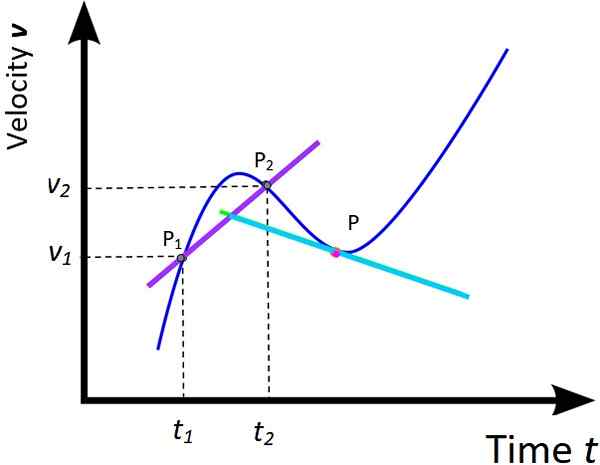Slika 5. Povprečni pospešek in takojšen pospešek. Vir: Wikimedia Commons, spremenjena s. Zapata.

Obdelava, ki je bila dana graf x VS t od obeh prejšnjih razdelkov je mogoče razširiti na ustrezen graf v VS t. Posledično sta povprečna pospešek in takojšen pospešek opredeljena kot:

do_m = (v₂ - v₁) / (t₂ -t₁) = Δv / Δt  (Do bivališča)

Pospešek in pojem

V enem dimenzionalnem gibanju imajo vektorji s konvencijo pozitivne ali negativne znake, saj gredo tako ali drugače. Ko ima pospešek enak pomen kot hitrost, poveča njegovo velikost, ko pa ima nasprotno smiselno in hitrost zmanjša svojo velikost. Nato se reče, da se gibanje zavleče.

Vam lahko služi: leyden steklenica: deli, delovanje, poskusi

Fantje

Klasifikacija pravokotnih gibov se običajno izvaja na podlagi:

- Ali je pospešek konstanten ali ne.

- Gibanje prehaja po vodoravni ali navpični črti.

Gibanje s stalnim pospeševanjem

https: // giphy.com/gifs/ylzfnbidhm7rp391fi

Ko je pospešek konstanten, povprečni pospešek do_m Je enak takojšnjemu pospeševanju do In obstajata dve možnosti:

- Da je pospešek vreden 0, v tem primeru je hitrost konstantna in ima enakomerno pravokotno gibanje ali MRU.

- Stalni pospešek, ki se razlikuje od 0, v katerem hitrost raste ali se sčasoma linearno zmanjšuje (pravokotno gibanje enakomerno raznoliko ali MRUV):

Kje v_F  in t_F So končna hitrost in čas in v_tudi in t_tudi So začetna hitrost in čas. Ja t_tudi = 0, Pri čiščenju končne hitrosti imate enačbo že znane za končno hitrost:

v_F = v_tudi + Ob

Za to gibanje veljajo tudi naslednje enačbe:

- Položaj, odvisno od časa: x = x_tudi + v_{tudi .}T +½ at²

- Hitrost, odvisno od položaja: v_F² = v_tudi² + 2. mesto.Δx  (Z δx = x - x_tudi)

Vodoravna gibanja in navpični gibi

Vodoravni gibi so tisti, ki prehajajo po vodoravni osi ali osi x, medtem ko navpični to počnejo vzdolž osi in osi. Vertikalna gibanja pod delovanjem gravitacije so najpogostejša in zanimiva.

V prejšnjih enačbah je vzeta A = g = 9.8 m/s² usmerjena navpično navzdol, smer, ki je skoraj vedno izbrana z negativnim znakom.

Na ta način, v_F = v_tudi + Ob Se preoblikuje v_F = v_tudi - Gt In če je začetna hitrost 0, ker je bil predmet prosto spuščen, je še dodatno poenostavljen na v_F = - gt. Dokler se zračni odpor ne upošteva, seveda.

Rešeni primeri

Primer 1

V točki se sprosti majhen paket, tako da se premika po transporterju z drsnimi kolesi ABCD, prikazano na sliki. Medtem ko se spuščajo skozi nagnjene odseke AB in CD, paket nosi pospeševanje 4,8 m/s², Medtem ko v vodoravnem delu BC ohranja konstantno hitrost.

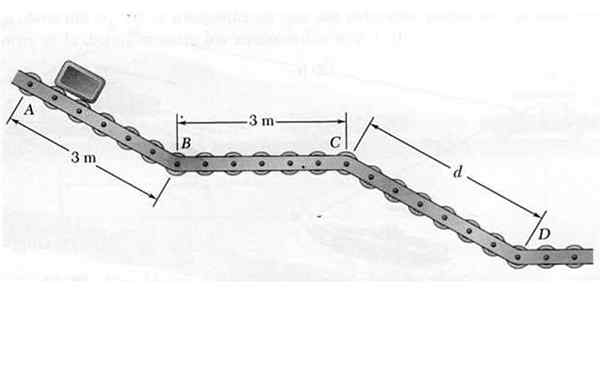Slika 6. Paket, ki se premika po drsni poti rešenega primera 1. Vir: Self Made.

Če veste, da je hitrost, s katero je paket pri D doseženo, 7,2 m/s, določite:

a) Razdalja med C in D.

b) Čas, potreben za končni paket.

Rešitev

Premik paketa se izvede v treh prikazanih rekvilinearnih odsekih in za izračun zahtevanih hitrosti je potrebna hitrost v točkah B, C in D. Analizijmo vsak razdelek ločeno:

Oddelek AB

Ker čas v tem razdelku ni na voljo, bo uporabljen v_F² = v_tudi² + 2. mesto.Δx  Z vo = 0:

v_F² = 2a.Δx → v_F²= 2. 4,8 m/s² . 3 m = 28.8 m²/s² → v_F  = 5.37 m/s = v_B

Čas, ki ga potrebuje paket za potovanje v odsek AB, je:

t_Ab = (v_F - v_tudi) /A = 5.37 m/s/4,8 m/s² = 1.19 s

Oddelek BC

Hitrost v odseku BC je torej konstantna v_B = v_C = 5.37 m/s. Čas, ki je potreben za potovanje v ta razdelek, je:

Vam lahko služi: Light Refrection: Elementi, zakoni in eksperimentiranje

t_Pr = razdalja _Pr  / v_B = 3 m/ 5.37 m/s = 0.56 s

Oddelek CD

Začetna hitrost tega razdelka je v_C = 5.37 m/s, Končna hitrost je v_D = 7,2 m/s, prek v_D²  = v_C² + 2. do. d Vrednost d:

D = (v_D²  - v_C²)/2.a = (7.2²  - 5.37²)/2 x 4.8 m = 2.4 m

Čas se izračuna kot:

t_{CD =} (v_D  - v_C)/A = (7.2- 5.37)/ 4.8 s = 0.38 s.

Odgovori na postavljena vprašanja so:

a) d = 2.4 m

b) Čas potovanja je t_Ab + t_Pr + t_CD = 1.19 S +0.56 S +0.38 S = 2.13 s.

Primer 2

Oseba je pod vodoravnimi vrati, ki je sprva odprta in visoka 12 m. Oseba navpično sproži predmet proti vrati.

Znano je, da se vrata zaprejo 1,5 sekunde po tem, ko je oseba objekt sprožila z višine 2 metra. Zračni odpor ne bo upoštevan. Odgovorite na naslednja vprašanja in opravičite:

a) Ali vam uspe prenesti predmet skozi vrata, preden se zapre?

b) Ali se bo predmet kdaj trčil ob zaprta vrata? Če je pritrdilno, kdaj se to zgodi?

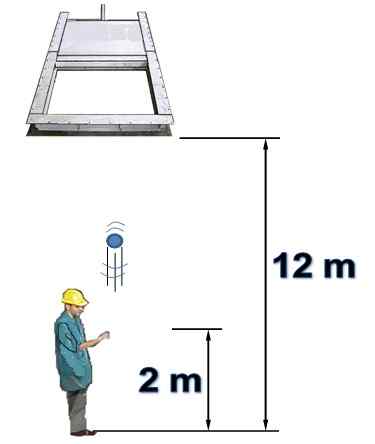Slika 7. Predmet se zažene navpično navzgor (Rešen primer 2). Vir: Self Made.

Odgovor na)

Med začetnim položajem žoge in vrat je 10 metrov. To je navpična lansiranje, v katerem je ta naslov jet kot pozitiven.

Hitrost, ki jo ima, lahko ugotovite, ko pridete do te točke, s tem rezultatom, ko bi potrebovali, da to storite, in jo primerjati s časom zapiranja vrat, ki je 1.5 sekund:

v_F ²= v_tudi ²- 2.g. Δin → v_F = (15² - 2 x 9.8 x10)^1/2 M = 5.39 m/s

T = (v_F - v_tudi) /g = (5.39 - 15) / (-9.8) S = 0.98 s

Ker je ta čas manj kot 1.5 sekund, potem je sklenjeno, da lahko predmet vsaj enkrat skozi vrata.

Odgovor B)

Že vemo, da predmet upravlja. Hitrost, ko sega na višini vrat, ima enako velikost kot takrat, ko gre navzgor, vendar v nasprotni smeri. Zato delajte z -5.39 m/s in čas, ki je potreben za dosego te situacije, je:

T = (v_F - v_tudi) /G = (-5.39 - 15) / (-9.8) S = 2.08 s

Ker vrata ostanejo odprta le za 1.5 s, očitno je, da nima časa, da bi prešel, preden se zapre, saj se mu zdi, da je zaprta. Odgovor je: predmet, če se po 2 trči v zaprta vrata.08 sekund po izpustu, ko pride v spust.

Reference

1. Figueroa, d. (2005). Serija: Fizika za znanost in inženiring. Zvezek 1. Kinematika. Uredil Douglas Figueroa (USB).69-116.
2. Giancoli, d. Fizika. (2006). Načela z aplikacijami. 6^th Izdaja. Dvorana Prentice. 22-25.
3. Kirkpatrick, l. 2007. Fizika: pogled na svet. 6^ta Skrajšana izdaja. Cengage učenje. 23 - 27.
4. Resnick, r. (1999). Fizično. Zvezek 1. Tretja izdaja v španščini. Mehika. Continental uredništvo s.Do. od c.V. 21-22.
5. Rex, a. (2011). Osnove fizike. Pearson. 33 - 36
6. Sears, Zemansky. 2016. Univerzitetna fizika s sodobno fiziko. 14^th. Ed. Zvezek 1. 50 - 53.
7. Serway, r., Jewett, J. (2008). Fizika za znanost in inženiring. Zvezek 1. 7^ma. Izdaja. Mehika. Uredniki učenja Cengage. 23-25.
8. Serway, r., Vulle, c. (2011). Osnove fizike. 9^na Ed. Cengage učenje. 43 - 55.
9. Wilson, J. (2011). Fizika 10. Pearson Education. 133 - 149.