Fizično

Nihalo gibanje

Nihalo gibanje

Kaj je nihalo gibanje?

On nihalo gibanje Gre za nihajno gibanje, ki ga je naredil bolj ali manj težak predmet, imenovan nihalo, suspendirano s svetlobo ali palico, pritrjeno na drugem koncu.

Nihalo je podeljeno začetni impulz in je dovoljeno nihaj. To je načelo delovanja nihajnih ur, gugalnic, zibanja stolov in Metronomi nihala, ki se uporablja za označevanje časov v glasbi.

Nihanje nihanja, ki prikazuje hitrost in pospeševanje (Wikipedia.org)

Govori se, da je Galileo Galilei do leta 1581 opazoval visek svetilke v Pisini katedrali in opazil, da se je, čeprav se amplituda nihanja svečnikov zmanjšuje zaradi trenja z zrakom, ne pa trajanja trajanja trajanja trajanja cikla.

To je pritegnilo pozornost Galileoja, ki se je odločil nadaljevati s študijo, in ugotovil, da obdobje nihala ni odvisno od testa, ampak od kvadratnega korena dolžine vrvi, kot bo razvidno pozneje.

Značilnosti nihala

Nihalo je zelo enostavno graditi, saj je dovolj z visenjem bombažne niti in ga na drugem koncu drži s prsti ali ga privežete na podporo kot noht.

Po majhnem začetnem impulzu je teža odgovorna za ohranjanje nihanja nihanja, čeprav trenje zmanjšuje amplitudo gibanja, dokler končno ne preneha.

Glavna značilnost nihala je, da se ponavlja, saj gre za gibanje. Zdaj je za olajšanje študije priročno narediti nekaj poenostavitve, da se osredotočite na enostavnejši model, imenovan Preprosto nihalo.

Preprosto nihalo

Otroka v zamahu je mogoče modelirati kot preprosto nihalo

To je idealen sistem, ki ga sestavljajo vod, ki velja za točno maso m, ob upoštevanju svetlobne in neiztežljive vrvi dolžine L. Značilnosti tega sistema so:

  • Imajo ponavljajoče se in periodično gibanje, sestavljeno iz tega, da se vračate naprej in nazaj lok oboda polmera, ki je enak L.
  • Ne upošteva trenja.
  • Amplituda gibanja je majhna (< 5º).
  • Obdobje je neodvisno od mase m, In odvisno je izključno na dolžini L nihala.
Vam lahko služi: rezultat vektorja: izračun, primeri, vaje

Formule in enačbe

Sledi preprost nihalni diagram, na katerem delujeta dve sili: teža Str velikosti Mg, ki je usmerjena navpično navzdol in napetost T Na vrvi. Ne veljajo za trenje.

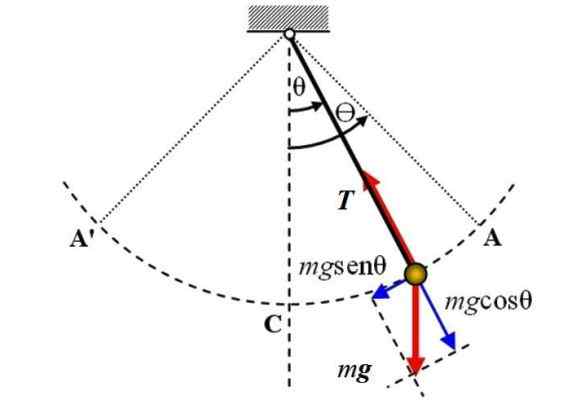Brezplačni karoserijski diagram preprostega nihala. Vir: Wikimedia Commons.

Referenčna os je navpična os in sovpada s položajem θ = 0, od tam se meri kotni premik θ, bodisi v eno ali drugo smer. Znak + lahko na sliki dodelite desno.

Za preučevanje nihalnega gibanja je izbran koordinatni sistem z izvorom v samem nihalu. Ta sistem ima tangencialno koordinato na obod A'CA, ki ga opisuje nihalo, kot tudi radialna koordinata.

V trenutku, prikazanem na sliki, se nihalo premika v desno, vendar tangencialna komponenta gravitacije, imenovana Ft, je odgovoren za vrnitev. Na številko je opozorjeno, da ima ta komponenta smiselno v nasprotju z gibanjem.

Kar zadeva napetost na vrvi, je uravnotežen s komponento teže mgcosθ.

Neto sila je torej tista, imenovana Ft In po Newtonovem drugem zakonu je enak izdelku Masa × Pospešek, In to je drugo, ki izhaja iz linearnega premika s, Kaj je lok, ki ga prehodi nihalo. Tako:

Kotni premik 

Enačba mora biti izražena v smislu ene same spremenljivke, pri čemer se spomnimo, da sta kotni premik θ in prevoženi lok povezan z enačbo:

Lahko vam služi: drugi zakon termodinamike: formule, enačbe, primeri

s = l.θ

Masa se prekliče na obeh straneh in če je amplituda majhna, tudi kot θ, na nek način velja naslednji pristop:

sin θ ≈ θ

S tem dobimo naslednjo diferencialno enačbo za spremenljivko θ (t):


To enačbo je zelo enostavno rešiti, saj je njegova rešitev funkcija, katere drugi izpeljan je sama funkcija. Obstajajo tri alternative: kosinus, ena dojka ali eksponentna. Kosinusna funkcija je izbrana za kotni premik θ (t), saj je dobro znana in enostavna za ravnanje z ravnanjem.

Bralec lahko dvakrat preveri, da naslednja funkcija izpolnjuje diferencialno enačbo:

θ (t) = θm cos (ωt + φ)

Kjer θm Najdaljši kot je nihalo premikal glede na navpično in kotno frekvenco ω::

Konstanta φ se doda, da se rešilni rešili in se prilega v skladu z začetnimi pogoji.

Enačba obdobja

T -obdobje gibanja je čas, potreben za izvedbo cikla in je opredeljen kot:

Zamenjava ω:

Kot je bilo že ugotovljeno, obdobje ni odvisno od mase nihala, ampak le od njegove dolžine.

Primeri nihalnega gibanja

Ukrep srčnega utripa

Galileo je imel pojav merjenja srčnega utripa ljudi, prilagajal je dolžino nihala, dokler se obdobje s pulzacijami srca sovpada.

Ura nihala

To je nedvomno eden najbolj znanih primerov nihala. Izdelava nihajnih ur ima tako znanost kot umetnost. Nizozemski fizik Christian Huygens (1629-1695) je leta 1656 razvil prvo nihalo na podlagi študije, ki jo je pred leti naredila Galileo.

Vam lahko služi: valovita optika

Foucaultov nihalo

Foucault nihalo. Vir: Wikimedia Commons.

Je nekoliko drugačno nihalo, kot je opisano zgoraj, saj se lahko obrne v kateri koli navpični ravnini. Ustvaril ga je francoski fizik Léon Foucault (1819-1868) in se uporablja za vizualizacijo vrtenja zemlje.

Vaja rešena

Preprosto nihalo mine vsakih 0.5 s za ravnotežni položaj. Kakšna je dolžina niti?

Rešitev

Ker je obdobje potreben čas za celoten cikel, v katerem dvakrat preide skozi ravnotežni položaj: eno najprej in drugo nazaj, nato pa:

T = 2 × 0.5 s = 1 s

Od:

Dolžina l niti je očiščena:

Nit meri 0.25 m ali 25 cm dolg.

Reference

  1. Figueroa, d. (2005). Serija: Fizika za znanost in inženiring. Zvezek 2. Dinamično. Uredil Douglas Figueroa (USB).
  2. Giambattista, a. 2010. Fizika. 2. mesto. Ed. McGraw Hill.
  3. Giancoli, d.  2006. Fizika: načela z aplikacijami. 6. Ed Prentice Hall.
  4. Katz, d. 2013. Fizika za znanstvenike in inženirje. Temelje in povezave. Cengage učenje.
  5. Vitez, r.  2017. Fizika za znanstvenike in inženiring: strateški pristop.  Pearson.