Blokirajte elemente algebre, primeri, rešene vaje

On Blok algebra Se nanaša na nabor operacij, ki se izvajajo prek blokov. Ti in nekateri več elementov služijo shematično predstavljanju sistema in enostavno vizualizirati vaš odziv na določen vnos.

Na splošno sistem vsebuje različne električne, elektronske in elektromehanske elemente, vsak od njih pa je s svojo funkcijo in položajem v sistemu ter načinom, kako sta povezana, shematizirana skozi funkcionalne bloke.

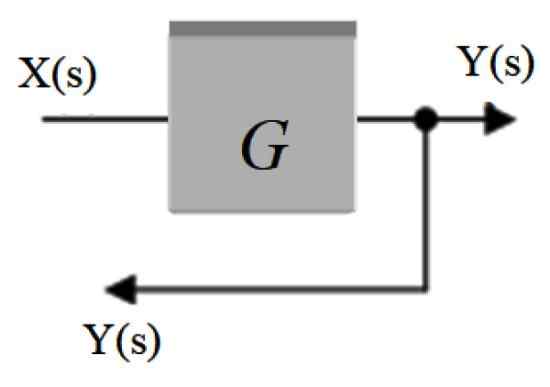
Slika 1.

Na zgornji sliki je zelo preprost sistem, ki je sestavljen iz vhodnega signala x (s), ki vstopi v blok s funkcijo prenosa G (s), ki ga spreminja in proizvaja izhod y (s).

Priročno je predstavljati signale in njihovo potovanje skozi sistem skozi puščice, ki vstopijo in zapustijo vsak blok. Običajno je tok signala usmerjen od leve proti desni.

Prednost tovrstne sheme je vizualna pomoč, ki jo nudi za razumevanje sistema, čeprav ne pomeni fizične predstavitve istega. Pravzaprav blok diagram ni edinstven, saj lahko glede na stališče lahko narišemo celo več diagramov istega sistema.

Prav tako se lahko zgodi, da se isti diagram uporablja za več sistemov, ki niso nujno povezani med seboj, pod pogojem, da njegovo vedenje pravilno opisuje. Obstajajo različni sistemi, katerih odziv je v mnogih vidikih podoben, na primer LC vezje (induktor-kanal) in sistem za množično resort.

[TOC]

Kaj je blok diagram?

Sistemi so ponavadi bolj zapleteni kot na sliki 1, vendar blok algebra ponuja vrsto preprostih pravil za manipulacijo s sistemsko shemo in zmanjšanje na najpreprostejšo različico.

Kot je razloženo na začetku, diagram uporablja bloke, puščice in kroge, da vzpostavi razmerje med vsako komponento sistema in pretokom signalov, ki potekajo skozi njega.

Blok algebra omogoča primerjavo dveh ali več signalov z vsoto, odštevanjem in množenjem le -teh ter analizirati prispevek, ki ga vsaka komponenta prispeva k sistemu.

Zahvaljujoč temu je mogoče zmanjšati celoten sistem na en vhodni signal, edinstveno funkcijo prenosa, ki v celoti opisuje sistemsko dejanje in ustrezen izhod.

Lahko vam služi: Astroklimika: Zgodovina, kakšne študije, veje

Elementi blokovnega diagrama

Elementi blokovnega diagrama so naslednji:

Signal

Signali so zelo raznoliki, na primer, da je pogost, da je električni tok ali napetost, vendar je lahko svetel, zvok in še več. Pomembno je, da vsebuje informacije o določenem sistemu.

Signal je označen s kapitalsko črko, če je funkcija spremenljivke s Laplace Transform: x (s) (glej sliko 1) ali z malimi črkami, če temelji na času t, kot x (t).

V blok diagramu je vhodni signal predstavljen s puščico, usmerjeno proti bloku, medtem ko je izhodni signal, označen kot y (s) ali (t), označen z odhodno puščico.

Tako vhodni kot izhodni signal sta edinstven, naslov, v katerem informacije tečejo, je določeno s smerjo puščice. In algebra je enaka za katero koli od obeh spremenljivk.

Blok

Blok je predstavljen s kvadratom ali pravokotnikom (glej sliko 1) in ga je mogoče uporabiti za izvajanje operacij ali izvajanje funkcije prenosa, ki je običajno označena s kapitalsko črko G. Ta funkcija je matematični model, s katerim je opisan odziv, ki ga ponuja sistem.

Funkcijo prenosa se lahko izrazi glede na čas t na primer g (t) ali spremenljivka s kot g (s).

Ko vhodni signal X (S) prispe v blok, se pomnoži s funkcijo prenosa in se pretvori v izhodni signal y (s). Matematično je izraženo na naslednji način:

In (s) = x (s).G (s)

Prav tako je funkcija prenosa razmerje med Laplasovo transformacijo izhodnega signala in Laplaceom transformacijo vhodnega signala, pod pogojem, da so začetni pogoji sistema NULL:

G (s) = y (s) / x (s)

Vsota

Vsota ali poletje simbolizira krog s križem v notranjosti. Uporablja se za kombiniranje z vsotami in odštevanjem, dva ali več signalov. Na koncu puščice, ki simbolizira signal, se znak + postavi neposredno, če je dodan ta signal ali znak - če je odšteto.

Na naslednji sliki je primer, kako deluje poletje: imate vhodni signal X, h katerim se dodata signala A in B, ki dobivata kot rezultat izhoda in, ki je algebraično enak:

Vam lahko služi: navpični posnetek: formule, enačbe, primeri

Y = x+a+b

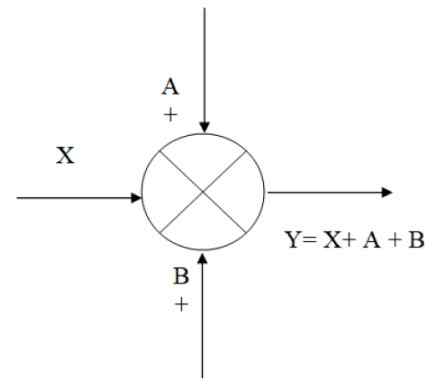Slika 2. Primer izvrševanja. Vir: f. Zapata.

Podružnična točka

Pokliče se tudi Točka bifurkacije. V njem se signal, ki izhaja iz bloka. Predstavljen je s točko, nameščeno na puščici signala, in iz nje prihaja druga puščica, ki signal preusmeri proti drugemu delu.

Slika 3. Podružnična točka. Vir: f. Zapata.

Primeri blokov algebre

Kot je bilo pojasnjeno že, je ideja izraziti sistem skozi blok diagram in ga zmanjšati, da bi našli funkcijo prenosa, ki ga opisuje. Sledijo pravila algebre blokov za poenostavitev diagramov:

Kaskadni bloki

Ko imate signal, ki zaporedno prehaja skozi G bloke₁, G₂, G₃..., zmanjša se na edinstven blok, katerega funkcija prenosa je produkt G₁, G₂, G₃..

V naslednjem primeru signal X (S) vstopi v prvi blok, njegov izhod pa je:

In₁(s) = x (s).G₁(S)

Slika 4. Dva bloka v slapu. Vir: f. Zapata.

Po vrsti in₁(s) Vnesite blok G₂(s), katerih odhod je:

In₂(s) = x (s).G₁(S). G₂(S)

Postopek velja za n kaskadne bloke:

In_n (s) = x (s). G₁(S).G₂(S) ... g_n(S)

Bloki vzporedno

V levem diagramu bifurca signala X (s) za vstop v bloke G₁(S) in g₂(S):

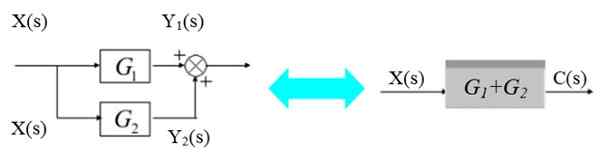Slika 5. Dva bloka vzporedno. Vir: f. Zapata.

Ustrezni izhodni signali so:

In₁(s) = x (s).G₁(S)

In₂(s) = x (s).G₂(S)

Ti signali se dodajo za pridobitev:

C (s) = y₁(s) +₂(s) = x (s).[G₁(s) + g₂(s)]

Kot je prikazano na desnem diagramu.

Premaknite zaveznika na levo

Poletje se lahko premakne na levo od bloka, kot sledi:

Slika 6. Premaknite dodatek na levi strani bloka. Vir: f. Zapata.

Na levi strani je izhodni signal:

C (s) = r (s). G (s) - x (s)

Enako desno:

C (s) = [r (s) - x (s)/g (s)]].G (s)

Premaknite desno v desno

Poletje se lahko tako premakne desno od bloka:

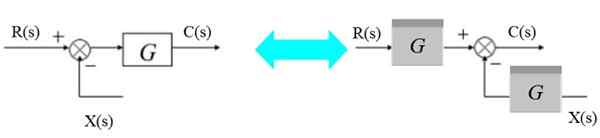Slika 7. Premaknite parcelo desno od bloka. Vir: f. Zapata.

Na levi strani imate: [r (s) - x (s)].G (s) = c (s)

Vam lahko služi: Načelo Archimedes: formula, demonstracije, aplikacije

In desno:

R (s). G (s) - x (s).G (s) = c (s)

Premaknite bifurkacijsko točko od leve proti desni

Če želite izpodriniti bifurkacijsko točko od leve proti desni strani bloka, je dovolj, da opazimo, da je izhod c (s) desno produkt x (s).G (s). Ker želite spet postati x (s), ga pomnoži inverzni g (s).

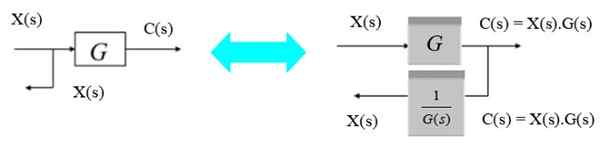Slika 8. Premaknite točko veje od leve proti desni. Vir: f. Zapata.

Premaknite bifurkacijsko točko od desne proti levi

Druga možnost je, da se bifurkacijska točka premika od desne proti levi, kot sledi:

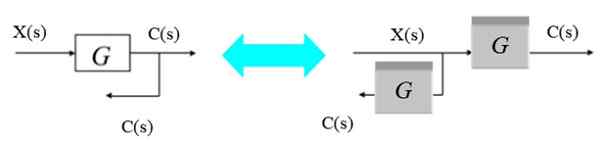Slika 9. Premaknite točko veje od desne proti levi. Vir: f. Zapata.

Ker želi izhod bifurkacije pridobiti C (S), je nov blok G (s) preprosto prepleten na bifurkacijski točki na levi strani prvotnega bloka.

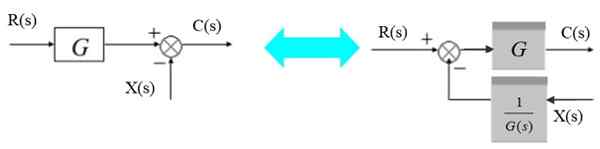
Sistem s povratnimi informacijami

V naslednjem sistemu se izhodni signal C (S) napaja skozi pokoreno na levi:

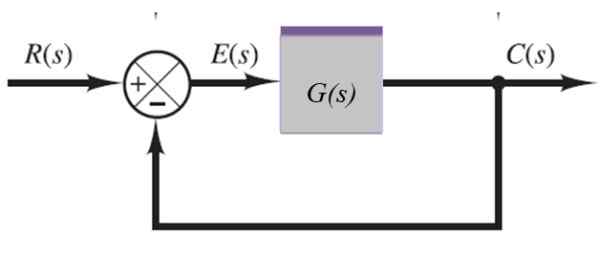Slika 10. Sistem s povratnimi informacijami. Vir: f. Zapata.

C (s) = e (s).G (s)

Toda:

E (s) = r (s) -c (s)

Nadomeščanje tega izraza v prejšnji enačbi je: c (s) = [r (s) -c (s)]].G (s), iz katerega je mogoče očistiti c (s):

C (s) + c (s).G (s) = r (s).G (s) → C (s). [1 + g (s)] = r (s).G (s)

C (s) = r (s).G (s) / [1 + g (s)]

Ali izmenično:

C (s) / r (s) = g (s) / [1 + g (s)]]

Grafično, po poenostavitvi je:

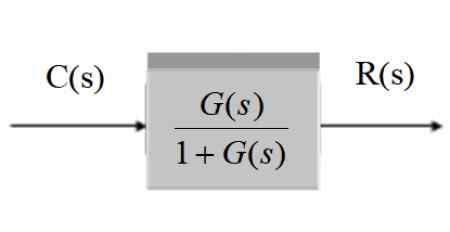Slika 11. Poenostavitev sistema s povratnimi informacijami. Vir: f. Zapata.

Sistem s povratnimi informacijami in pretvornikom

Transduktor je sestavljen iz funkcije prenosa h (S):

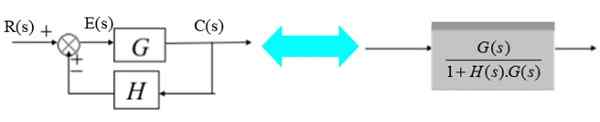Slika 12. Sistem s povratnimi informacijami in pretvornikom. Vir: f. Zapata.

Na desnem diagramu je izhodni signal c (s):

C (s) = e (s). G (s) z e (s) = r (s) - c (s).H (s)

Tako:

C (s) = [r (s) - c (s). H (s)]. G (s)

C (s) [1+ h (s).G (s)] = r (s).G (s)

Zato lahko C (s) očistimo::

C (s) = g (s).R (s) / [1+ h (s).G (s)]

In funkcija prenosa bo:

G (s) / [1+ h (s).G (s)]

Kot je prikazano v poenostavljenem desnem diagramu.

Rešene vaje

Vaja 1

Poiščite funkcijo prenosa naslednjega sistema:

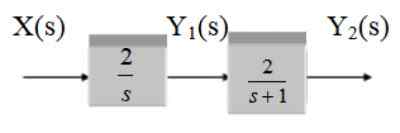Slika 13. Dva blokado v slapu. Vir: f. Zapata.

Rešitev

To je dva kaskadna bloka, zato je funkcija prenosa rezultat funkcij g₁ in g₂.

Moraš:

G₁ = 2/s

G₂ = 2 /(S+1)

Zato je iskana funkcija prenosa:

G (s) = 4 / [s (s+1)]

Vaja 2

Zmanjšajte naslednji sistem:

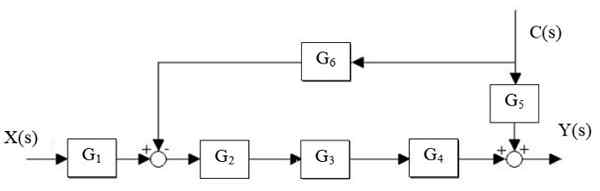Slika 14. Poenostavitev sistema. Vir: f. Zapata.

Rešitev

Najprej se zmanjša g kaskada₂, G₃ in g_4, In vzporedna g je ločena₅ in g₆:

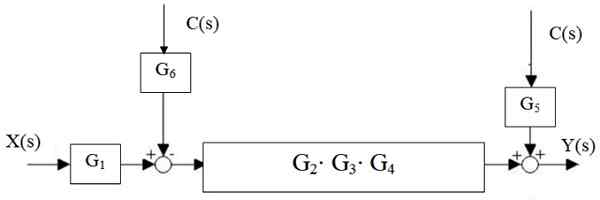Slika 15. Zmanjšanje osrednjega slapa. Vir: f. Zapata.

Nato je Suitor levo od bloka G₂ ⋅G₃ ⋅ g₄ Premakne se v desno:

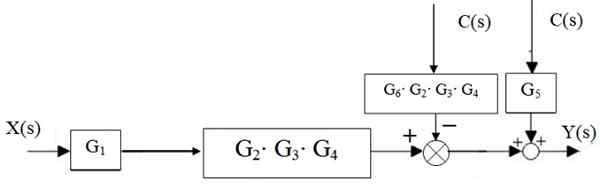Slika 16. Prenos amanicije. Vir: f. Zapata.

Summers desne so zmanjšana na eno, pa tudi kaskadne bloke:

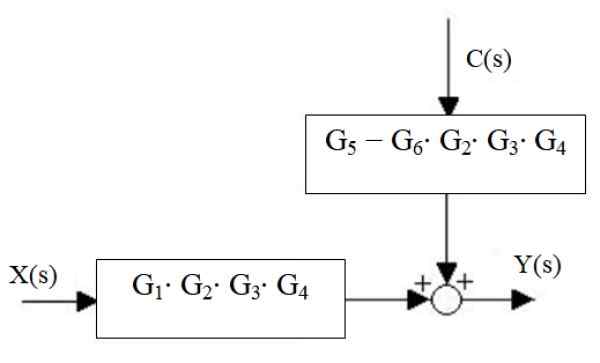Slika 17. Zmanjšanje novega slapa in poletja desnice. Vir: f. Zapata.

Končno je sistemski izhod:

In (s) = x (s) ⋅G₁⋅ g₂ ⋅G₃ ⋅ g₄ + C (s) ⋅ [g₅ - G₆ ⋅ g₂ ⋅G₃ ⋅ g₄]

Reference

1. Alaydi, j. Nadzor diagrama sistemskega bloka. Obnovi se od: spletnega mesta.iugaza.Edu.$.
2. Bolton, w. 2006. Kontrolni inženiring. 2. mesto. Izdaja. Alpha omega.
3. Cwalinsky, J. Uvod v algebro sistemskega bloka. Okrevano od: cedengineering.com.
4. DademuchConnection. Diagram blokov. Okreval od: Dademuch.com.
5. Ogata, k. 2010. Sodobni nadzorni inženiring. 5. Izdaja. Pearson.