Kemija

Zakon več razsežnosti

Zakon več razsežnosti

Kakšen je zakon več razsežnosti?

The Zakon več razsežnosti Ugotavlja, da če dva elementa tvorita več kot eno spojino, ko reagirata drug na drugega, potem je delež mase, s katerimi je ena od njih združena s fiksno maso drugega.

Izjava zakona se morda zdi zapletena, če nimate primera na roki. Zato razmislite o nekaterih piškotih Oreos, sestavljenih iz dveh čokoladnih pokrovov in traku sladke kreme: t2C (t = pokrov in c = krema). Če bi želeli izumiti močnejši piškotek Oreo, bi dodali še en trak smetane, da bi imeli dvojno smetano (t2C2 ali tc).

V sladicah, kot so piškotki Oreos, imamo deleže, ki jih je mogoče spreminjati preprosto za pripravo drugih različic. Vir: Brokensphere, CC BY-SA 3.0 https: // creativeCommons.Org/licence/by-sa/3.0 prek Wikimedia Commons

Lahko bi dodali še enega, tako da ima piškotek trikrat več smetane kot običajni piškotek (T2C3). Kaj pa, če postavimo še en čokoladni pokrov na sredino belih trakov (t3C2)? Možnosti so neomejene; Vedno pa dodamo pokrov ali smetana. Ne razmišljamo o polovici pokrova (1/2 T) ali petine smetane (1/5 C), ker bi bilo neprimerno.

Na enak način se zgodi s kemičnimi elementi: njihovi atomi se ne delijo po spojinah. Zato je množica T ali C med njihovimi spojinami "vedno" preprost odnos.

Pojasnilo

Delež

Zakon več razsežnosti, skupaj z zakonom določenih razsežnosti, je bil pred stohiometrijo in prvimi kemičnimi formulami. Pozabimo na piškotke, vendar ohranimo njihove simbole: t in c. Skozi poskuse je ugotovljeno, da elementi T in C tvorijo več spojin: t2C, tc in t2C3.

Pred kemičnimi formulami je bilo naenkrat nemogoče vedeti, katera so deleži mase T in C v takšnih spojinah. Naj bi jih najprej določil. V spojini je bilo ugotovljeno, da se je masa T podvojila na maso C; Če rečem, sta 2 grama t kombinirani z 1 gramom C.

Vam lahko služi: kapacitivnost: enote, formule, izračun, primeri

Nato se je v drugi spojini morala ujemati mase T in C: 2 grama t sta zdaj kombinirani z 2 grami C. Tu se postavlja vprašanje: Kaj pa, če lahko T in C še vedno tvorita drugo spojino? Če je tako, bi se zagotovo oblikovali z 2 grami T, tokrat pa bi jih združili s 3 grami C (1 gram + 1 gram + 1 gram).

Preprosti masni odnosi

Delež mase, s katerimi reakcija T in C omogočajo vzpostavitev njihovih kemičnih formul: T2C (2 grama T: 1 gram c), TC (2 grama t: 2 grama c) in t2C3 (2 grama T: 3 grama c). Če želimo primerjati razmerja med masami T ali C v teh spojinah, je potrebno, da ena od njegovih mas ostane konstantna; V tem primeru T: 2 grama.

Zato bomo v teh treh spojinah določili deleže mase C:

  • T2C: 1 gram c/2 grama t
  • TC: 2 grama c/2 grama t
  • T2C3: 3 grame c/2 grama t

Imeli bomo razmerje za maso C, enaka 1: 2: 3. To pomeni, da je v TC 2 -krat več C kot v t2C in še 3 -krat več c v t2C3 kot v t2C. Kot je razvidno, so 1: 2: 3 majhne celotne številke (niti ne presegajo ducata).

Primeri zakona več razsežnosti

Za naslednje primere bodo uporabljeni isti prejšnji koraki, vendar bomo upoštevali molarne mase ustreznih elementov, ob predpostavki enega mola spojine.

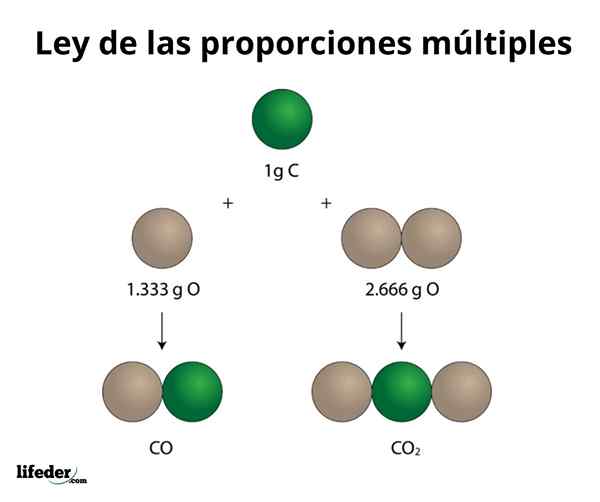
Kokosov oreh2

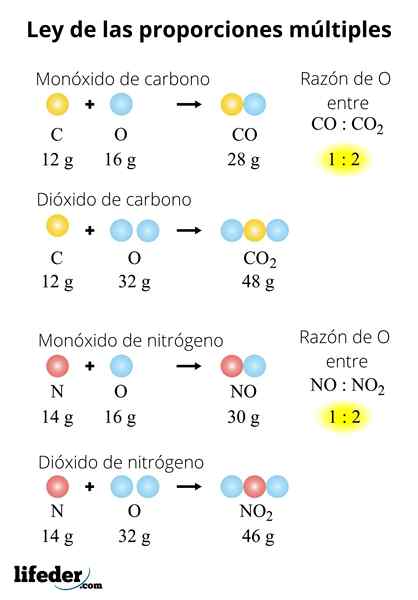
Ta primer na preprost način razloži, kako deluje zakon več razmer; V CO (ogljikov monoksid) je 1.333 gramov kisika za vsak gram ogljika. V ogljikovem dioksidu (CO₂) sta 2.666 gramov kisika za vsak gram ogljika. Zato je delež kisika v obeh spojinah 1: 2, majhno število celoštevilčnih številk.

H2O-h2Tudi2

Zakon o več razmerjih velja za par H2O-h2Tudi2.

Vam lahko služi: 30 primerov kemičnih suspenzij

V mol h2Ali, 2 grama vodika sta kombinirani s 16 grami kisika. Medtem v mol h2Tudi2, 2 grama vodika sta kombinirani z 32 grami kisika. Če želite preveriti, ali je ta zakon izpolnjen, moramo v obeh spojinah postaviti isto maso za enega od elementov. Ta čas je vodik: 2 grama.

Množični deleži za h2Ali in h2Tudi2 so:

  • H2O: 16 gramov ali/2 grama h
  • H2Tudi2: 32 gramov ali/2 grama h

Razmerje mase O bo 16:32. Vendar ga lahko poenostavimo tako, da delimo s 16 in ostanemo 1: 2. Spet je končni odnos sestavljen iz majhnih celih številk.

SW2-SW3

V molu SO2, 32 gramov žvepla je v kombinaciji z 32 grami kisika. Medtem v molu3, 32 gramov žvepla je v kombinaciji z 48 grami kisika. Žveplova masa je enaka za obe spojini, zato lahko neposredno primerjamo deleže kisika:

  • SW2: 32 gramov oz
  • SW3: 48 gramov oz

Je razmerje med kisikovo maso med obema spojinama, ki je enako 32:48 ali 1: 1.5. Toda ni bilo, da bi morale biti cele številke? Razmerje 1: 1.5 (1/1.5) Lahko ga zapišemo tudi kot 2: 3 (0.6) in spet bomo imeli majhne celotne številke: 2 in 3.

Upoštevajte, da bi lahko odnos napisali tudi kot 48:32 ali 1.5: 1, saj je rezultat 3: 2. Zakon se ne spreminja, le razlaga odnosa: 1 je 1.5 ali 3/2 krat več kisika v SO3 to v SO2; kar je enako reči, da je 2/3 ali 0.6 -krat manj kisika v SO2 to v SO3.

Ne št2-N2O-n2Tudi3-N2Tudi5

Zakon je mogoče uporabiti tudi za vrsto spojin. Razmislite o dušikovih oksidih: ne-ne2-N2O-n2Tudi3-N2Tudi5. Da bi ocenili ta zakon v njih, moramo postaviti množico dušika: 28 gramov. Ker? Ker ne in ne2 Imajo dušikov atom manj kot ostali oksidi:

  • 2 (št): 28 gramov n/32 gramov oz
  • 2 (št2): 28 gramov n/64 gramov oz
  • N2O: 28 gramov n/ 16 gramov oz
  • N2Tudi3: 28 gramov n/ 48 gramov oz
  • N2Tudi5: 28 gramov n/ 80 gramov oz
Lahko vam služi: hipofiza (H3PO2): lastnosti, uporabe in reagenti

Pozabimo na dušik in se osredotočimo na grame kisika:

  • 2 (ne): 32 gramov oz
  • 2 (št2): 64 gramov oz
  • N2O: 16 gramov oz
  • N2Tudi3: 48 gramov oz
  • N2Tudi5: 80 gramov oz

Je razmerje med masami ali enako 32: 64: 16: 48: 80. Da bi ga poenostavili, razdelimo vse njegovo število med najmanjšimi, 16, ki so kot 2: 4: 1: 3: 5.

To pomeni, da obstaja: 2 -krat več kisika v ne kot v n2Ali, 4 -krat več kisika v št2 da v n2Ali, 3 -krat več kisika v n2Tudi3 da v n2Ali in 5 -krat več kisika v n2Tudi5 da v n2Tudi. Spet imamo majhne cele številke, od 1 do 5.

Omejitve

Zakon več razsežnosti ni vedno izpolnjen. Na primer, molarne mase ali atomske teže elementov niso celotne številke, vendar imajo veliko decimalk. To popolnoma spremeni izračunane odnose, ki prenehajo biti preprosti.

Prav tako zakon ni izpolnjen za težke spojine, kot so nekateri ogljikovodiki. Na primer undecano, cenajstH24. 24, ima 1.0083 ali 121/120 -krat več vodika kot dekan, c10H22, katerih odnos je sestavljen iz 121 in 120, ki presegajo ducat; Niso majhne celotne številke.

In končno zakon ne uspe z nestohiometričnimi spojinami, kot pri številnih oksidih in sulfidih.

Zaključek

Zakon o več razmerjih navaja, da ko dva elementa tvorita več kot eno spojino, so različne mase elementa, ki se združujejo z isto maso drugega elementa, v deležu majhnega števila.

Reference

  1. Whitten, Davis, Peck & Stanley. (2008). Kemija. (8. izd.). Cengage učenje.
  2. Wikipedija. (2020). Zakon več razsežnosti. Pridobljeno iz: v.Wikipedija.org
  3. Uredniki Enyclopeedia Britannica. (2020). Zakon več razsežnosti. Okrevano od: Britannica.com
  4. Kemija. (4. junij 2019). Zakon več razsežnosti Daltona. Okrevano od: ChemistryGod.com
  5. Garcia nissa. (2020). Zakon več razmer: Opredelitev in primer. Študij. Okrevano od: študij.com