Pojasnilo prava Coulomb, formula in enote, vaje, poskusi

The Zakon Coulomb Fizični zakon ureja interakcijo med električno obremenjenimi predmeti. Navedel ga je francoski znanstvenik Charles Augustin de Coulomb (1736-1806), zahvaljujoč rezultatom njegovih poskusov s torzijsko bilanco.

Leta 1785 je Coulomb doživel nešteto časov z majhnimi električno nabitimi sferami, na primer, da je prinesla ali oddaljila dve sferi, ki spreminjajo velikost obremenitve in tudi njen znak. Vedno gledam in natančno registrirate vsak odgovor.

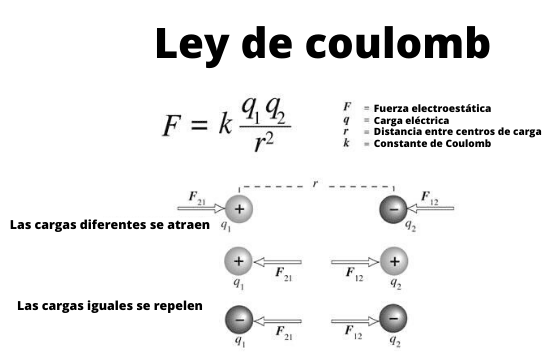
Slika 1. Shema, ki prikazuje interakcijo med specifičnimi električnimi naboji s Coulombovim zakonom.

Te majhne sfere lahko štejemo za posebne obremenitve, torej predmeti, katerih dimenzije so nepomembne. In izpolnjujejo, kot je znano že od časa starodavnih Grkov, da se odganjajo obremenitve istega znaka in privabljajo tiste z različnimi znaki.

Slika 2. Vojaški inženir Charles Coulomb (1736-1806) velja za najpomembnejšega fizika v Franciji. Vir: Wikipedia Commons.

Glede na to je Charles Coulomb našel naslednje:

-Sila privlačnosti ali odbojnosti med dvema specifičnimi naboji je neposredno sorazmerna z produktom obsega obremenitve.

-Ta sila je vedno usmerjena na črto, ki se pridruži obremenitvam.

-Končno je velikost sile obratno sorazmerna s kvadratom razdalje, ki ločuje obremenitve.

[TOC]

Formula in enote zakona Coulomb

Zahvaljujoč tem opažanjem je Coulomb ugotovil, da velikost sile F Med dvema posebnima nabojem q₁ in q₂, ločeno razdaljo r, Matematično je dano kot:

Ker je sila vektorska velikost, da jo izrazimo, je enotni vektor v celoti definiran r V smeri črte, ki se pridruži obremenitvam (enotni vektor ima velikost, enaka 1).

Poleg tega se nenehna konstantna sorazmernost pretvori prejšnji izraz v enakost K imenujemo K_in ali preprosto k: Elektrostatična konstanta tudi Coulomb konstanta.

Končno je vzpostavljen zakon Coulomb za točne obremenitve, ki ga daje:

Sila, kot vedno v mednarodnem sistemu enot, prihaja v Newtonu (N). Kar zadeva naboje, se enota imenuje Coulomb (c) v čast Charlesa Coulomba in na koncu razdalja r prihaja v metrih (m).

Pozorno opazovanje prejšnje enačbe je jasno, da mora imeti elektrostatična konstanta enote n.m² / C², Za pridobitev Newtonov kot rezultat. Vrednost konstante je bila določena eksperimentalno kot:

Vam lahko služi: brezplačni vektorji: lastnosti, primeri, vaje

k_in = 8.89 x 10 ⁹ N.m² / C² ≈ 9 x 10 ⁹ N.m² / C²

Slika 1 prikazuje interakcijo med dvema električnimi naboji: ko sta isti znak, ki sta ga odvrženi, sicer pritegnejo.

Upoštevajte, da Coulombov zakon ustreza Newtonovemu tretjemu zakonu ali zakonu o ukrepanju in reakciji, torej veličini F₁ in F₂ So enaki, naslov je enak, toda čutila so nasprotna.

Kako uporabiti Coulombov zakon

Za reševanje interakcij med električnimi naboji je treba upoštevati naslednje:

- Enačba se uporablja izključno v primeru specifičnih obremenitev, to je električno obremenjenih predmetov, vendar zelo majhnih dimenzij. Če imajo naloženi predmeti merljive dimenzije, jih je treba razdeliti na zelo majhne obremenitve in nato dodati prispevke vsake od teh obremenitev, za katere je potreben celovit izračun.

- Električna sila je vektorska velikost. Če medsebojno delujeta več kot dve naboji, neto sila na obremenitvi Q_Yo Daje načelo superpozicije:

F_Mreža = F_i1 + F_I2 + F_i3 + F_i4 +… = ∑ F_ij

Kjer je naročnik J Vale 1, 2, 3, 4 ... in predstavlja vsako od preostalih obremenitev.

- Vedno mora biti skladen z enotami. Najpogosteje je delo z elektrostatično konstanto v enotah, če se morate prepričati, da so obremenitve v coulombu in razdalje v metrih.

- Končno se enačba uporablja, ko so obremenitve v statičnem ravnovesju.

Rešene vaje

- Vaja 1

Na naslednji sliki obstajata dve posebni obremenitvi +Q in +2Q. Tretja točna obremenitev -Q je nameščena na P. Zaradi prisotnosti drugih se zahteva, da najde električno silo na tej obremenitvi.

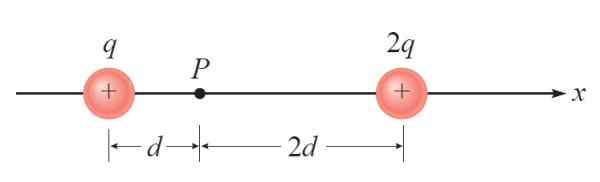Slika 3. Diagram za leto rešeno 1. Vir: Giambattista, a. Fizika.

Rešitev

Prva stvar je vzpostaviti ustrezen referenčni sistem, ki je v tem primeru vodoravna os ali x -osi. Izvor tega sistema je lahko kjer koli, vendar bo v udobju nameščen v P, kot je prikazano na sliki 4A:

Vam lahko služi: bethelgeuse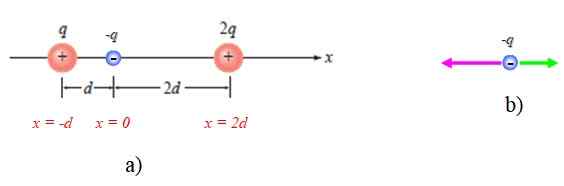Slika 4. Shema za leto rešena 1. Vir: Giambattista, a. Fizika.

Prikazana je tudi shema sil na -Q, ob upoštevanju, da jo privlačita druga dva (slika 4B).

Pokličimo F₁ Na silo, ki izvaja obremenitev, ki je na obremenitvi -Q, so usmerjeni vzdolž osi x in točke v negativnem smislu:

Vektor enote v smeri osi x je x Z naglasom Circusflex v enačbi. To je pogost zapis za enotni vektor. Manj se pojavi, ker je sila F₁ točke v negativnem pomenu osi.

Analogno se izračuna F₂:

Upoštevajte, da je velikost F₂ Je polovica F₁, Čeprav je obremenitev dvojna. Da bi našli neto silo, jih končno dodajamo F₁ in F₂:

F_Mreža = (-K + K/2).(Q² /d²) (x) N = - (k/2).(Q² /d²) (x) N

- Vaja 2

Dva polistirenska sferita enake mase M = 9.0 x 10^-8 kg ima enako pozitivno obremenitev q in je suspendirana s svileno nitjo v dolžini l = 0,98 m. Kroglice so ločene na razdalji d = 2 cm. Izračunajte vrednost.

Rešitev

Položaj izjave je opisan na sliki 5A.

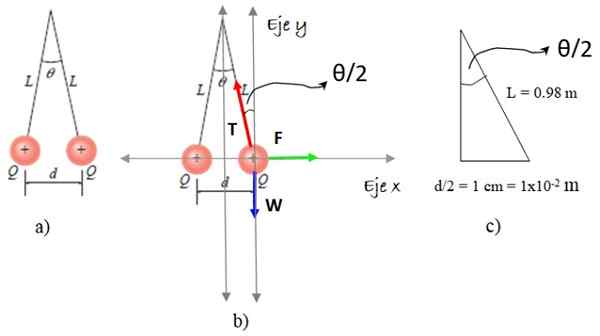Slika 5. Sheme za reševanje vaje 2. Vir: Giambattista, a. Fizika /f. Zapata.

Izbrali smo eno od sferitov in na njej narišemo izolirani shema telesa, ki vključuje tri sile: teža W, Napetost vrvi T in elektrostatično odbojnost F, Kot je prikazano na sliki 5b. In zdaj koraki:

Korak 1

Vrednost θ/2 se izračuna s trikotnikom slike 5c:

θ/2 = arcsen (1 x 10^-2/0.98) = 0.585 °

2. korak

Potem morate uporabiti Newtonov drugi zakon in tekmo 0, saj so stroški v statičnem stanju. Pomembno je poudariti, da napetost T Naklonjen je in ima dve komponenti:

∑f_x = -T.sin θ + f = 0

∑f_in = T.cos θ - w = 0

Korak 3

Očistimo velikost napetosti zadnje enačbe:

Lahko vam služi: dinamika: zgodovina, kakšne študije, zakoni in teorije

T = w/ cos θ = mg/ cos θ

4. korak

Ta vrednost se nadomesti v prvi enačbi, da bi našli velikost F:

F = t sin θ = mg (sin θ / cos θ) = mg. TG θ

5. korak

Kot f = k q² /d², Počisti Q:

Z nadomeščanjem številčnih vrednosti, ki jo zagotavlja izjava, se dobi:

Q = 2 × 10^-enajst C.

Poskusi

Preverjanje Coulombovega zakona je preprosto s torzijskim ravnovesjem, podobno tistemu, ki se uporablja v njegovem laboratoriju.

Obstajata dve majhni sferi Saúco, od katerih je ena, ena v središču ravnotežja, suspendirana iz niti. Eksperiment je sestavljen v dotik kroglic Saúco, prenesenih z drugo kovinsko sfero, naloženo z obremenitvijo Q.

Slika 6. Coulombovo torzijsko ravnovesje.

Takoj se obremenitev razporedi med obema sferama Saúco, toda potem, kot sta tovora istega znaka, odbijata. Sila, ki povzroči torzijo niti iz niti in se takoj oddalji od fiksne krogle, deluje na suspendirano sfero.

Potem vidimo, da sega nekajkrat, dokler ravnotežje ne doseže. Potem je torzija palice ali niti, ki jo drži.

Če bi bile sfere prvotno na 0, bo zdaj mobilna krogla obrnila kot θ. Obseg ravnotežja je v stopinjah diplomirani trak za merjenje tega kota. Ko predhodno določamo torzijsko konstanto, se potem odbojna sila in vrednost obremenitve, ki jo pridobijo Saúcove krogle, enostavno izračunati.

Reference

1. Figueroa, d. 2005. Serija: Fizika za znanost in inženiring. Zvezek 5. Elektrostatika. Uredil Douglas Figueroa (USB).
2. Giambattista, a. 2010. Fizika. Druga izdaja. McGraw Hill.
3. Giancoli, d.  2006. Fizika: načela z aplikacijami. 6. Ed Prentice Hall.
4. Resnick, r. 1999. Fizično. Vol. 2. 3. izd. v španščini. Continental uredništvo s.Do. od c.V.
5. Sears, Zemansky. 2016. Univerzitetna fizika s sodobno fiziko. 14. Ed. Zvezek 2.