Ampère Zakon o formuli in enačbah, demonstracije, vaje

The Ampère zakon navaja, da kroženje vektorja magnetne indukcije B Sorazmerna je z intenzivnostjo in tokom, ki teče po istem.

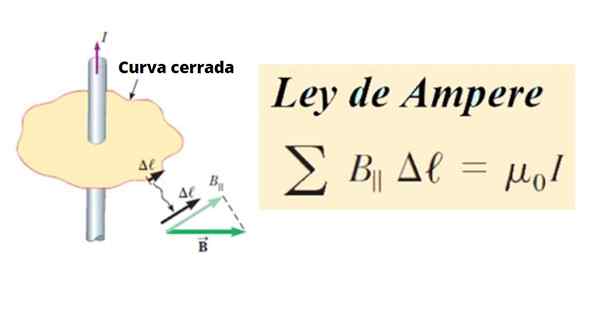
Po vrsti B Je vsota vseh izdelkov med tangencialno komponento B_║ in dolžino majhnega segmenta Δℓ zaprte krivulje c, Okoli vezja. V matematičnem smislu je napisano tako:

∑ b_║ .Δℓ ∝ Yo

Slika 1. Opredelitev zakona o amperih. Vir: Serway, r. Fizika na fakulteti.

Kot poljubna linija ali krivulja jo lahko razdelimo na majhne segmente Δℓ, In ti so lahko neskončno majhni, potem jih imenujemo Dℓ.

V tem primeru vsota postane sestavna linija skalarnega izdelka med vektorji B in ds. Ta izdelek vsebuje tangencialno komponento B, ki je B cosθ, kjer je θ kot med vektorji:

Majhen krog, ki prečka integral, pomeni, da se integracija izvaja na zaprti poti C, kar v tem primeru vključuje tok, ki teče skozi voznikov presek.

Konstanta sorazmernosti, ki je potrebna za določitev enakosti, je μ_tudi, Vakuumska prepustnost. Na ta način ostaja Ampèrejev zakon:

Ampèrejev zakon nam pravi, da je linija integral ∫_C B ∙ ds Vredno je natančno μ_tudiJaz, vendar nam ne ponuja podrobnosti o tem, kako je usmerjeno magnetno polje B Glede krivulje C na vsaki točki ali o tem, kako izračunati integral. Pove nam le, da je rezultat istega vedno μ_tudiYo.

[TOC]

Demonstracija zakona Ampère

Ampèreov zakon preverja eksperimentalno preverjanje magnetnega polja, ki ga proizvaja zelo dolg pravokotni prevodnik. Preden se odpravite na težavo, je treba izpostaviti dva primera, ki sta posebna interesa v prejšnji enačbi:

Lahko vam služi: svetlobna telesa: značilnosti in kako ustvarjajo svojo svetlobo

-Prva je, kdaj B in ds So vzporedni, kar to pomeni B je tangencialno do c. Potem je kot med obema vektorji 0 ° in skalarni izdelek je preprosto produkt velikosti B.ds.

-Drugi se pojavi, če B in ds So pravokotne, v tem primeru je skalarni izdelek 0, saj je kot med vektorji 90 °, katerih kosinus je 0.

Druga pomembna podrobnost je izbira krivulje c, na kateri se ocenjuje kroženje polja. Ampèrejev zakon ne določa, kaj je lahko, vendar mora zaviti trenutno distribucijo. Prav tako ne piše, kako potovati krivuljo in za to obstajata dve možnosti.

Rešitev je dodelitev znakov po pravilu pravilnega palca. Štirje prsti so ukrivljeni v smeri, v katero želite integrirati, ponavadi bo to na terenu enako B kroži. Če trenutne točke v smeri desnega palca, je dodeljen znak in če ne, podpis -.

To velja, kadar obstaja porazdelitev z več tokovi, nekateri so lahko pozitivni in drugi negativni. Algebrska vsota le -teh je tisto, kar bomo dali v zakon Ampère, ki je običajno imenovana kot Neizrečen tok (Za krivuljo c).

Magnetno polje pravokotne in neskončne žice

Slika 2 prikazuje žico, ki prevaža tok in zunaj letala. Pravo pravilo palca to zagotavlja B Kroži v nasprotni smeri in opisuje obode, kot kažejo rdeče puščice.

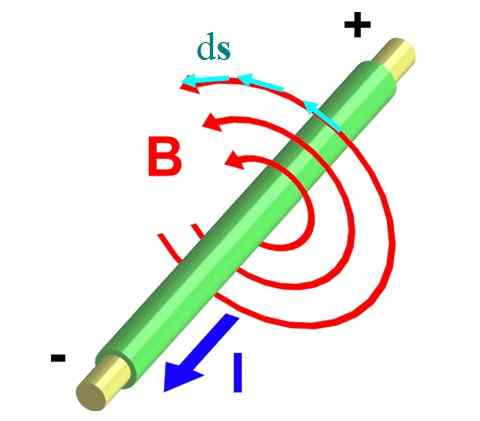Slika 2.- Magnetno polje neskončne žice. Vir: Wikimedia Commons.

Vzemimo enega od njih, katerega polmer je r. Razdelimo ga na majhne diferencialne segmente ds, predstavljen z modrimi vektorji. Oba vektorja, B in ds, So vzporedni na vsaki točki oboda in na ta način integral ∫_C B ∙ ds Se spremeni v:

Vam lahko služi: neposredni tok

∫_C Bds

To je zato, ker, kot smo že rekli, skalarni izdelek B ∙ ds  Je produkt velikosti vektorjev s kosinusom 0 °. Rezultat integrala je znan po zakonu Ampère, zato pišemo:

∫_C Bds = μ_tudiYo

Ker je velikost polja konstantna po celotni poti, pušča integral:

B ∫_C Ds = μ_tudiYo

Integral ∫_C DS predstavlja vsoto vseh neskončnih majhnih segmentov, ki sestavljajo obseg radia r, Enakovreden svoji dolžini, produkt njegovega polmera za 2π:

B.2πr = μ_tudiYo

In od tam ugotovimo, da je velikost B:

B = μ_tudiI / 2πr

Poudariti je treba, da tudi če izbrana usmeritev (ali amperijski vezje) Ne krožni, rezultat integrala je še naprej μ_tudiJaz pa ∫_C B ∙ ds Ne bi bil več b.2πr.

Zato je uporabnost Ampèrejevega zakona za določitev magnetnega polja pri izbiri porazdelitev z visoko simetrijo, tako da je integral enostavno oceniti. Krožne in pravokotne usmeritve izpolnjujejo to zahtevo.

Rešene vaje

- Vaja 1

Razmislite o krivuljah A, B, C in D, prikazane na sliki 3. Zavijejo tri tokove, dva, ki zapuščata letalo, simbolizirana z eno točko ( . ), katerih intenzivnosti sta 1 A in 5 A, in tok, ki vstopi v letalo, ki je označen s križem in katerih velikost je 2 a.

Poiščite tok, priložen vsaka krivulja.

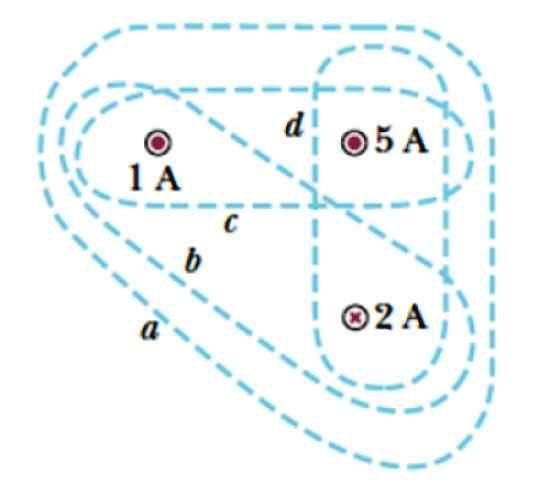Slika 3. Več krivulj za uporabo zakona Ampère. Vir: Serway, r. Fizika na fakulteti.

Rešitev

Tokovi, ki zapustijo papir, so dodeljeni znak +. V skladu s tem:

Lahko vam služi: površinski valovi: značilnosti, vrste in primeri

Krivulja a

Obdaja tri tokove, zato je zaprt tok + 1 a + 5 a - 2 a = 4 a.

Krivulja b

Samo tokovi 1 a y - 2 a so znotraj te krivulje, zato je zaprti tok iz - 2 a.

Krivulja c

Vsebuje odhodne tokove 1 in 5 a, zato je zaprt tok 6 a.

Krivulja d

Tokovi v notranjosti so +5 a in - 2 a, nato pa obdajajo neto tok od 3 do.

- Vaja 2

Izračunajte velikost magnetnega polja, ki ga proizvaja zelo dolga pravokotna žica.

Rešitev

Po Ampèrejevem zakonu je žično polje podano z:

B = μ_tudiI / 2πr = (4π x 10^-7 x 1/2π x 1) t = 2 x 10^-7 T.

Reference

1. Figueroa, d. (2005). Serija: Fizika za znanost in inženiring. Zvezek 6. Elektromagnetizem. Uredil Douglas Figueroa (USB).
2. Vitez, r.  2017. Fizika za znanstvenike in inženiring: strateški pristop.  Pearson.
3. Sears, Zemansky. 2016. Univerzitetna fizika s sodobno fiziko. 14. Ed. Zvezek 2.
4. Serway, r. 2009. Fizika na fakulteti. Cengage učenje.
5. Tipler, str. (2006) Fizika za znanost in tehnologijo. 5. izd. Zvezek 2. Uredništvo se je vrtelo.