Elastična sila, kar je sestavljeno, formule in vaje

The elastična sila Sila je, da se predmet upira spremembi v svoji obliki. Se manifestira v predmetu, ki se ponavadi okreva, ko je pod delovanjem deformacijske sile.

Elastična sila se imenuje tudi obnovitvena sila, ker nasprotuje deformaciji, da bi objekte vrnili v ravnotežni položaj. Prenos elastične sile je skozi delce, ki integrirajo predmete.

Elastična moč vzmeti

Na primer, ko je stisnjena kovinska vzmet, se sila, ki potisne vzmetne delce.

Če se namesto stiskanja vzmeti vrže, se raztezajo, delci, ki ga integrirajo. Prav tako se delci upirajo ločitvi sile v nasprotju z raztezanjem.

Predmeti, ki imajo lastnost izterjave prvotne oblike z nasprotnimi sili deformacije, se imenujejo elastični predmeti. Vzmeti, elastične gume in elastične strune so primeri elastičnih predmetov.

[TOC]

Kaj je elastična sila?

Elastična sila (F_k) Silo je, da predmet izvaja, da si povrne svoje naravno ravnovesje, tako da je vplivala zunanja sila.

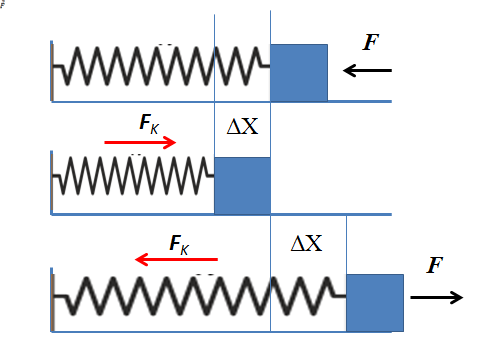
Za analizo elastične sile bo upoštevan idealen sistem spomladanske mase, ki je sestavljen iz vodoravno postavljenega vzmeti, ki je pod enim koncem na steni, na drugem koncu pa do bloka zaničevalne mase. Druge sile, ki delujejo na sistem, kot sta trenje ali silo gravitacije, ne bodo upoštevane.

Lahko vam služi: drugo ravnotežno stanje: razlaga, primeri, vaje

Če se na testo izvaja horizontalna sila, usmerjena proti steni, se prenese v vzmet, ki ga stisne. Pomlad se premika iz ravnotežnega položaja proti novemu položaju. Ker predmet ponavadi ostane v ravnovesju, se spomladi manifestira elastična sila, ki nasprotuje uporabljeni sili.

Premik kaže, koliko sta bila vzmet in elastična sila deformirana sorazmerna s tem premikom. Ko se vzmet stisne, se spreminjanje položaja povečuje in posledično poveča elastično silo.

Bolj ko je vzmet stisnjena, več opozicijske sile deluje, dokler ne doseže točke, kjer sta uporabljena sila in elastična sila uravnotežena, posledično se spomladanska masa neha premikati. S ustavitvijo moči je edina sila, ki deluje elastična sila. Ta sila pospeši vzmet v smeri v nasprotju z deformacijo, dokler ne povrne stanja ravnotežja.

Na enak način se pojavi pri raztezanju vzmeti in opazujejo vodoravno. Pomlad je raztegnjena in takoj izvaja silo, sorazmerno z raztezanjem, ki nasprotuje raztezanju.

Formule

Formula elastične sile je izražena z zakonom Hooke. Ta zakon določa, da je linearna elastična sila, ki jo ima predmet.

F_k = -k.Δs         [1]

F_k = Elastična sila

k = Konstantna sorazmernost

Δs = Premik

Ko se predmet premakne vodoravno, kot v primeru vzmeti, ki je pod steno, je premik Δx, In izraz Hookeovega zakona je napisan:

F_k = -k.Δx        [2]

Vam lahko služi: konvergentna leča: značilnosti, vrste in reševanje vadbe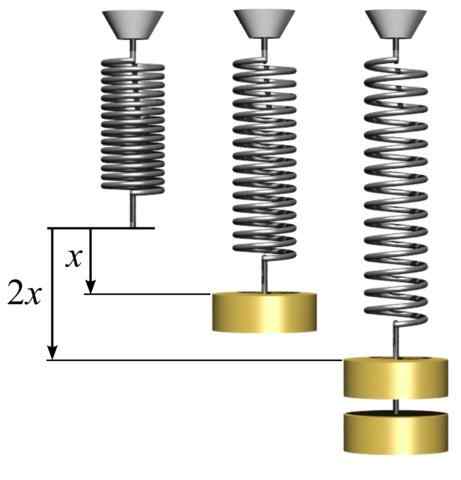Hookejev zakon. Elastična sila sorazmerna z raztezanjem. [Avtor svjo (https: // commons.Wikimedia.org/wiki/datoteka: kljukice.Png)]

Negativni znak v enačbi kaže, da je elastična sila vzmeti v nasprotni smeri do sile, ki je povzročila premik. Konstantna sorazmernost k To je konstanta, ki je odvisna od vrste materiala, na katerega je sestavljena vzmet. Enotnost konstante k je N/m.

Elastični predmeti imajo mejo elastičnosti, ki bo odvisna od konstante deformacije. Če se razteza čez mejo elastike, se bo trajno deformirala.

Enačba [1] in [2] velja za majhne vzmetne premike. Ko so premiki večji, se izrazi z večjo močjo Δx.

Kinetična energija in potencialna energija, ki sta se nanašala na elastično silo

Elastična sila deluje na pomladi, tako da jo premakne v ravnotežni položaj. Med tem procesom se potencialna energija spomladanskega masnega sistema poveča. Potencialna energija zaradi dela elastične sile je izražena v enačbi [3].

U = ½ K .  Δx²[3]

Potencialna energija je izražena v joulesu (j).

S prenehanjem uporabe deformacijske sile se vzmet pospeši na ravnotežni položaj z zmanjšanjem potencialne energije in povečanjem kinetične energije.

Kinetična energija spomladanskega masnega sistema, ko doseže ravnotežni položaj, je določena z enačbo [4].

In_k= ½ m.v²[4]

m = masa

v = spomladanska hitrost

Za reševanje sistema spomladanske mase se uporablja drugi zakon Newtona, ob upoštevanju, da je elastična sila spremenljiva sila.

Praktične vaje primerov

Pridobivanje sile deformacije

Koliko sile je potrebno, da se nanaša na vzmet, da se raztegne 5 cm, če je vzmetna konstanta 35n/m?

Vam lahko služi: pospeševanje gravitacije: kaj je to, kako se meri in vaje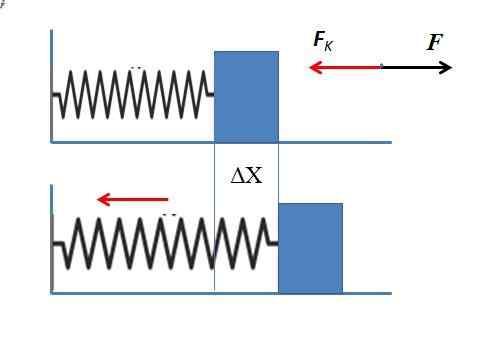Elastična sila vzmeti, ki se razteza 5 cm

Ker je sila uporabe nasprotna elastični sili F_k Ob predpostavki, da je vzmet raztegnjena vodoravno. Rezultat ne zahteva negativnega znaka, saj je potrebna samo sila prijave.

Hookejev zakon

F_k = -k.Δx       

Stalnica k pomladi je 35n/m.

Δx = 5cm = 0,05m

F_k = -35n/m . 0,05m

F_k = - 1,75n = - f

Potreben 1,75 n sile za deformiranje pomladi 5cm.

Pridobivanje konstante deformacije

Kakšna je deformacijska konstanta vzmeti, ki se razteza 20 cm z delovanjem sile 60n?

Δx =20cm = 0,2 m

F = 60n

F_k = -60n = - f

K = - f_k / Δx

  = -(-60n) /0.2m

K = 300 n/m

Vzmetna konstanta je 300n/m

Pridobivanje potencialne energije

Kakšna je potencialna energija, ki jo nanašajo elastična sila vzmeti, ki je stisnjena 10cm In njegova konstanta deformacije je 20n/m?

Δx =10 cm = 0,1m

K = 20 n/m

F_k = -20n/m . 0,1m

F_k = -200n

Elastična sila pomladi je -200n.

Ta sila deluje na pomladi, da jo premakne v ravnotežni položaj. Pri opravljanju tega dela se potencialna energija sistema poveča.

Potencialna energija se izračuna z enačbo [3]

U = ½ K .  Δx²

U = ½ (20n/m) . (0,1m)²

U = 0,1Joules

Reference

1. Kittel, C, Knight, W D in Ruderman, M A. Mehanika. ZDA: Mc Graw Hill, 1973, Vol. Yo.
2. Rama Reddy, K, Badami, S B in Balasubramanian, V. Oscilamenti in valovi. Indija: University Press, 1994.
3. Murphy, J. Fizika: neprekinjenost lastnosti snovi in ​​energije. New York: Britannica Educational Publishing, 2015.
4. Giordano, n J. Fizika na fakulteti: sklepanje in odnosi. Kanada: Brooks/Cole, 2009.
5. Walker, J, Halliday, D in Resnick, R. Osnove fizike. ZDA: Wiley, 2014.