Vrste trenja, koeficient, izračun, vaje

The trenje To je odpornost na premik ene površine, medtem ko je v stiku z drugo. Gre za površinski pojav, ki se pojavlja med trdnimi, tekočimi in plinastimi materiali. Tangencialna odpornost na dve površini v stiku, ki nasprotuje smeri relativnega premika med temi površinami, se imenuje tudi trenje ali trenje sile F_r.

Za izpodbijanje trdnega telesa na površini je treba uporabiti zunanjo silo, ki lahko premaga trenje. Ko se telo premakne, sil trenja deluje na telesu, ki zmanjšuje hitrost in ga lahko celo ustavi.

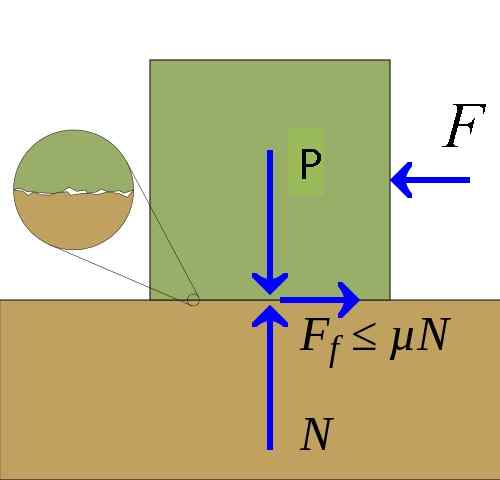
Trenje [avtor Keta, Pietter Kuiper (https: // commons.Wikimedia.org/wiki/datoteka: trenje.SVG)]

Sila trenja je lahko grafično predstavljena s pomočjo sil diagrama telesa v stiku s površino. V tem diagramu sile trenja F_r Nariše ga komponenta sile, nanesene na tangencialno telo na površino.

Kontaktna površina izvaja reakcijsko silo na telesu, imenovano normalna sila N. V nekaterih primerih je normalna sila posledica teže Str telesa, ki počiva na površini, v drugih primerih.

Trenje izvira, ker obstajajo mikroskopski rugosi med površinami v stiku. Ko poskušate premakniti eno površino na drugo. Izgube energije nastajajo v obliki toplote, ki se ne uporablja za premikanje telesa.

[TOC]

Vrste trenja

Obstajata dve glavni vrsti trenja: trenje Coulomb o Trenje suhega in trenje tekočine.

-Trenje Coulomb

Trenje Coulomb Vedno nasprotuje gibanju teles in je razdeljen na dve vrsti trenja: statično trenje in kinetično (ali dinamično) trenje.

V statičnem trenju ni gibanja telesa na površini. Uporabljena sila je zelo nizka in ni dovolj za premagovanje sile trenja. Trenje ima največjo vrednost, ki je sorazmerna z normalno silo in se imenuje statična trenja F_oferi.

Statična sila trenja je opredeljena kot največja sila, ki se upira na začetku gibanja telesa. Ko uporabljena sila presega statično trenje, ostane na največji vrednosti.

Kinetično trenje deluje, ko je telo v gibanju. Sila, potrebna za ohranitev telesa s trenjem, se imenuje kinetična trenja sila F_RC.

Kinetična trenja je manjša ali enaka statičnemu trenju, ker ko se telo začne premikati.

Coulomb zakoni o trenju

1. Sila trenja je neposredno sorazmerna z normalno silo na kontaktno površino. Konstanta sorazmernosti je koeficient trenja μ ki obstaja med površinami v stiku.
2. Sila trenja je neodvisna od velikosti navideznega kontaktnega območja med površinami.
3. Kinetična trenja je neodvisna od hitrosti drsenja telesa.

-Trenje tekočine

Trenje se pojavi tudi, ko se trupla premikajo v stiku s tekočimi ali plinastimi materiali. Ta vrsta trenja se imenuje trenje tekočine in je opredeljeno kot odpornost proti gibanju teles v stiku s tekočino.

Lahko vam služi: Easy Physics Experiments (primarna univerza)

Trenje tekočine se nanaša tudi na odpornost tekočine, ki se pretaka v stik s plastmi tekočine istega materiala ali drugačnega in je odvisna od hitrosti in viskoznosti tekočine. Viskoznost je merilo odpornosti na gibanje tekočine.

-Trenje Stokes

Trenje Stokes je vrsta trenja tekočine, v katerem sferični delci potopljeni v viskozno tekočino, v laminarnem toku, doživljajo silo trenja, ki upočasni njegovo gibanje zaradi nihanj molekul tekočine.

Stokes Trenje [avtor Kraaiennest (https: // commons.Wikimedia.org/wiki/datoteka: stokes_sphere.SVG)]

Pretok je laminarni, ko so viskozne sile, ki nasprotujejo gibanju tekočine, večje od inercialnih sil in se tekočina premika z dovolj majhno hitrostjo in v pravokotni poti.

Koeficienti trenja

V skladu s prvim zakonom trenja Coulomb Koeficient trenja μ Dobimo iz razmerja med silo trenja in normalno silo do kontaktne površine.

μ = f_r/N

Koeficient μ To je brezdimenzionalna količina, saj gre za razmerje med dvema silama, ki je odvisno od narave in zdravljenja materialov v stiku. Na splošno je vrednost koeficienta trenja med 0 in 1.

Statični koeficient trenja

Statični koeficient trenja je konstanta sorazmernosti, ki obstaja med silo, ki preprečuje gibanje telesa v stanju stika na kontaktni površini in normalno silo na površino.

μ_in= F_oferi/N

Kinetični koeficient trenja

Kinetični koeficient trenja je konstanta sorazmernosti, ki obstaja med silo, ki omejuje gibanje telesa, ki se premika na površini, in normalno silo na površino.

μ_c= F_RC/N

Statični koeficient trenja je večji od kinetičnega koeficienta trenja.

μ_s> μ_c

Koeficient elastičnega trenja

Koeficient elastičnega trenja izhaja iz trenja med kontaktnimi površinami elastičnih, mehkih ali grobih materialov, ki jih deformirajo uporabljene sile. Trenje nasprotuje relativnemu gibanju med dvema elastičnimi površinami in premikom spremlja elastična deformacija površinskih plasti materiala.

Koeficient trenja, pridobljenega v teh pogojih, je odvisen od stopnje hrapavosti površine, od fizikalnih lastnosti kontaktnih materialov in velikosti tangencialne komponente slinske sile v vmesniku materiala.

Koeficient molekularnega trenja

Koeficient molekularnega trenja dobimo iz sile, ki omejuje gibanje delca, ki drsi na mehki površini ali skozi tekočino.

Kako se izračuna trenje?

Sila trenja v trdnih vmesnikih se izračuna z enačbo F_r = μN

N To je normalna sila in μ To je koeficient trenja.

V nekaterih primerih je normalna sila enaka teži telesa Str. Teža dobimo z množenjem mase m telesa zaradi pospeška gravitacije g.

Str= mg

Z nadomeščanjem enačbe teže v enačbi sile trenja se pridobi:

Lahko vam služi: povprečni pospešek: kako se izračuna in reši

F_r = μmg

Normalne lastnosti

Ko je predmet v mirovanju na ravni površini, je običajna sila tista, ki izvaja površino na telesu in nasprotuje sili zaradi gravitacije, v skladu z Newtonovim zakonom o delovanju in reakciji.

Normalna sila vedno deluje pravokotno na površino. Na nagnjeni površini se normalno zmanjšuje, ko se kot naklona povečuje in kaže v pravokotno smeri stran od površine, medtem ko teže navpično navzdol. Običajna enačba sile na nagnjeni površini je:

N = mgcosθ

θ = kot naklona kontaktne površine.

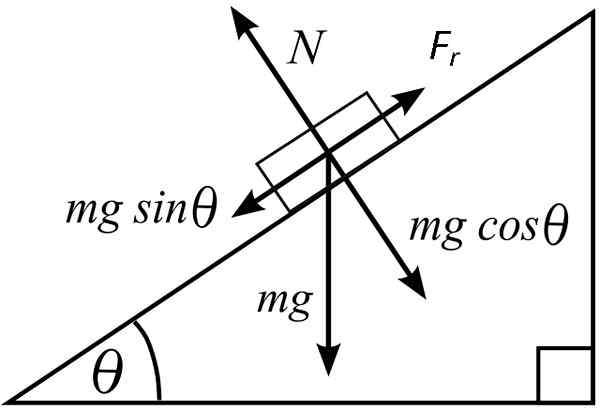Trenje v nagnjeni ravnini [avtor Mets501 (https: // commons.Wikimedia.org/wiki/datoteka: free_body.SVG)]

Sestavni del sile, ki deluje na telo, da drsi, je:

F = mgsenθ

Ko se uporabljena sila poveča na največjo vrednost sile trenja, ta vrednost ustreza statični sili trenja. Kdaj  F = f_oferi, Statična sila trenja je:

F_oferi= mgsenθ

In koeficient statičnega trenja dobimo s tangentom naklonskega kota θ.

μ_in = tanθ

Rešene vaje

-Trenska sila predmeta, ki počiva na vodoravni površini

15kg škatlo, nameščeno na vodoravni površini. Določite statične in kinetične koeficiente trenja.

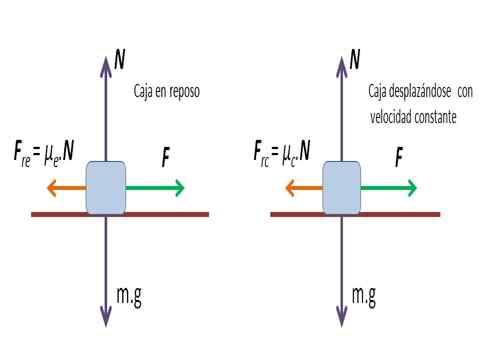Škatla, ki se giblje na vodoravni površini

Rešitev: Z vrednostjo uporabljene sile za premikanje polja dobimo statični koeficient trenja μ_in.

μ_in= F_oferi/N

Normalna sila N na površino je enaka teži škatle, torej N = m.g

N = 15kgx9,8m/s²

N = 147New

V tem primeru, μ_in= 50New/147New

μ_in= 0,34

Uporabljena sila za vzdrževanje hitrosti konstantne škatle je kinetična trenja, ki je enaka 25.

Koeficient kinetičnega trenja dobimo z enačbo μ_c= F_RC /N

μ_c= 25New/147New

μ_c= 0,17

-Trenska sila predmeta pod delovanjem sile s kotom naklona

Moški uporabi silo za 20 kilogramov s kotom nanosa 30 ° glede na površino, kjer počiva. Kakšna je velikost uporabljene sile za premikanje škatle, če je koeficient trenja med škatlo in površino 0,5?

Rešitev: Uporabljena sila in njene navpične in vodoravne komponente so predstavljeni v diagramu prostega telesa.

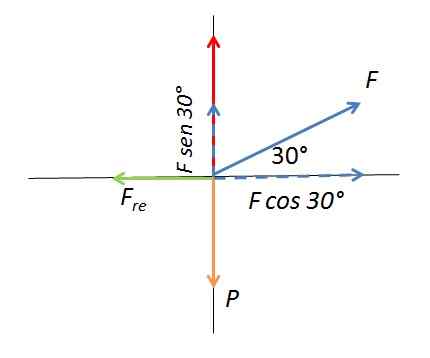Diagram prostega telesa

Uporabljena sila tvori kot 30 ° z vodoravno površino. Vertikalna komponenta sile doda normalno silo, ki vpliva na statično silo trenja. Polje se premika, ko vodoravna komponenta uporabljene sile presega največjo vrednost sile trenja F_oferi. Z ujemanjem vodoravne komponente sile s statičnim trenjem se dobi:

F_oferi = Fcosθ                       [1]

F_oferi= μ_in.N                          [2]

Lahko vam služi: Rutherford Atomski model: Zgodovina, poskusi, postulati

μ_in.N = fcosθ                      [3]

Normalna moč

Normalna sila ni več teža telesa zaradi navpične komponente sile.

Po Newtonovem drugem zakonu je vsota sil, ki delujejo na polje na navpični osi, praznina, zato je navpična komponenta pospeška do_in= 0. Običajna sila dobimo iz vsote

F Sen30 ° + N - P = 0                      [4]

P = m.g                                        [5]

F snn 30 ° + n - m.G = 0                [6]

N = m.G - F Sen 30 °                      [7]

Pri zamenjavi enačbe [7] v enačbi [3] dobimo naslednje:

μ_in. (m.G - f sin 30 °) = fcos30 °     [8]

Razčisti F Iz enačbe [8] in pridobljeno:

F = μ_in . m.G /(cos 30 ° + μ_in greh 30 °) = 0,5 x 20kg x 9,8m/s² / (0,87+ (0,5 x 0,5)) =

F = 87,5New

-Trenje v premičnem vozilu

1,5 tone vozilo se premika na pravokotni in vodoravni cesti s hitrostjo 70 km/h. Voznik na določeni razdalji vizualizira ovire na cesti, ki ga prisili, da se ostro ustavi. Po zaustavitvi drsalnega vozila za kratek čas, dokler se ne ustavi. Če je koeficient trenja med pnevmatikami in cesto 0,7; Določite naslednje:

1. Kakšna je vrednost trenja med vozilom patine?
2. Pojemka vozila
3. Razdalja, ki jo vozilo prevozi s postankov, dokler se ne ustavi.

Rešitev:

Oddelek a

Diagram prostega telesa prikazuje sile, ki delujejo na vozilu pri drsanju.

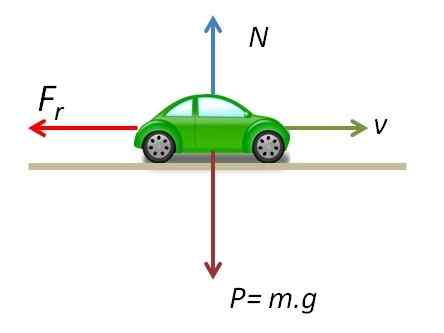Sile, ki delujejo v premičnem vozilu

Ker je vsota sil, ki delujejo v navpični osi, enaka nič, je normalna sila enaka teži vozila.

N = m.g

M = 1,5 tona = 1500kg

N = 1500kgx9,8m/s²= 14700New

Sila trenja vozila pri drsanju je:

F_r = μn = 0,7x14700New

= 10290 NOVO

Oddelek b

Sila trenja vpliva na zmanjšanje hitrosti vozila pri drsanju.

Pri uporabi Newtonovega drugega zakona se vrednost pojemka pridobi s čiščenjem enačbe F = m.do

A = f/m

a = (-10290 novih)/ 1500kg

= -6,86m/s²

Oddelek c

Začetna hitrost vozila je v₀ = 70km/h = 19,44m/s

Ko vozilo ustavi končno hitrost v_F = 0 In upočasnjevanje je a = -6,86m/s²

Razdalja, ki jo prevozi vozilo, saj se ustavi, dokler se ne ustavi, dobimo s čiščenjem d naslednje enačbe:

v_F² = v₀²+2AD

D = (v_F² - v₀²)/2a

= ((0)²-(19,44m/s)²)/(2x (-6,86m/s²)

D = 27,54m

Vozilo potuje 27.54m razdalja pred ustavitvijo.

 Reference

1. Izračuni koeficienta trenja pod pogoji elastičnega stika. Mikhin, n m. 2, 1968, Sovjetska znanost o materialih, Vol. 4, str. 149-152.
2. Blau, P J. Znanost in tehnologija trenja. Florida, ZDA: CRC Press, 2009.
3. Razmerje med sili adhezije in trenja. Isralachvili, J N, Chen, You-Lung in Yoshizawa, H. 11, 1994, Journal of Adhesion Science and Technology, Vol. 8, str. 1231-1249.
4. Zimba, J. Sila in gibanje. Baltimore, Maryland: The Johns Hopkins University Press, 2009.
5. Bhushan, b. Načela in aplikacije tribologije. New York: John Wiley in Sons, 1999.
6. Sharma, c s in purohit, k. Teorija mehanizmov in strojev. New Delhi: Prentice Hall of India, 2006.