Dinamični ali kinetični koeficient trenja, primeri, vaje

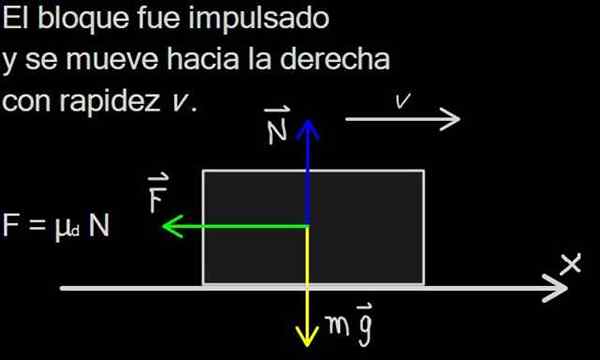
The Dinamično trenje ali kinetic To je tisti, ki se pojavi med dvema telesama v stiku, ko se površina enega od njih premakne glede na površino drugega. Na primer, v škatli, ki drsi trenje na pobočju, je dinamično in razporejeno na kontaktni površini bloka.

Naklon mora biti dovolj velik, tako da je tangencialna sestavina teže enaka ali premaga silo trenja, sicer bi se blok, ki se spusti.

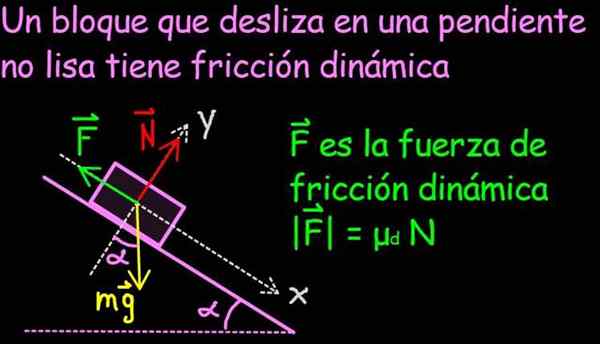Slika 1. Sila trenja je razporejena na kontaktni površini bloka, v diagramu sil pa je predstavljena kot ena sama sila F, vir: F. Zapata

Sila trenja je izjemno pomembna v vsakdanjem življenju, saj omogoča gibanje ljudi, živali in vozil. Na površini brez trenja, kot je sladoled, ni mogoče začeti gibanja.

Trenje omogoča tudi, da se naši avtomobili ustavijo, ko se premikajo.

Pri nanašanju zavor se zavorne ploščice zategnejo na kolesne diske in zahvaljujoč dinamičnemu trenju, ustavite njihovo vrtenje. Vendar ni dovolj, da bi imeli dobre zavore, potrebno je, da je med pnevmatikami in tlemi dovolj moči trenja, ker je končno to sila, od katere smo odvisni, tako da se avto ustavi.

Človeštvo se je naučilo ravnati s trenjem v svojo korist. Tako se je začelo z uporabo trenja med dvema kosoma suhega lesa za ogenj.

Narava se je naučila tudi obvladati trenje v svojo korist. Na primer, sinovialne membrane, ki pokrivajo kosti sklepov, so ena izmed površin z najnižjim koeficientom trenja, ki obstaja.

[TOC]

Dinamični koeficient trenja

Prvi, ki je sistematično preučeval gibanje bloka, ki drsi na ravni površini, je bil Leonardo da Vinci, vendar so njegove študije ostale neopažene.

Vam lahko služi: Dirac Jordan Atomski model: značilnosti in postulati

Šele v sedemnajstem stoletju je francoski fizik Guillaume Amontons ponovno odkril zakone trenja:

Dinamični zakoni o trenju

1.- Sila trenja, ki je prisotna v bloku, ki drsi na ravni površini, vedno nasprotuje smeri gibanja.

2.- Obseg dinamične sile trenja je sorazmerna z normalno tesnostjo ali silo med površinami bloka in podporno ravnino.

3.- Proporcionalna konstanta je koeficient trenja, statični μ_in V primeru, da nimate zdrsa in dinamičnega μ_d Ko je. Koeficient trenja je odvisen od materialov površin v stiku in stanja hrapavosti.

4.- Sila trenja je neodvisna od navideznega kontaktnega območja.

5.- Ko se gibanje ene površine začne glede na drugo, je sila trenja konstantna in ni odvisna od relativne hitrosti med površinami.

V tem primeru ni drsnega, statično trenje se uporablja, katere sila je manjša ali enaka statičnemu koeficientu trenja, pomnoženo z normalno.

Slika 2. Dinamična sila trenja nasprotuje smeri gibanja in njena velikost je sorazmerna s normalno silo. Konstanta sorazmernosti je dinamični koeficient trenja. Vir: f. Zapata.

Zadnja nepremičnina je bila rezultat prispevka francoskega fizika Charlesa Augustina iz Couloma, bolj znanega po svojem znanem zakonu sile med specifičnimi električnimi obtožbami.

Ta opažanja nas vodijo do matematičnega modela za dinamično trenje F:

F = μ_d N

Kjer μ_d To je dinamični koeficient trenja in N je običajna sila.

Kako določiti koeficient dinamičnega trenja?

Dinamični koeficient trenja med dvema površinama se določi eksperimentalno. Njegova vrednost ni odvisna le od materialov na obeh površinah, ampak od hrapavosti ali poliranja, ki ga imajo, pa tudi njene čistoče.

Vam lahko služi: mehanski valovi: značilnosti, lastnosti, formule, vrste

Eden od načinov, kako ga določiti, je povečati in drsniti znano škatlo na vodoravni površini.

Če je hitrost znana v času vožnje in razdalja, ki jo prevozimo od tega časa.

Poskus 

V tem poskusu se meri začetna hitrost v in razdaljo d, Torej je zavorni pospešek:

A = - v² / 2D

Diagram sil je prikazan na sliki 2. Obseg teže je masa m bloka, pomnožena s pospeševanjem gravitacije G, in kot je znano, teža vedno kaže navpično navzdol.

N To je normalna sila zaradi potiska podporne površine in je vedno pravokotna (ali normalna) do ravnine. Običajno obstaja, medtem ko so površine v stiku in prenehajo takoj, ko se površine ločijo.

Moč F predstavlja dinamično silo trenja. Dejansko je razporejen na spodnji površini bloka, vendar ga lahko predstavljamo kot eno samo silo F Uporablja se na sredini bloka.

Ker obstaja navpično ravnovesje, velikost običajnega N Je enak teži mg:

N = mg

V horizontalni smeri sile trenja povzroči upočasnitev masnega bloka M po Newtonovem drugem zakonu:

-F = m a

Trenje F kaže na levo, zato je njegova vodoravna komponenta negativna, m je masa bloka in a je zavorni pospešek.

Prej pridobljen A = - v² / 2D In tudi dinamični model trenja kaže, da:

F = μD n

Zamenjava v prejšnji enačbi imate:

-μ_d N = - v² / 2D

Ob upoštevanju, da je n = mg, lahko že počistite koeficient dinamičnega trenja: 

Vam lahko služi: Schrödinger atomski model

μ_d = v² / (2d mg)

Tabela koeficienta rocy nekaterih materialov

Naslednja tabela prikazuje statične in dinamične koeficiente trenja za različne materiale. Treba je opozoriti, da je sistematično statični koeficient trenja vedno večji od koeficienta dinamičnega trenja.

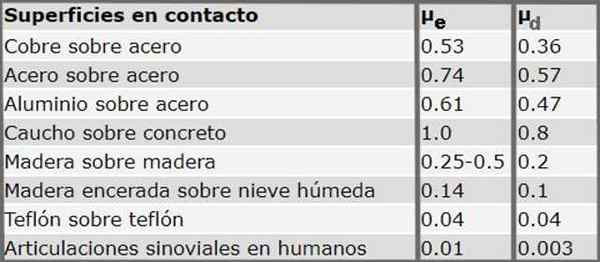Slika 3. Statični in dinamični koeficienti trenja za več površin v stiku. Vir: Serway R.Do. Fizično. McGraw-Hill (1992)

Vaje

- Vaja 1

Promovira 2 kg blok testa na vodoravnem tleh in se sprosti. V času izida se zabeleži hitrost 1,5 m/s. Od tega trenutka, dokler se blok ne ustavi z dinamičnim trenjem 3 m. Določite koeficient kinetičnega trenja.

Rešitev

Glede na formulo, pridobljeno v primeru prejšnjega odseka, je dinamičen (ali kinetični) koeficient:

μ_d = v² / (2d mg) = 1.52 / (2x3x2 x9.8) = 0,019.

- Vaja 2

Če vemo, da se blok na sliki 1 spušča s konstantno hitrostjo, da je masa bloka 1 kg in da je naklon ravnine 30 °, določa:

a) Vrednost dinamičnega trenja

b) koeficient dinamičnega trenja med blokom in ravnino.

Rešitev

Na sliki 4 je prikazana enačba gibanja (drugi zakon Newtona) za problem bloka, ki se spusti naklon s koeficientom trenja μ_d  in α naklon (glej diagram sil na sliki 1)

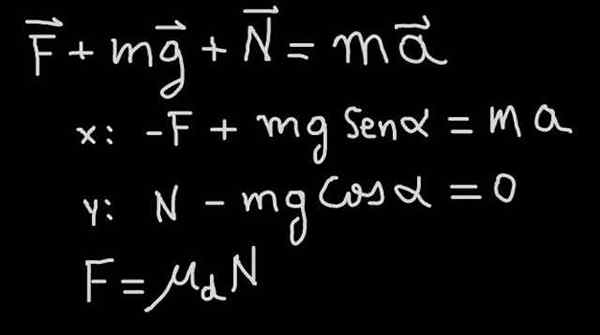Slika 4. Newtonov drugi zakon je veljal za blok, ki drsi na pobočju s trenjem. Vir: f. Zapata.

V naši vadbi nam rečejo, da se blok spušča s konstantno hitrostjo, zato se s pospeševanjem spušča. Od tam sledi, da je sila trenja takšna, da je enaka tangencialni komponenti teže: f = mg sen (α).

V našem primeru m = 1 kg in α = 30 °, tako da ima trenje F vrednost 4,9n.

Po drugi strani je normalna sila n enaka in v nasprotju s pravokotno komponento teže: n = mg cos (α) = 8,48n .

Od tam sledi, da je koeficient dinamičnega trenja:

μ_d = F / n = 4,9n / 8,48n = 0,57

Reference

1. Alonso m., Finn e. 1970. Fizično. Zvezek I. Mehanika. Interameriški izobraževalni sklad s.Do.
2. Bauer, w. 2011. Fizika za inženiring in znanosti. Zvezek 1. MC Graw Hill.
3. Hewitt, str. 2012. Konceptualna fizikalna znanost. Peta izdaja.
4. Rex, a. 2011. Osnove fizike. Pearson. 
5. Serway r. 1992. Fizično. McGraw-Hill.
6. Mladi, h. 2015. Univerzitetna fizika s sodobno fiziko. 14. izd. Pearson.