Fizično

Značilnosti in primeri elipsoidov

Značilnosti in primeri elipsoidov

On elipsoid To je površina v prostoru, ki spada v skupino štirikolesnih površin in katerih splošna enačba je v obliki:

Sekira2 + Mimo2 + Cz2 + Dxy + exz + fyz + gx + hy + iz + j = 0

To je tridimenzionalni ekvivalent elipse, za katerega je značilno eliptične in krožne sledi v nekaterih posebnih primerih. Sledi so krivulje, ki jih dobimo pri sekanju elipsoida z ravnino.

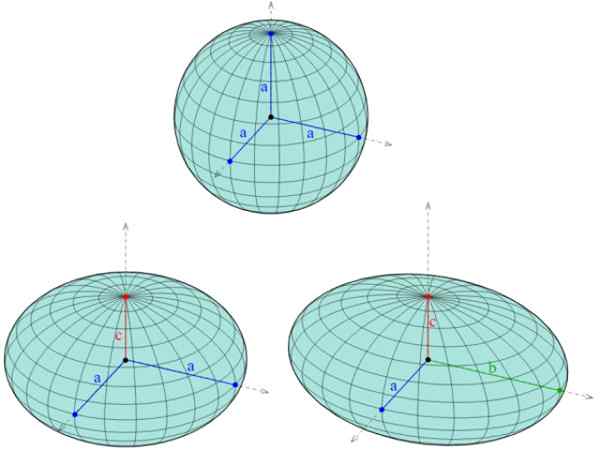
Slika 1. Trije različni elipsoidi: nad kroglo, v kateri so trije polsemi enaki, navzdol na levi sferoid, z dvema enakima pol -enim osi in na koncu navzdol v desno, triasni sferoid, s tremi osi različne dolžine. Vir: Wikimedia Commons. Ag2gaeh/cc by-s (https: // creativeCommons.Org/licence/by-sa/4.0

Poleg elipsoida obstaja pet drugih kvadratnih: hiperboloid enega lista in dveh listov, dve vrsti paraboloidov (hiperbolični in eliptični) in eliptični stožec. Tudi njegovi sledi so stožčasti.

Elipsoid se lahko izrazi tudi s standardno enačbo v kartezijanskih koordinatah. Elipsoid, osredotočen na izvor (0,0,0) in je izražen na ta način, spominja na elipse, vendar z dodatnim izrazom:

Vrednosti do, b in c So realne številke, večje od 0 in predstavljajo tri elipsoidne polovice.

[TOC]

Značilnosti elipsoidov

- Standardna enačba 

Standardna enačba v kartezijanski koordinatah za elipse se je osredotočila na točko (H, K, M) je:

- Parametrične enačbe elipsoidov

V sferičnih koordinatah lahko elipsoid opišemo na naslednji način:

x = greh θ. cos φ

y = b sin θ. greh φ

Z = c cos θ

Elipsoidni pol -out so še vedno A, B in C, parametri pa sta kota θ in φ naslednje slike:

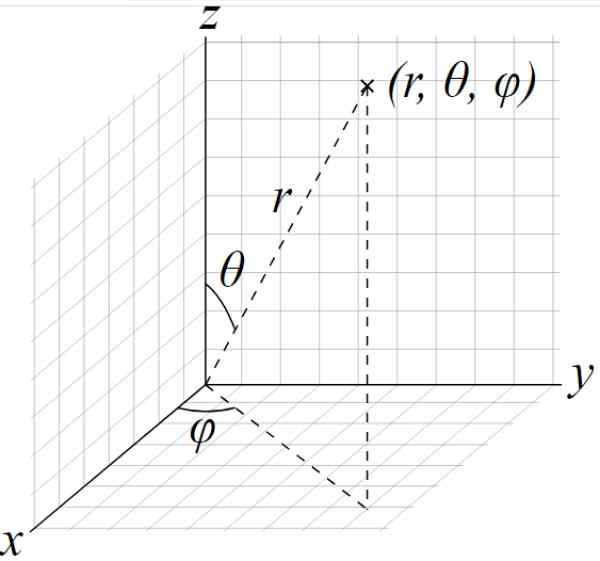Slika 2. Sferični koordinatni sistem. Elipsoid lahko parametriziramo z uporabo kotov, prikazanih kot parametri. Vir: Wikimedia Commons. Andeggs / pub domena.

- Elipsoidni sledi

Splošna enačba površine v prostoru je f (x, y, z) = 0 in sledi površine so krivulje:

Vam lahko služi: vektorska velikost

- x = c; F (c, y, z) = 0

- y = c; F (x, c, z) = 0

- Z = c; F (x, y, c) = 0

V primeru elipsoida so takšne krivulje elipse in včasih okolice.

- Glasnost

Prostornina V elipsoida je podana z (4/3) π krat večjo produkt njegovih treh polsemijev:

V = (4/3) π. ABC

Posebni elipsoidni primeri

-Elipsoid postane krogla, ko so vsa polovica velikosti enaka velikosti: a = b = c ≠ 0. To je smiselno, saj je elipsoid kot krogla, v kateri se je v vsaki osi raztezala drugače.

-Sferoid je elipsoid, v katerem sta dva polje enaka, tretji.

Sferoid se imenuje tudi revolucijski elipsoid, ker ga lahko ustvarimo z vrtenjem elips okoli osi.

Če osi zavoja sovpada z glavno os, je sferoid razširitev, Če pa sovpada z manjšo osi oblat:

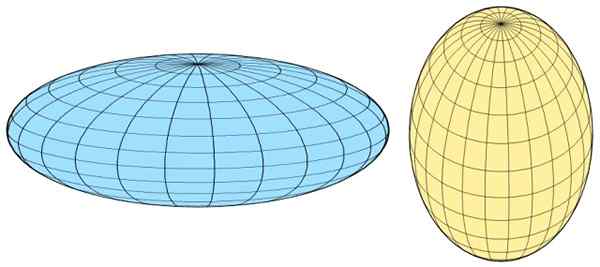Slika 3. Sferoid levo na levo in širjenje sferoida na desno. Vir: Wikimedia Commons.

Ukrep sploščenja sferoida (eliptičnosti) je podana z razlika v dolžini med obema polstranskima stranma, izraženo v delni obliki, torej je to enota, ki jo je dalo:

F = (a - b) / a

V tej enačbi A predstavlja pol -senije in B manjše pol -oke, ne pozabite, da je tretja os enaka kateri koli od teh za sferoid. Vrednost F je med 0 in 1, za sferoid pa mora biti večja od 0 (če bi bila enaka 0, bi preprosto imeli kroglo).

Vam lahko služi: bethelgeuse

Referenčni elipsoid

Planeti in na splošno zvezde običajno niso popolne sfere, ker se vrtenje okoli svojih osi, ki v Ekvadorju rade telo v drogovih in basinalih.

Zato se izkaže, da je zemlja kot oblatni sferoid, čeprav ni tako pretirana kot prejšnja številka, na drugi strani.

Torej bolj realističen način zastopanja planetov je domnevati, da so kot sferoid ali elipsoid revolucije, katere pol -semi -major je ekvatorialni radio in manjši pol -osi polarni polmer.

Previdni ukrepi na svetu so omogočili gradnjo Referenčni elipsoid Zemlje kot najbolj natančne oblike za matematično delo.

Zvezde imajo tudi rotacijske gibe, ki jim dajejo več ali manj sploščene oblike. Hitra zvezda Aternar, osma najsvetlejša zvezda na nočnem nebu, v južnem ozvezdju Eridanusa, je izjemno eliptična, če jo primerjamo z večino. Od nas je 144 svetlobnih let.

Na drugi skrajnosti so pred nekaj leti znanstveniki dali z najbolj sferičnim objektom do zdaj: Kepler 11145123 Star, 5000 svetlobnih let, z velikostjo, dvakrat večji od našega sonca, in razlika med polmesami le 3 km. Kot je bilo pričakovano, se tudi počasneje obrača.

Kar zadeva Zemljo, ni popoln sferoid zaradi svoje robustne površine in lokalnih variacij gravitacije. Zato je več kot en na voljo referenčni sferoid in na vsakem mestu je izbrano najprimernejše lokalne geografije.

Lahko vam služi: kakšna je dolina v fiziki? (S primeri)

Pomoč satelitov je neprecenljiva pri ustvarjanju vse bolj natančnih modelov zemlje.

Slika 4. Haumea, transneptunski pritlikavi planet ima elipsoidno obliko. Vir: Wikimedia Commons.

Številčni primer

Zaradi vrtenja zemlje je nastala centrifugalna sila, ki ji daje obliko podolgovatega elipsoida, namesto s krogle. Znano je, da je ekvatorialni radio Zemlje 3963 milj, polarni polmer pa 3942 milj.

Poiščite enačbo ekvatorialne sledi, enačbe tega elipsoida in ukrep njenega sploščenja. Primerjajte tudi s Saturnovo eliptičnostjo s spodaj navedenimi podatki:

-Saturn ekvatorialni radio: 60268 km

-Saturn Polar Radio: 54364 km

Rešitev

Potreben je koordinatni sistem, za katerega bomo domnevali, da se osredotoči na izvor (središče zemlje). Domnevali bomo, da je navpična os Z in sled, ki ustreza ekvatorju, na ravnini XY, kar ustreza ravnini z = 0.

V ekvatorialni ravnini sta pol -a in B enaka, torej a = b = 3963 milj, c = 3942 milj. To je poseben primer: sferoid, osredotočen na točko (0,0,0), kot je navedeno zgoraj.

Ekvatorialna sled je krog polmera r = 3963 milj, osredotočen na izvor. Izračuna se z z = 0 v standardni enačbi:


In standardna enačba zemeljskega elipsoida je:

Končno se izračuna ukrep prilagoditve (eliptični) v enačbi:

F Zemlja = (a - b) / a = (3963-3942) milje / 3963 milj = 0.0053

F Saturn = (60268-54363) km/60268 km = 0.0980

Upoštevajte, da je eliptična F brezdimenzionalna količina.

Reference

  1. Arcgis za namizje. Sferoid in kroglice. Obnovi se od: namizje.Arcgis.com.
  2. BBC svet. Skrivnost najbolj sferičnega predmeta, ki so ga kdaj odkrili v vesolju. Pridobljeno iz: BBC.com.
  3. Larson, r. Izračun in analitična geometrija. Šesta izdaja. Zvezek 2. McGraw Hill.
  4. Wikipedija. Elipsooid. Pridobljeno iz: v.Wikipedija.org.
  5. Wikipedija. Siperoid. Pridobljeno iz: v.Wikipedija.org.