Stisljivost trdnih snovi, tekočin, plinov, primeri

The stisljivost snovi ali materiala je sprememba volumna, ki jo doživlja, ko je podvržena sprememba tlaka. Običajno se glasnost zmanjšuje, ko pritiskate na sistem ali predmet. Vendar se včasih zgodi nasprotno: sprememba tlaka lahko povzroči eksplozijo, v kateri sistem poveča prostornino ali ko pride do spremembe faze.

V nekaterih kemičnih reakcijah se to lahko zgodi in tudi v plini, saj s povečanjem pogostosti trkov potekajo odbojne sile.

Podmornica doživi stiskalne sile, ko je potopljena. Vir: Pixabay.com.

Če si predstavljate, kako enostavno ali težko je stisniti predmet, morate upoštevati tri stanja, v katerih je zadeva običajno: trdna, tekočina in plinasta. V vsakem od njih molekule držijo določene razdalje drug od drugega. Bolj trdne so povezave, ki združujejo molekule snovi, ki sestavljajo predmet in bližje, težje bo povzročiti deformacijo.

Trdna snov ima svoje zelo tesne molekule, in ko preizkušajo več, se pojavijo odbojne sile, ki ovirajo nalogo. Zato je rečeno, da so trdne snovi nekompresivne. V tekočih molekulah je več prostora, zato je njegova stisljivost večja, vendar še vedno sprememba volumna običajno zahteva velike sile.

Torej trdne snovi in ​​tekočine težko stisnejo. Zelo velika sprememba tlaka bi bila potrebna, da bi dosegli opazno spremembo tako imenovanega normalnega tlaka in temperaturnih pogojev. Po drugi strani se plini, saj imajo zelo razmaknjene molekule, zlahka stisnejo in dekompresirani.

[TOC]

Trdna stisljivost

Ko je na primer predmet potopljen v tekočino, izvaja pritisk na predmet v vse smeri. Na ta način si lahko mislimo, da se bo obseg predmeta zmanjšal, čeprav v večini primerov to ne bo opazno.

Situacija je razvidna na naslednji sliki:

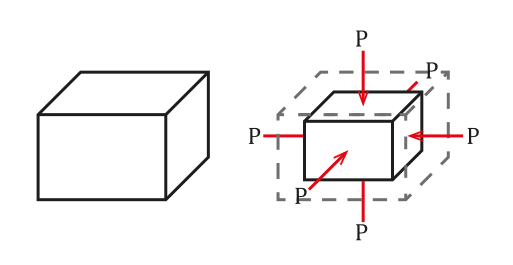Sila, ki jo izvaja tekočina na potopljenem predmetu, je pravokotna na površino. Vir: Wikimedia Commons.

Tlak je opredeljen kot sila na enoto, kar bo povzročilo spremembo volumna ΔV, sorazmerno z začetnim prostornino predmeta V_tudi. Ta sprememba zvezka bo odvisna od lastnosti istega.

Hookejev zakon navaja, da je deformacija, ki jo doživlja predmet, sorazmerna s trudom, ki se uporablja zanj:

Napor ∝ deformacija

Volumetrična deformacija, ki jo doživlja telo Volumetrični modul materiala:

B = -seft/enotna deformacija

Vam lahko služi: toplotno sevanje: lastnosti, primeri, aplikacije

B = -Δp/ (ΔV/ V_tudi)

Kot ΔV/V_tudi To je brezdimenzionalna količina, saj je količnik med dvema zvezkama, volumetrični modul ima enake tlačne enote, ki so v mednarodnem sistemu Pascal (PA).

Negativni znak kaže na pričakovano zmanjšanje volumna, ko je predmet dovolj stisnjen, to je, da se tlak poveča.

-Stisljivost materiala

Inverzna ali vzajemna vrednost volumetričnega modula je znana kot stisljivost In označena je z besedilom k. Zato:

Tukaj k Je negativna sprememba frakcijske volumne zaradi povečanja tlaka. Njegove enote v mednarodnem sistemu so inverzne od PA, to je m² /N.

Enačba za B ali K, če je prednostna, je uporabna za trdne snovi in ​​tekočine. Koncept volumetričnega modula se redko uporablja za pline. Kasneje je razložen preprost model, ki količinsko določi zmanjšanje prostornine, ki ga lahko doživi resnični plin.

Hitrost zvoka in modul stisljivosti

Zanimiva aplikacija je hitrost zvoka v mediju, ki je odvisna od modula stisljivosti istega:

Kjer je C hitrost zvoka, je B volumetrični modul in ρ gostota medija

Rešene vaje-primere

-Vaja rešena 1

Trdna medeninasta krogla, katere prostornina je 0.8 m³ Pade v ocean do globine, v kateri je hidrostatični tlak 20 m večji kot na površini. Kakšna sprememba bo doživela glasnost sfere? Znano je, da je modul medeninaste stisljivosti B = 35 000 MPA,

Rešitev

1 m pa = 1 mega pascal = 1. 10 ⁶ Pa

Sprememba tlaka glede na površino je dp = 20 x 10 ⁶ Pa. Z uporabo dane enačbe za B imate:

B = -Δp/ (ΔV/ V_tudi)

Zato:

Tako:

ΔV = -5.71.10 ^-4 x 0.8 m³ = -4.57 x 10^-4 m³

Razlika v glasnosti ima lahko negativen znak, ko je končni glasnost manjši od začetnega obsega, zato se ta rezultat strinja z vsemi predpostavkami, ki smo jih dosegli do zdaj.

Tako visok modul stisljivosti kaže, da je potrebna velika sprememba tlaka, tako da objekt doživi opazno zmanjšanje volumna.

-Vaja Rešena 2

Če se v daljavo približuje uho proti železniškemu tiru. Kako dolgo traja zvok, ko potujete skozi jekleno tirnico, če je vlak oddaljen 1 km?

Vam lahko služi: ohranjanje linearnega zagona: načelo, primeri, vaje.

Podatki

Jeklena gostota = 7.8 x 10 ³ kg/m3

Modul za stisljivost jekla = 2.0 x 10 ^enajst Pa.

Rešitev

Stisljivost tekočin

Zgoraj izračunan modul za stisljivost se uporablja tudi za tekočine, čeprav je za znatno zmanjšanje volumna običajno potreben velik napor. Toda tekočine se lahko širijo ali se krčijo, ko se segrejejo ali ohladijo, in tudi, če se ne odvračajo ali pritiskajo.

Za vodo v standardnih tlačnih in temperaturnih pogojih (0 ° C in tlačno atmosfero približno ali 100 kPa) je volumetrični modul 2100 MPa. To pomeni približno 21000 -krat atmosferski pritisk.

Zato se v večini aplikacij tekočine običajno štejejo za nestisljive. To je mogoče takoj videti s numerično uporabo.

-Vaja rešena 3

Poiščite delno zmanjšanje volumna vode, če je podvrženo tlaku 15 MPa.

Rešitev

Stisljivost v plinih

Plini, kot je razloženo zgoraj, delujejo nekoliko drugače.

Vedeti, kakšno glasnost imajo n moli določenega plina, ko je pritisnjen Str in pri temperaturi T, Uporablja se državna enačba. V državni enačbi za idealen plin, kjer medmolekularne sile niso upoštevane, najpreprostejši model kaže, da:

Str.V_idealno = n. R. T

Kjer je r konstanta idealnih plinov.

Spremembe volumna plina se lahko izvedejo pri konstantnem tlaku ali pri konstantni temperaturi. Na primer, z ohranjanjem temperaturne konstante, izotermalna stisljivost κ_T je:

Namesto simbola "delta", ki je bil uporabljen pred določitvijo koncepta za trdne snovi, za plin je opisan z derivatom, v tem primeru delno izpeljan glede na P, ohranjanje konstantne t.

Zato B_T Izotermalni modul stisljivosti je:

 B_T = p

Pomemben je tudi adiabatski modul B -Compresibilnosti B_adiabatski, Za katerega ni dohodnega ali odhodnega toplotnega toka.

B_adiabatski = γP

Kjer je γ adiabatski koeficient. S tem koeficientom lahko izračunate hitrost zvoka v zraku:

-Vaja rešena 4

Če uporabite prejšnjo enačbo, poiščite hitrost zvoka v zraku.

Podatki

Adiabatski modul stisljivosti zraka je 1,42 × 10⁵ Pa

Gostota zraka je 1.225 kg/m³ (pri atmosferskem tlaku in 15 ° C)

Rešitev

Faktor stisljivosti z

Namesto da bi delali z modulom stisljivosti, kot enotna sprememba volumna zaradi spremembe tlaka, Faktor stisljivosti pravega plina, Drugačen, a ilustrativni koncept o tem, kako se resnični plin primerja z idealnim plinom:

Vam lahko služi: valovita teorija svetlobe: razlaga, aplikacije, primeri

Str . V_Resnično = Z. R. T

Kadar je Z konsibilnost stisljivosti plina, ki je odvisna od pogojev, pod katerimi je, je običajno funkcija p in temperaturnega tlaka T, ki se lahko izrazi kot:

Z = f (p, t)

V primeru idealnega plina z = 1. Za realne pline se vrednost z s pritiskom skoraj vedno poveča in se s temperaturo zmanjšuje.

S povečanjem pritiska se plinaste molekule pogosteje trčijo in odbojne sile med njimi se povečajo. To lahko privede do povečanja obsega v realnem plinu, zato z> 1.

Po drugi strani se molekule lahko premikajo in prevladujejo sile privlačnosti. V tem primeru z < 1.

Za preprost primer 1 mol plina n = 1, če se ohranijo enaki tlačni in temperaturni pogoji, z delitvijo izraza dobimo prejšnje enačbe:

Sklenjeno je, da:

V_Resnično = Z v_idealno

-Vaja rešena 5

Obstaja pravi plin pri 250 ° K in 15 atm tlaka, ki ima molsko prostornino 12 % nižji od tistega, ki ga izračuna status idealnih plinov. Če tlak in temperatura ostaneta konstantna, poiščite:

a) Faktor stisljivosti.

b) molarna prostornina resničnega plina.

c) Kakšne sile prevladujejo: privlačne ali odbojne?

Rešitev

a) Če je resnična glasnost 12 % nižja od ideala, to pomeni, da:

V_Resnično = 0.88 V_idealno

Zato je za 1 mol plina faktor stisljivosti:

Z = 0.88

b) Izbira konstante idealnih plinov z ustreznimi enotami za predložene podatke:

R = 0,082 l.bankomat/mol.K

Molarni volumen se izračuna z čiščenjem in nadomeščanjem vrednosti:

c) Prevladujejo privlačne sile, saj je z manjši od 1.

Reference

1. Atkins, str. 2008. Fizikalna kemija. Pan -american Medical uredništvo. 10 - 15.
2. Giancoli, d.  2006. Fizika: načela z aplikacijami. 6^th. Ed Prentice Hall. 242 - 243 in 314-15
3. Mott, r.  2006. Mehanika tekočine. Pearson Education.13-14.
4. Rex, a. 2011. Osnove fizike. Pearson Education. 242-243.
5. Tipler, str. (2006) Fizika za znanost in tehnologijo. 5. izd. Zvezek 1. Uredništvo se je vrtelo. 542.