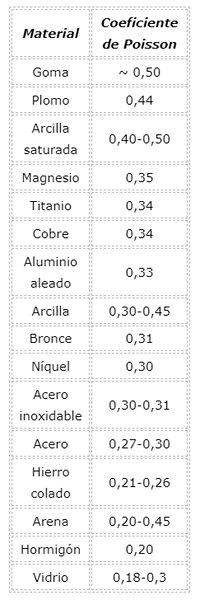
Poissonov koeficient koeficienta, formule, vrednosti, primeri
- 4453
- 100
- Adrian Legros
On Poissonov koeficient Je brezdimenzionalna količina, značilna za vsak material. To je pokazatelj deformacije kosa materiala pred uporabo določenih prizadevanj.
Ko materialni kos, ki se podvrže napetosti ali stiskanju, trpi deformacijo, je količnik med prečno deformacijo in vzdolžno deformacijo natančno Poissonov koeficient.
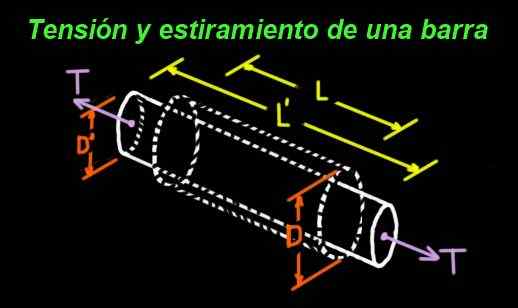
 Slika 1. Poissonov koeficient meri razmerje med vzdolžnim raztezanjem in prečnim zoženjem. (Pripravil Ricardo Pérez)
Slika 1. Poissonov koeficient meri razmerje med vzdolžnim raztezanjem in prečnim zoženjem. (Pripravil Ricardo Pérez) Na primer, gumijasti cilinder, ki je pod napetostjo na njegovih koncih, je raztegnjen v vzdolžni smeri, vendar je prečno ozka. Slika 1 prikazuje vrstico, katere izvirne dimenzije so: Long L in premer D.
Palica je podvržena t napetosti na njegovih koncih, zato zaradi te napetosti trpi raztezanje, tako da je nova dolžina l '> l. Toda pri raztezanju se na novo vrednost pojavi tudi zoženje njegovega premera: D ' < D.
Količnik med raztezanjem (pozitivno) in zoženjem (negativno), pomnoženo z (-1), je pozitivno število med 0 in 0,5. Ta številka je tako imenovani koeficient Poisson ν (grško pismo).
[TOC]
Poissonova formula koeficienta
Za izračun Poissonovega koeficienta je potrebno določiti vzdolžno in prečno enoto deformacije.
Deformacija vzdolžne enote εL To je razteg, razdeljen med prvotno dolžino:
εL = (L ' - l) / l
Podobno je prečna enotna deformacija εT To je radialno zoženje, razdeljeno med prvotnim premerom:
εT = (D ' - d) / d
Zato se Poissonov koeficient izračuna z naslednjo formulo:
ν = - εT / εL
Odnos z modulom elastičnosti in modulom togosti
Poisson ν koeficient je povezan z modulom In elastičnosti (ali mladega modula) in z modulom togosti G, po naslednji formuli:
Vam lahko služi: geometrijska optika: katere študije, zakoni, aplikacije, vajeν = e /(2g) - 1
Poissonova vrednost koeficienta za materiale
 Slika 2. Nerjavno jeklo ima Poissonov koeficient med 0,30 in 0,31. Vir: Pixabay.
Slika 2. Nerjavno jeklo ima Poissonov koeficient med 0,30 in 0,31. Vir: Pixabay. Primeri izračuna
Primer 1
Bar z določenim plastičnim materialom ima dolžino 150 mm in krožni del premera 20 mm. Ko je stiskalna sila 612,25 kg-F podvržena kompresijski sili, opazimo skrajšanje 14 mm in hkrati povečanje za 0,85 mm v premeru palice.
Izračunati:
a) vzdolžna enotna deformacija.
b) prečna enotna deformacija.
c) Poissonov koeficient tega gradiva.
d) mladičev modul elastičnosti, ki ustreza materialu.
e) modul togosti za to plastiko.
Rešitev
Spomnimo se, da je deformacija vzdolžne enote εl raztežaj, deljen s prvotno dolžino:
εl = (l ' - l) / l
εl = (-14 mm) / 150 mm = -0.0933
Upoštevajte, da je vzdolžna enotna deformacija brezdimenzionalna in v tem primeru je dala negativno, ker je prišlo do zmanjšanja njegove vzdolžne dimenzije.
Rešitev b
Podobno je enotna prečna deformacija εt radialno zoženje, deljeno s prvotnim premerom:
εt = (d ' - d) / d
εt = (+0,85 mm) / 20 mm = 0,0425
Prečna enotna deformacija je bila pozitivna, ker je prišlo do povečanja premera palice.
Rešitev c
Za izračun Poissonovega koeficienta se moramo spomniti, da je opredeljen kot negativni količnik med prečno deformacijo in vzdolžno deformacijo:
ν = - εt / εl
ν = - 0,0425 / (-0,0933) = 0,4554
Ne pozabite, da je Poissonov koeficient pozitivno brezdimenzionalno število, za večino materialov pa je med 0 in 0,5.
Vam lahko služi: Darcy LawRešitev d
Young's Elastity Modul, označen s črko E, je sorazmernost v Hookejevem zakonu. Skozi E je normalen napor σl povezan z enotno deformacijo εL, kot sledi:
σl = e εl
Običajni napor je opredeljen kot količnik med normalno silo (v tem primeru vzporedno z osi palice) in presekom:
σl = f / a = f / (π / 4 * d^2)
V tej vaji je sila F 612,25 kg-f, kar bo narejeno Newtonsu, kar je enota sile:
F = 612,25 kg-f = 612,25 * 9,8 n = 6000 n = 6 kn
Prerez A je s svojim delom:
A = (π/4 * d^2) = (3,1416/4) * (20 * 10^-3 m)^2 = 3,1416 * 10^-4 M^2
Končno je običajni napor, ki se uporablja za bar,:
σl = f / a = 6000 n / 3,1416 * 10^-4 m^2 = 19.098.593 PA = 19.098 MPA
Za izračun modula za elastičnost Young smo očiščeni in Hookeovega zakona σl = e εl:
E = σl / εl = 19.098.593 PA / 0,0933 = 204,7 MPA
Rešitev e
Modul R togosti je povezan z Youngovim EG modulom in Poisson ν koeficient s to formulo:
E / (2 g) = 1 + ν
Od tam lahko očistite G:
G = e / (2 (1 + ν)) = 204,7 MPA / (2 (1 + 0,4554)) = 70,33 MPA
Primer 2
Imate kabel 4 mm in 1 m dolg premer. Ker ve, da je bakreni mladi modul 110000 MPa in da je njegov Poissonov koeficient 0,34, ocenjuje, da se razteza in zoži v premeru.
Rešitev
V prvi vrsti je treba izračunati normalno vlečno naporo, ki ga teža izvaja na žici po tej formuli:
Vam lahko služi: vektorji v vesolju: kako graditi, aplikacije, vajeσl = f / a = f / (π / 4 * d^2)
Sila F je 980 N, presek pa je:
A = (π/4 * d^2) = (3,1416/4) * (4 * 10^-3 m)^2 = 1.2566 * 10^-5 M^2
Potem je vlečni napor:
σl = 980 n / 1,2566 * 10^-5 m^2 = 77.986.000 Pa
Izračun enotne deformacije žice
Young's Elastity Modul, označen s črko E, je konstanta sorazmernosti v Hookejevem zakonu, ki se nanaša na normalen napor σl z enotno deformacijo εl:
σl = e εl
Od tam se lahko odstrani vzdolžna enotna deformacija bakrene žice:
εl = σl / e = 77,986 MPA / 110000 MPA = 7,09 * 10^-4
Izračun prečne enotne deformacije
Po drugi strani se za poznavanje prečne enotne deformacije uporablja Poissonov koeficient:
ν = - εt / εl
Končno morate prehodno enotno deformacijo:
εt = -ν εl = -0,34 * 7,09 * 10 ^-4 = -2,41 * 10 ^-4
Kabel Absolutni izračun raztezanja
Končno, da poznamo absolutno raztezanje kabla, je treba uporabiti naslednje razmerje:
ΔL = εl * l = 7,09 * 10^-4 * 1 m = 7,09 * 10^-4 m = 0,709 mm
Torej s to težo se je kabel komaj raztegnil 0,709 milimetrov.
Izračun zmanjšanja premera
Za pridobitev absolutnega krčenja v premeru uporabljamo naslednjo formulo:
Δd = εt * d = -2,41 * 10 ^-4 * 4 mm = -9,64 * 10 ^-4 mm = -0.000964 milimetrov.
Ta zoženje premera je tako majhno, da ga je težko ceniti s prostim očesom, tudi njegovo merjenje zahteva visoko natančnosti instrument.
Reference
- Pivo f ... Mehanika materiala. 5. Izdaja. 2010. MC Graw Hill. 1-130.
- Hibbeler R. Mehanika materialov. Osma izdaja. Dvorana Prentice. 2011. 3-60.
- Gere J. Mehanika materialov. Osma izdaja. Cengage učenje. 4-220.
- Giancoli, d. 2006. Fizika: načela z aplikacijami. 6. izd. Dvorana Prentice. 238-242.
- Valera Negrete, J. 2005. Splošne zapise o fiziki. Ne. 87-98.