Je poklican Pomembno število na količino števk, ki vsebuje Mantisa številke. Več številk je količina znana z največjo natančnostjo. Kot opomnik je Mantisa številka, ki spremlja moč 10, ko je napisano število v znanstvenem zapisu.

Na primer, vzemimo številko 0.00376, ki je napisan kot 3.76 x 10 ^-3. Mantisa je 3.76 in število ima skupno 3 pomembne številke. Številka 0.129 ima tudi 3 pomembne številke, 4.5 ima samo 2.

Slika 1. Znanstveni kalkulatorji nikoli ne kažejo števila pomembnih številk operacije. Vir: Piqsels.

In kaj se zgodi, ko je številka celota? To pomeni, da je znana z vsemi možnimi natančnostjo, z drugimi besedami, ima neskončno natančnost. Na primer, s štetjem ljudi, živali ali predmetov, kot so knjige in telefoni, je rezultat celo število in natančno število.

Če rečemo, da je v kinu 110 ljudi, ki gledajo film, to je natančno število, niti več niti manj in ima 3 pomembne številke.

Pomembne številke obravnavajo nekatera preprosta pravila, ki jih zapomnimo z malo prakse, kot bomo videli.

[TOC]

Pravila za določitev pomembnih številk

Pravilo 1

Prejšnje ničle ne štejejo za pomembno številko, torej 0.045 in 4.5 imata obe pomembni številki, saj se začneta šteti z leve strani in iz prve različne številke nič.

Pravilo 2

Zadnje ničle (na desni) do prve pomembne številke štejejo za pomembno številko (če je upravičena z natančnostjo merilnega instrumenta).

Nazadnje so tudi ničle, ki so na sredini.

Pravilo 3

Za številke, napisane v znanstvenem zapisu, so vse številke Mantisa pomembne in eksponent ne vpliva na natančnost.

Lahko vam služi: povprečna hitrost: formule, kako se izračuna in reši

Pravilo 4

Ko se operacije z decimali izvajajo, na primer z izračunom območij ali drugih podobnih operacij, mora imeti rezultat enako število pomembnih številk kot znesek z najnižjim številom pomembnih številk, ki so sodelovali pri operaciji. To pravilo velja za vsako aritmetično delovanje.

Pravilo 5

Število števila ne vpliva na njegovo število pomembnih številk.

Takoj bomo videli nekaj primerov tega in vseh drugih pravil.

Primeri

Primer 1

Poiščite, koliko pomembnih številk je v vsaki od teh številk.

a) 876

b) 1000.68

c) 0.00005026

d) 4.8

e) -6.99

Odgovori

a) 876 ima 3 pomembne številke.

b) 1000.68 ima 6 pomembnih številk, saj nič v srednjem štetju kot taki.

c) namesto 0.00005026 ima 4 pomembne številke. Upoštevajte, da se 5 ničle na levi strani 5 ne šteje za pomembna številka, namesto na 0 med 5 in 2 Da.

d) 4.8 ima 2 pomembni številki.

e) -6.99 ima 3 pomembne številke.

Primer 2

Običajno je sprejeti ukrepe, kot so metrični trakovi, ure, termometri, luske in tako na slogu. Koliko pomembnih številk moramo prijaviti zneska, ki jih merimo na ta način?

Odgovor

Odvisno je od cenitve instrumenta, s katerim se meri. Postavimo primer: izmerite zunanji premer cevi, z diplomiranim pravilom in z Vernierjem ali kraljevim stopalom.

Vernier je instrument, ki dolžine meri zelo natančno, ker ima dodatno majhno lestvico, imenovan Vernier, kar omogoča večjo finost, tako rekoč pri merjenju.

Je natančnejši od diplomiranega pravila, ker se lahko z njim naučimo pomembnejših številk določene dolžine.

Zato ni smisla poročati o obodu, recimo, 35.88 cm, če ga izmerimo z meritvijo traku, saj ta instrument ni dovolj natančen, da bi lahko poročal o toliko pomembnih številkah.

Vam lahko služi: statična: zgodovina, kakšne študije, aplikacije, zakoni

Zahvaljuje ukrep traku je podano z:

Za ukrep traku ali milimetrsko pravilo A = 1 mm, ki je desetina centimetra. Obile, izmerjen z merilnim trakom, je treba poročati kot 35.9 cm.

Primer 3

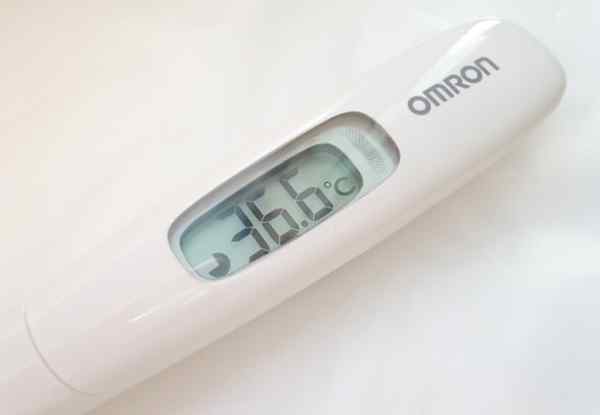
Koliko pomembnih številk ima branje z digitalnim termometrom?

Odgovor

Termometer slike ponuja odčitke temperature s tremi števki. Vendar, kolikor je prikazano, 36.6 ° C, le prva dva števka od leve proti desni sta natančna, saj na decimalko vpliva napaka pri spoštovanju instrumenta, ki je običajno navedena na zadnji strani istega ali v njegovem priročniku za operacije.

Običajna stvar za vrsto prikazanega digitalnega instrumenta je napaka pri 0.1 ° C. To je dovolj, da se prepričate, da ni vročine.

Slika 2. Digitalni termometer, katerega odčitki so 3 pomembne številke. Vir: pxhere.

Pravila za okrogle številke

Ko se kalkulator uporablja za izvajanje izračunov s pridobljenimi ukrepi, ni pravilno dati rezultata z uporabo vseh števk, ki se prikažejo na zaslonu.

Ohranijo se samo tisti, ki se natančno poznajo. Potem je treba rezultate zaokrožiti, da se natančno prilagodi številu znanih številk. Ta pravila so:

-Če je številka, ki sledi številka, ki jo je treba ohraniti enako ali večji od 5, Temu je dodana 1.

Na primer z zaokrožitvijo 3.786 Da bi imeli dve decimali, želimo obdržati številke do 8. Ker je številka, ki sledi (6), večja od 5, 8 postane 8 + 1 = 9 in številka ostane 3.79.

-Ko je številka, ki jo je treba ohraniti manj kot 5, Številka je enaka.

Vam lahko služi: Joule Effect: Pojasnilo, primeri, vaje, aplikacije

Če želimo 1. krog.27924 imeti le 3 decimalke, to dosežemo z dosegom 9, čemur sledi 2. Ker je 2 manj kot 5, ti decimali izginejo in zaobljeno število je 1.279.

Vaja rešena

Jedilna miza ima obliko in dimenzije, prikazane na priloženi sliki. Zahteva se, da svoje območje izračuna s pravili operacij s pomembnimi podatki.

Rešitev

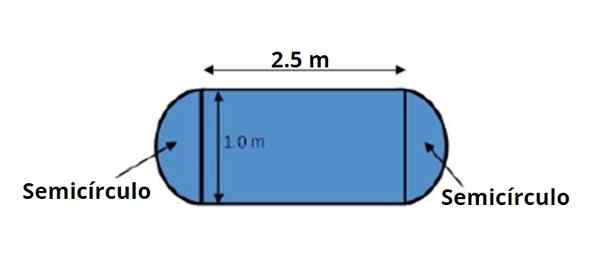Slika 3. Tabela ima obliko in dimenzije, prikazane na sliki, opazite, da sta ti znani z dvema pomembnima številkama. Vir: f. Zapata.

Območje mize lahko razdelimo na osrednje pravokotno območje in dva polkroga, po enega na vsaki strani, ki skupaj naredi 1 polni krog.

Poklicali bomo₁ na območje pravokotnika, ki ga daje:

Do₁ = osnova × višina = 2.5 m x 1.0 m = 2.5m²

Področje kroga, ki je enakovredno območju 1 polkroga, pomnoženega z 2, je:

Do₂ = π × radio²

Premer katerega koli od polkrog je 1.0 m, zato je polmer 0.50 m. Premer bi lahko uporabili tudi neposredno za izračun območja, v tem primeru:

Do₂ = (premer π ײ) / 4

V vsakem primeru:

Do₂ = [π x (1.0 m)²] / 4 = 0.785398163 m²

Uporabljene so bile vse števke, ki jih ponuja kalkulator. Zdaj dodamo k₁ že₂ Za skupno površino tabele:

A = (2.5 + 0.785398163) m² = 3.285398163 m²

Ker so dimenzije tabele znane z dvema pomembnima številkama, nima smisla izraziti rezultata z vsemi decimali, ki jih daje kalkulator, ki nikoli ne daje števila pomembnih številk rezultata.

Kar je treba storiti, je, da zaokrožimo območje, tako da ima enako število pomembnih številk kot dimenzije tabele, torej 2. Zato se poroča o končnem rezultatu tako:

A = 3.3 m²

Reference

1. Bauer, w. 2011. Fizika za inženiring in znanosti. Zvezek 1. MC Graw Hill.
2. Figueroa, d. (2005). Serija: Fizika za znanost in inženiring. Zvezek 1. Kinematika. Uredil Douglas Figueroa (USB).
3. FisicalAb. Pomembne številke in zaokroževanje. Okreval od: fisicalbab.com.
4. Giancoli, d.  2006. Fizika: načela z aplikacijami. 6. Ed Prentice Hall.
5. Sears, Zemansky. 2016. Univerzitetna fizika s sodobno fiziko. 14. Ed. Zvezek1.