Neelastični spopadi v dimenziji in primerih

The Neelastični pretresi ali neelastični trki so kratka in intenzivna interakcija med dvema predmetoma, v katerih se ohrani količina gibanja, ne pa kinetične energije, od katerih se odstotek spremeni v kakšno drugo vrsto energije.

Šoki ali trki so po naravi pogosti. Subatomski delci trčijo z zelo visokimi hitrostmi, medtem ko veliko športov in iger sestavljajo neprekinjeni trki. Tudi galaksije se lahko trčijo.

Slika 1. Trčenje testnega avtomobila. Vir: Pixabay

Pravzaprav je količina gibanja ohranjena v kakršni koli vrsti trka, dokler delci trčijo izoliran sistem. Torej v tem smislu ni problema. Zdaj imajo predmeti kinetično energijo, povezano z gibanjem. Kaj se lahko zgodi s to energijo, ko se zruši?

Notranje sile, ki se odvijajo med spopadom med predmeti. Ko je navedeno, da kinetična energija ni ohranjena, to pomeni, da se pretvori v druge vrste energije: na primer v zvočno energijo (trk naprave ima značilen zvok).

Več možnosti uporabe za kinetično energijo: toplota s trenjem in seveda neizogibna deformacija, ki jo ob trku trpijo predmeti, na primer avtomobilska telesa na zgornji sliki.

[TOC]

Primeri neelastičnih trkov 

- Dve masi plastike, ki se trčita in se srečata skupaj, se premikata kot en kos po nesreči.

- Gumijasta kroglica, ki odskoči ob steno ali tla. Kroglica se deformira, ko vpliva na površino.

Ni vsa kinetična energija pretvorjena v druge vrste energije, razen v nekaj izjemah. Predmeti lahko ostanejo z določeno količino te energije. Kasneje bomo videli, kako izračunati odstotek.

Ko so koščki, ki trkajo.

Popolnoma neelastični trki v dimenziji

Trk slike prikazuje dva predmeta različnih mas m₁ in m₂, premikanje drug na drugega s hitrostjo v_i1 in v_I2 oziroma. Vse se zgodi na horizontalnem, to je trk v dimenziji, najpreprostejši za preučevanje.

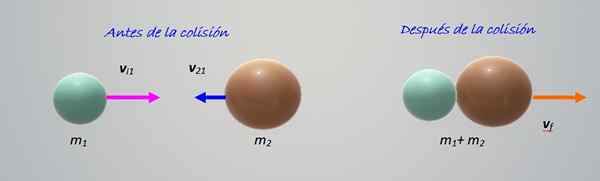Slika 2. Trčenje med dvema delcima različnih mas. Vir: Self Made.

Predmeti trčijo in se nato združijo v desno. To je popolnoma neelastično trčenje, zato je dovolj, da ohranimo količino gibanja:

Str_tudi = Str_F

Količina gibanja je vektor, katerega enote so n.s. V opisani situaciji lahko vektorski zapis izpustimo, saj gre za trke v dimenziji:

Lahko vam služi: Easy Physics Experiments (primarna univerza)

MV_tudi = MV_F

Količina gibanja sistema je vektorska vsota količine gibanja vsakega delca.

m₁ v_i1  + m₂ v_I2 = (m₁ + m₂) v_F

Končno hitrost daje:

v_F = (m₁ v_i1  + m₂ v_I2)/ (M₁ + m₂)

Koeficient vračila

Obstaja količina, ki lahko kaže, kako elastična je trčenje. To je približno Koeficient vračila, ki je opredeljen kot negativno razmerje med relativno hitrostjo delcev po nesreči in relativno hitrostjo pred nesrečo.

Naj u₁ in u₂ Ustrezne hitrosti delcev sprva. In biti v₁ in v₂ ustrezne končne hitrosti. Matematično se lahko koeficient restitucije izrazi na naslednji način:

Koeficient restitucije je dodaten znesek, saj je to razmerje med hitrostmi. Toda posredovane informacije so zelo zanimive:

- Če je ε = 0 enakovredno temu, da je V₂ = v₁. To pomeni, da so končne hitrosti enake in da je spopad neelastičen, kot je opisano v prejšnjem razdelku.

- Ko ε = 1 pomeni, da se relativne hitrosti pred in po nesreči ne spremenijo, je v tem primeru spopad elastičen.

- In če 0 < ε < 1 parte de la energía cinética de la colisión se transforma en alguna otra de las energías mencionadas anteriormente.

Kako določiti koeficient vračila?

Koeficient restitucije je odvisen od razreda gradiva, ki je vključen v trčenje. Zelo zanimiv test za določitev, kako je elastičen material za izdelavo kroglic, je, da spustite kroglico na fiksno površino in izmerite višino odbojke.

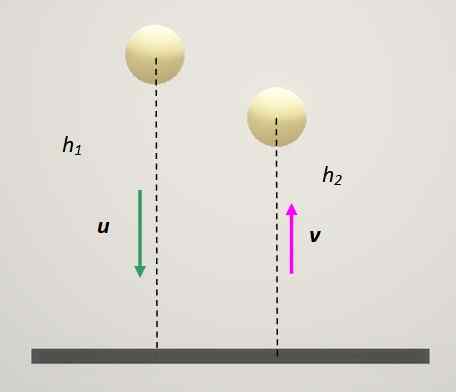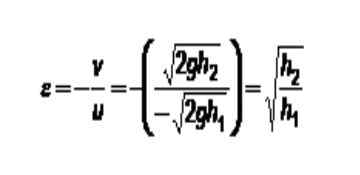
Slika 3. Metoda za določitev koeficienta restitucije. Vir: Self Made.

V tem primeru ima fiksna plošča vedno hitrost 0. Če je ta indeks 1 dodeljen temu in žoga je: indeks 2 ostaja:

Začetna hitrost je odvisna od višine h₁ iz katerega je padel:

Negativni znak označuje smer navzdol. In končna hitrost je povezana z največjo višino h₂ ki sega v skok:

Zamenjava v koeficientu restitucije imate:

Eksplozije

Na začetku je bilo predlagano, da se vso kinetično energijo spremeni s premikanjem na druge vrste energije. Navsezadnje energija ni uničena. Ali je mogoče, da se predmeti, ki so prišli z gibanjem? To si ni tako enostavno predstavljati.

Lahko vam služi: dinamika: zgodovina, kakšne študije, zakoni in teorije

Vendar si predstavljajmo, kaj se zgodi nazaj, kot v filmu, ki ga vidimo v hrbtu. Nato je bil predmet sprva počitek in nato eksplodira razdrobljenje na več delov. Ta situacija je popolnoma mogoča: to je eksplozija.

Tako da lahko eksplozijo obravnavamo kot popolnoma neelastično trčenje, ki ga v času vidimo nazaj. Ohranjena je tudi količina gibanja, ki lahko potrdi, da:

Str_tudi = P_F

Rešeni primeri

-Vaja 1

Iz meritev je znano, da je koeficient jeklene restitucije 0.90. Jeklena kroglica se spusti od 7 m visoko na fiksni plošči. Izračunati:

a) Dokler ne bo odskočila višine.

b) Kako dolgo traja prvi stik s površino in drugim.

Rešitev

a) Uporabljena je enačba, ki je bila prej sklenjena v razdelku o določitvi koeficienta restitucije:

Višina se očisti h₂:

0.90² . 7 m = 5.67 m

b) Dvignite 5.67 metrov hitrost, ki jo daje:

Od kje:

In čas, ki je potreben za dosego te višine, je:

t _Max = v_tudi/ g = (10.54/9.8 s) = 1.08 s.

Čas, potreben za vrnitev, je enak, torej skupni čas za nalaganje 5.67 metrov in vrnitev na izhodišče je dvakrat večji čas:

t_let = 2.15 s.

-Vaja 2

Slika prikazuje blok lesa mase m, ki visi na preostalih nitih dolžine l kot nihalo. Temu pravimo balistično nihalo in služi za merjenje hitrosti V vnosa masa mase m. Večja je hitrost, s katero krogla vpliva na blok, pri višji višini h bo to zgrajena.

Slikovna krogla je vdelana v blok, zato je popolnoma neelastični šok.

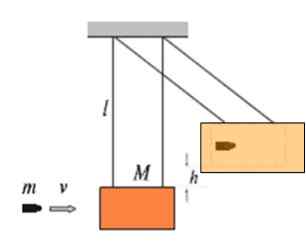Slika 4. Balistično nihalo.

Predpostavimo, da je 9 9.72 g Vpliv na masni blok 4.60 kg, nato se komplet dvigne na 16.8 cm ravnotežnega položaja. Kakšna je hitrost v krogla?

Rešitev

Med trkom je ohranjena količina gibanja in ali_F To je hitrost kompleta, ko je krogla vdelana v blok:

Str_tudi = P_F

Blok sprva počiva, medtem ko je krogla s hitrostjo usmerjena na cilj v:

m.v + m.0 = (m + m) u_F

 

Ni znano ali_F Tudi po trku se ohrani mehanska energija, kar je vsota gravitacijske potencialne energije in kinetične energije k:

Vam lahko služi: vsota vektorjev: grafična metoda, primeri, rešene vaje

Začetna mehanska energija = končna mehanska energija

In_mo = E_Mf

Ali_tudi + K_tudi = U_F + K_F

Gravitacijska potencialna energija je odvisna od višine, na kateri set doseže. Za ravnotežni položaj je začetna višina tista kot referenčna raven, torej:

Ali_tudi = 0

Zahvaljujoč krogle ima komplet kinetično energijo K_tudi, ki postane gravitacijska potencialna energija, ko set doseže največjo višino h. Kinetična energija daje:

K = ½ mV²

Sprva je kinetična energija:

K_tudi = (1/2) (m+m) u_F²

Ne pozabite, da krogla in blok tvorita en sam masni predmet M+ m. Gravitacijska potencialna energija, ko so dosegli na največji višini, je:

Ali_F = (M + M) GH

Zato:

K_tudi = U_F

(1/2) (m+m) u_F² = (M + M) GH

Zdaj je ta rezultat nadomeščen v izražanju v ki se je na začetku očistil, od ohranjanja količine gibanja:

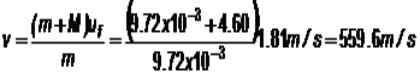
-Vaja 3

Predmet slike eksplodira v treh fragmentih: dva enaka masa m in ena večja od mase 2m. Slika prikazuje hitrosti vsakega fragmenta po eksploziji. Kakšen je bil prvi cilj predmeta?

Slika 5. Kamen, ki eksplodira v 3 fragmentih. Vir: Self Made.

Rešitev

Ta težava zahteva uporabo dveh koordinat: x in in, Ker imata dva fragmenta navpične hitrosti, preostala pa vodoravna hitrost.

Skupna masa predmeta je vsota mase vseh fragmentov:

M = m + m + 2m = 4m

Količina gibanja je ohranjena tako na osi x kot na osi y, predlaga se ločeno:

1. 4m. ali_x= m v₃
2. 4m. ali_in = m. 2V₁ - 2m. v₁

Upoštevajte, da se velik fragment premika navzdol s hitrostjo V1, da poudari to dejstvo, da je bil postavljen negativni znak.

Iz druge enačbe takoj sledi ali_in = 0, In prvi je takoj jasen UX:

Začetni cilj predmeta je bil u_tudi = u_x = v₃/4.

Reference

1. Giancoli, d.  2006. Fizika: načela z aplikacijami. 6^th. Ed Prentice Hall. 175-181
2. Rex, a. 2011. Osnove fizike. Pearson. 135-155.
3. Serway, r., Vulle, c. 2011. Osnove fizike. 9^na Cengage učenje. 172 -182
4. Tipler, str. (2006) Fizika za znanost in tehnologijo. 5. izd. Zvezek 1. Uredništvo se je vrtelo. 217-238
5. Tippens, str. 2011. Fizika: pojmi in aplikacije. 7. izdaja. MacGraw Hill. 185 -195