Središče gravitacijskih lastnosti, izračun, primeri

On Gravitacijski center telesa merljive velikosti je točka, kjer se šteje, da je njegova teža uporabljena. Je torej eden glavnih konceptov statične.

Prvi pristop pri osnovnih fizičnih težavah je domnevati, da se kateri koli predmet obnaša kot specifična masa, to pomeni, da nima dimenzij in celotna masa je koncentrirana v eni točki. To velja za škatlo, avto, planet ali subatomski delček. Ta model je znan kot Model delcev.

Slika 1. Na višini skok jih športnik popravi tako, da je njeno težišče zunaj telesa. Vir: Pixabay

Seveda je to pristop, ki daje zelo dobre rezultate za številne aplikacije. Ni lahka naloga upoštevati posamezno vedenje na tisoče in milijone delcev, ki bi jih lahko vsebovali kateri koli predmet.

Vendar je treba upoštevati resnične dimenzije stvari, če želite. Ker smo običajno v neposredni bližini Zemlje, je vedno prisotna sila na katerem koli telesu.

[TOC]

Pomisleki, da bi našli težišče 

Če bo upoštevana velikost telesa, kjer bo teža posebej uporabljena? Ko imate poljubno neprekinjen predmet, je njegova teža Porazdeljena sila med vsakim sestavnim delcem.

Naj te delce m₁, m₂, m₃… Vsak od njih doživi ustrezno gravitacijsko silo m₁g, m₂g, m₃G ..., vse vzporedno. To je tako, saj se gravitacijsko polje Zemlje v veliki večini primerov šteje za konstantno, glede na dejstvo, da so predmeti majhni v primerjavi z velikostjo planeta in so blizu njegove površine.

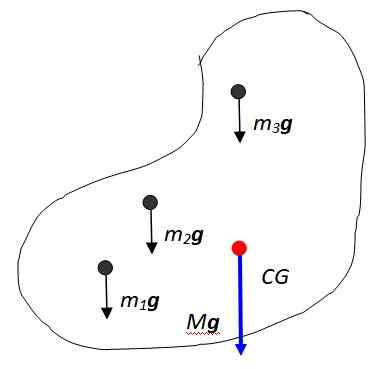Slika 2. Teža predmeta je porazdeljena masa. Vir: Self Made.

Vektorska vsota teh sil povzroči težo predmeta, ki se nanaša na točko, imenovano težišče, označeno na sliki kot CG, ki nato sovpada s Masovni center. Masovno središče je točka, ko je mogoče celotno maso šteti za koncentrirano.

Nastala teža ima velikost Mg kje M To je skupna masa predmeta in seveda je usmerjena navpično proti središču zemlje. Sumory zapis je koristen za izražanje celotnega telesa telesa:

Simetrični in homogeni predmeti, ki so enakovredni njihovi gostoti, so enotna, imajo svoje težišče v geometrijskem središču: kocke, paralelepipede, prstane, pnevmatike ali kroglice.

Gravitacijsko središče se ne ujema vedno z materialno točko. Na primer, CG obročev je v svojem geometrijskem središču, kjer ni samega testa. Kljub temu, če želite analizirati sile, ki delujejo na obroču, je treba težo uporabiti za to natančno točko.

V katerih primerih, v katerih je predmet poljubni, če je homogeni, lahko njegov masni center še vedno izračunamo z iskanjem Centroid o Baricentro slike.

Vam lahko služi: Merkur (planet)

Kako se izračuna središče gravitacije?

Načeloma, če je težišče (CG) in masno središče (CM) sovpadalo, ko je gravitacijsko polje enakomerno, potem lahko CM izračunamo in na njem uporabimo težo.

Razmislite o dveh primerih: prvi je tisti, v katerem je masna porazdelitev diskretna; to pomeni, da lahko preštejete vsako maso, ki tvori sistem, in dodelite številko I, kot je bilo storjeno v prejšnjem primeru.

Koordinate središča mase za diskretno masno porazdelitev so: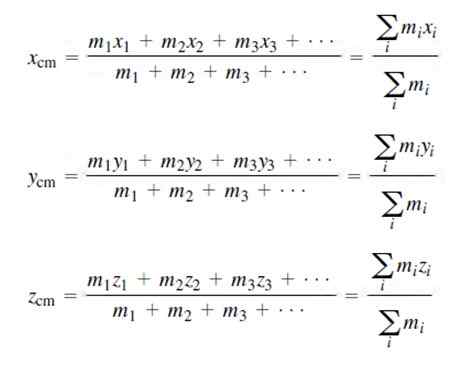

Seveda je vsota vseh mas enakovredna skupni masi M sistema, kot je navedeno zgoraj.

Tri enačbe so pri upoštevanju vektorja R zmanjšane na kompaktno obliko_cm o Položaj vektor masnega središča:

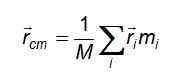
In v primeru neprekinjene porazdelitve mase, kjer so delci različne velikosti in jih ni mogoče razlikovati, da jih šteje, vsota nadomesti integral, ki je narejena o volumnu, ki ga zaseda zadevni objekt:

Kje r To je položaj vektorja diferencialne mase Dm In definicija masne gostote za izražanje mase je bila narejena Dm Vsebovano v volumskem diferencialu DV:

Gostota predmeta je lahko konstantna, v tem primeru izhaja iz integrala ali je funkcija prostorskih koordinat in moramo vedeti njegovo odvisnost od (x, y, z), da rešimo integral.

Lastnosti

Nekateri pomembni premisleki o množičnem centru so naslednje:

- Čeprav je za vzpostavitev položajev potreben referenčni sistem, središče mase ni odvisno od izbire, ki je narejena iz sistema, saj je lastnost predmeta.

- Ko ima predmet osi ali simetrijsko ravnino, je masno središče na omenjeni osi ali ravnini. Izkoristite to okoliščino prihrani čas izračuna.

- Vse zunanje sile, ki delujejo na objekt, se lahko uporabijo za masni center. Po sledenju te točke daje globalno predstavo o gibanju predmeta in olajša delo pri preučevanju njenega vedenja.

-Iskanje težišča telesa v statični bilanci

Recimo, da je telo prejšnje številke v statičnem ravnovesju.

Slika 3. Shema za izračun navora teže glede na točko oz.

Trenutek neto torzije glede na O, v skladu s sliko 3 je: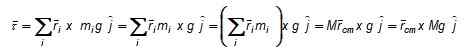A sila F, ki se je v težišču (ali tudi zgoraj ali spodaj, na osi, ki prehaja skozi njo, uporabila navpično navzgor. Obseg F je izbrana tako, da se objekt ne prenese in na ta način ga bomo imeli v statičnem ravnovesju.

Vam lahko služi: valovita optika

-Rešen primer

Tanka palica enotnega materiala ima dolžino 6 m in tehta 30 n. Na koncu se obesi 50 n zahoda in še 20 n na desnem koncu. Poiščite: a) Obseg naraščajoče sile, potrebne za vzdrževanje ravnotežja palice, b) Središče težišča.

Rešitev

Diagram sil je prikazan na naslednji sliki. Teža palice se nanese v njenem težišču, ki sovpada z njegovim geometrijskim središča. Edina dimenzija, ki je bila upoštevana, je njegova dolžina, saj izjava sporoča, da je tanka.

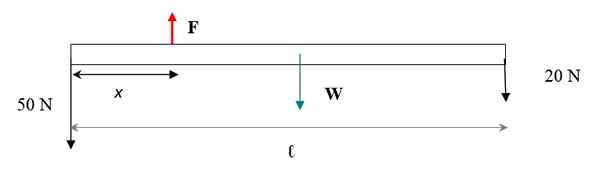Slika 4. Diagram pàra la barra.

Da sistem palice + ostane v prevajalskem ravnovesju, mora biti vsota sil nična. Sile so navpične, če razmislimo o znaku + in navzdol z znakom - potem:

F- 50- 20-30 n = 0

F = 100 n

Ta sila zagotavlja ravnovesje prevoda. Vzeti trenutke torzije vseh sil v zvezi z osi, ki poteka skozi levi konec sistema, in uporabimo definicijo:

t = r x f

Trenutki vseh teh sil glede na izbrano točko so pravokotni na ravnino palice:

t_F = xf = 100x

t_W = -(l/2) mg = -3m . 30 n = -90 n.m

t₁ = 0 (Ker sila 50 N prehaja skozi izbrano osi zavoja in ne izvaja trenutka)

t₂ = -Lf₂ = 6 m . 20 n = -120 n.m

Zato:

100 x -90 -120 n.M = 0

x = 2.10 m

Težišče palice + uteži se nahaja na 2.10 metrov od levega konca palice.

Razlika s sredino mase

Gravitacijsko središče sovpada s središčem mase, kot je navedeno, dokler je zemljiško gravitacijsko polje konstantno za vse točke predmeta, ki ga je treba upoštevati. Gravitacijsko polje Zemlje ni nič drugega kot dobro znana in znana vrednost G = 9.8 m/s² usmerjeno navpično navzdol.

Čeprav vrednost G doživlja razlike z širino in nadmorsko višino, običajno ne vplivajo na predmete, za katere se večino časa zdravi. Zelo drugače bi bilo, če bi veljalo za veliko telo v bližini Zemlje, na primer asteroid, ki bi bil blizu planeta.

Asteroid ima svoje masovno središče, vendar njeno težišče ne bi bilo treba več sovpadati s tem g Verjetno bi doživelo velike razlike v velikosti, glede na velikost asteroida in da uteži vsakega delca morda niso vzporedne.

Druga temeljna razlika je v tem, da je središče mase ne glede na to, ali obstaja sila, imenovana uporabljena teža na predmetu. To je notranja lastnost predmeta, ki razkriva, kako je njegova masa razporejena glede na njegovo geometrijo.

Vam lahko služi: kakšna je dielektrična konstanta?

Masovni center obstaja oboje, če se uporablja teža, kot da ne. In se nahaja v istem položaju, čeprav se predmet prenese na drug planet, v katerem je gravitacijsko polje drugačno.

Po drugi strani je težišče jasno povezano z uporabo teže, kot smo ga lahko cenili v prejšnjih odstavkih.

Primeri centra gravitacije

Težišče nepravilnih predmetov

Zelo enostavno je ugotoviti, kje je težišče nepravilnega predmeta kot skodelica. Najprej je suspendirana z katere koli točke in od tam je narisana navpična črta (na sliki 5 je linija fuchsije na levi sliki).

Potem je suspendirana z druge točke in narisana je nova navpična (turkizna črta na desni sliki). Presečišče obeh linij je središče teže skodelice.

Slika 5 . CG lokacija skodelice. Vir: Modified Pixabay.

Ravnovesje predmetov

Analiziramo stabilnost tovornjaka, ki kroži po cesti. Ko je težišče nad dno tovornjaka, se ne bo vlilo. Slika na levi je najbolj stabilen položaj.

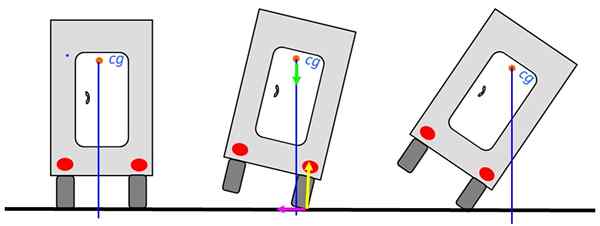Slika 6. Ravnotežje s tovornjakom. Vir: Self Made.

Tudi ko se tovornjak nagne v desno. Ko pa se bo ta linija prehodila zunaj tovornjaka.

Diagram prikazuje sile na točki podpore: normalno v rumeni, teža v zeleni in statični trenju na levi strani Fuchsia. Normalno in drgnjenje. Zato ne bodo prispevali k odlaganju tovornjaka.

Teža ostane, ki izvaja trenutek torzije, na srečo v proti -ogrodnem smislu in se ponavadi vrne v tovornjak v ravnotežni položaj. Upoštevajte, da navpična črta preide skozi podporno površino, ki je pnevmatika.

Ko je tovornjak v položaju skrajne desnice, se čas torzije teže spremeni in postane v napeti smeri. Če se ne moremo zoperstaviti drugemu, se bo tovornjak nalil.

Reference

1. Bauer, w. 2011. Fizika za inženiring in znanosti. Zvezek 1. MC Graw Hill.  247-253.
2. Giancoli, d.  2006. Fizika: načela z aplikacijami. 6. ... Ed Prentice Hall. 229-238.
3. Resnick, r. (1999). Fizično. Vol. 1. 3. izd. v španščini. Continental uredništvo s.Do. od c.V. 331-341.
4. Rex, a. 2011. Osnove fizike. Pearson.146-155.
5. Sears, Zemansky. 2016. Univerzitetna fizika s sodobno fiziko. 14. Ed. Zvezek 1.340-346.