Aksialna obremenitev Kako izračunane in rešene vaje

The Aksialna obremenitev To je sila, usmerjena vzporedno z osi simetrije elementa, ki tvori strukturo. Aksialna sila ali obremenitev je lahko napetost ali stiskanje. Če linija delovanja osne sile sovpada z osjo simetrije, ki poteka skozi sredino obravnavanega elementa.

Nasprotno, če gre za osno silo ali obremenitev, vzporedno z osi simetrije, vendar katerih linija delovanja ni na sami osi, je ekscentrična aksialna sila.

Slika 1. Aksialna obremenitev. Vir: Self Made

Na sliki 1 rumene puščice predstavljajo sile ali osne obremenitve. V enem primeru gre za koncentrično napetostno silo, v drugem pa se soočamo z ekscentrično kompresijsko silo.

Enota mera osne obremenitve v mednarodnem sistemu, če je Newton (N). Toda druge enote sile, kot sta kilogramska sila (kg-f) in trdnost funtov (LB-F), se pogosto uporabljajo (LB-F).

[TOC]

Kako se izračuna?

Za izračun vrednosti osne obremenitve v elementih strukture je treba upoštevati naslednje korake:

- Naredite diagram sile na vsakem elementu.

- Uporabite enačbe, ki zagotavljajo translacijsko ravnovesje, to je, da je vsota vseh sil nična.

- Razmislite o enačbi navorov ali trenutkov, tako da je rotacijsko ravnovesje izpolniti. V tem primeru mora biti vsota vseh navora nična.

- Izračunajte sile in določite aksialne sile ali obremenitve v vsakem od elementov.

Osnovna razmerja z aksialno obremenitvijo z običajnim naporom

Povprečni normalni napor je opredeljen kot količnik med osno obremenitev, razdeljen med prerezom območja. Enote normalnega truda v mednarodnem sistemu.Yo. So Newton na kvadratnem metru (N/ m²) ali Pascal (PA). Slika 2 prikazuje koncept normalnega truda za jasnost.

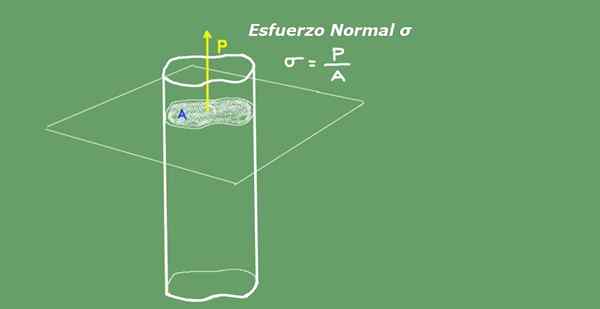Slika 2. Normalen napor. Vir: Self Made.

Rešene vaje

-Vaja 1

Razmislite o cilindričnem betonskem stolpcu H in radiu R. Predpostavimo, da je gostota betona ρ. Stolpec ne podpira nobene dodatne obremenitve kot lastna teža in je podprt na pravokotni bazi.

- Poiščite vrednost osne obremenitve v točkah A, B, C in D, ki so v naslednjih položajih: A na dnu stolpca, B A ⅓ višine H, C A ⅔ višine H in do zadnjega D na zgornjem koncu stolpca.

- Določite tudi povprečni normalni napor v vsakem od teh položajev. Vzemite naslednje številčne vrednosti: h = 3m, r = 20cm in ρ = 2250 kg/m³

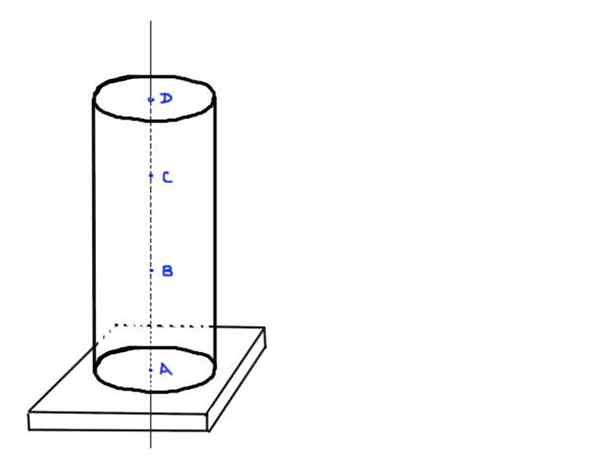Slika 3. Cilindrični stolpec. Vir: Self Made.

Rešitev

Skupna teža stolpca

Skupna teža W stolpca je produkt njegove gostote z volumnom, pomnoženim s pospeševanjem gravitacije:

W = ρ ∙ h ∙ π ∙ r² ∙ g = 8313 n

Aksialna obremenitev v a

V točki stolpca mora podpirati celotno težo, tako da je osna obremenitev na tej točki stiskanje enaka teži stolpca:

Pa = w = 8313 n

Aksialna obremenitev v B

V točki B bo sam ⅔ stolpca, tako da bo osna obremenitev na tej točki stiskanje in njegova ⅔ vrednost teže stolpca:

Pb = ⅔ w = 5542 n

Slika 3. Cilindrični stolpec. Vir: Self Made.

Zgornji položaj C Obstaja samo stolpec ⅓, zato bo njegova osna kompresijska obremenitev ⅓ lastna teža:

PC = ⅓ W = 2771 n

Aksialna obremenitev v D

Končno na točki D, ki je zgornji konec stolpca, ni obremenitve, zato je osna sila v tej točki praznina.

Pd = 0 n

Normalna prizadevanja na vsakem od položajev

Za določitev običajnega napora v vsakem od položajev bo treba izračunati presek območja A, ki je podan z:

A = π ∙ r² = 0,126m²

Na ta način bo običajni napor v vsakem položaju količnik med osno silo v vsaki od točk, razdeljenih med že izračunanim presekom, kar je v tej vaji enakov za vse točke, ker je stolpec cilindrično.

σ = p/a; σa = 66,15 kPa; σB = 44,10 kPa; σc = 22,05 kPa; σd = 0,00 kPa

-Vaja 2

Slika prikazuje strukturo, sestavljeno iz dveh palic, ki ji bomo rekli AB in CB. AB vrstica je podprta na koncu A za enega skozi zatič in na drugem koncu, povezana z drugim palico.

Podobno je CB vrstica podprta na koncu C s pomočjo zatiča in na koncu B s pin B, ki ga združuje v drugo palico. Na zatiče B ​​se uporabi navpična sila ali obremenitev F, kot je prikazano, kot prikazuje naslednja slika:

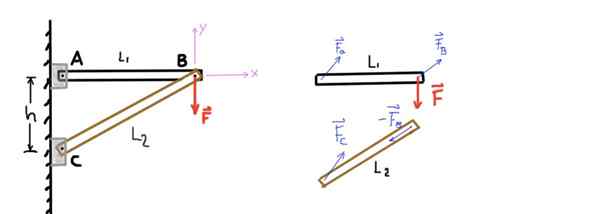Slika 4. Dve strukturi palic in diagram prostega telesa. Vir: Self Made.

Predpostavimo, da je teža palic zaničljiva, saj je sila F = 500 kg-F veliko večja od teže konstrukcije. Ločitev med podporo A in C je H = 1,5M, dolžina AB pa l1 = 2 m. Določite osno obremenitev v vsaki od vrstic, kar označuje, ali je osna stiskanje ali napetost.

Rešitev 2

Slika prikazuje s prostim telesnim diagramom sile, ki delujejo na vsak element strukture. Označen je tudi kartezijanski koordinatni sistem, s katerim bodo dvignjene ravnotežne enačbe sil.

Navodi ali trenutki bodo izračunani v točki B in bodo ocenjeni. Ravnotežje sil in navorov za vsako vrstico je:

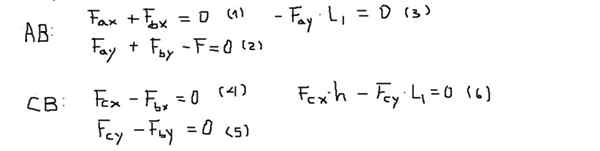
Potem so komponente sil vsake enačbe jasne po naslednjem vrstnem redu:

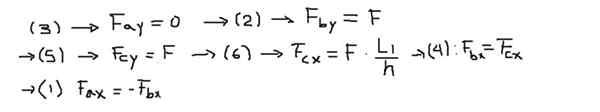
Končno se nastale sile izračunajo na koncih vsake palice:

Opozoriti je mogoče, da so sile na koncih vsake palice vzporedne z njimi, kar potrjuje, da gre za osne sile ali obremenitve. V primeru AB BAR je to osna napetostna sila, katere vrednost je:

F ∙ (L1/h) = 500 kg-f ∙ (2,0m/1,5m) = 666,6 kg-f = 6533,3 n

CB vrstica je v stiskanju zaradi obeh sil, ki delujeta na njihovih koncih, ki sta vzporedni s palico in kažejo na njihovo središče. Obseg osne stiskalne sile v CB palici je:

F ∙ (1 + l1²/h²) 1/2 = 500 kg-f ∙ (1 + (2/1,5) ²) 1/2 = 833,3 kg-f = 8166,6 n

Reference

1. Pivo f ... Mehanika materiala. 5. Izdaja. 2010. MC Graw Hill. 1-130.
2. Hibbeler R. Mehanika materialov. Osma izdaja. Dvorana Prentice. 2011. 3-60.
3. Gere J. Mehanika materialov. Osma izdaja. Cengage učenje. 4-220.
4. Giancoli, d. 2006. Fizika: načela z aplikacijami. 6. izd. Dvorana Prentice. 238-242.
5. Valera Negrete, J. 2005. Splošne zapise o fiziki. Ne. 87-98.