Definicija faktorične ploščadi, formule in vaje

On Faktorska ploščad To je preprost stroj, ki je sestavljen iz ureditve jermenice z multiplikacijskim učinkom sile. Na ta način lahko dvignete obremenitev z uporabo le enakovrednega dela teže na prostem koncu vrvi.

Sestavljen je iz dveh sklopov škripcev: ena, ki je pritrjena na podporo, in drugega, ki izvaja nastalo silo na obremenitvi. Srečnice so nameščene na splošno kovinskem okvirju, ki jih drži. 

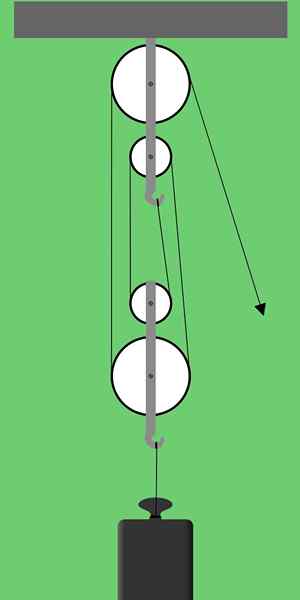
Slika 1. Shema faktoristične ploščice. Vir: Pixabay

Slika 1 prikazuje faktorsko ploščad, ki je sestavljena iz dveh skupin dveh jermenic. Imenovana tudi ta vrsta ureditve jermenice Serijska ploščad tudi Polipasti.

[TOC]

Faktorske desne formule

Primer 1: mobilna jermenica in fiksni

Da bi razumeli, zakaj ta ureditev pomnoži silo, bomo začeli z najpreprostejšim primerom, sestavljen iz fiksnega in mobilnega jermenice.

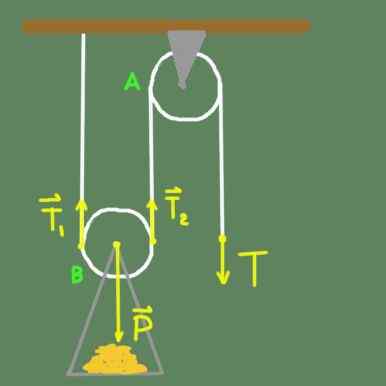Slika 2. Dve jermenici.

Na sliki 2 imamo s podporo fiksno jermenico do strehe. Jermenica A se lahko prosto vrti okoli svoje osi. Imamo tudi b jermenico, ki ima fiksno podporo na osi škripca, v kateri je obremenitev nameščena. Jermenica B, poleg tega, da se lahko prosto vrti okoli svoje osi, se lahko navpično premika.

Recimo, da smo v ravnovesju. Razmislite o silah, ki delujejo na B jermenico. Os b -pulley podpira skupno težo P, ki je usmerjena navzdol. Če bi bila to edina sila na jermenici B, vendar vemo, da vrv, ki poteka skozi to jermenico.

Za translacijsko ravnovesje morata biti obe sili enaki za težo, ki podpira osi škripca B.

T1 + t2 = p

Ker pa je jermenica B tudi v rotacijskem ravnovesju, potem T1 = T2. Sile T1 in T2 prihajajo iz napetosti, ki se nanaša na vrv, imenovano t.

Lahko vam služi: bohr atomski model

Zato t1 = t2 = t. Zamenjava v prejšnji enačbi ostaja:

T + T = P

2T = str

Nakazuje, da je napetost, ki se uporablja za vrv, le polovica teže:

T = P/2

Na primer, če bi bila obremenitev 100 kg, bi bilo dovolj, da na prostem koncu vrvi nanesete 50 kg sile, da bi tovora dvignila s konstantno hitrostjo.

Primer 2: Dva mobilna in dve fiksni škripci

Razmislimo o napetosti in sili, ki delujejo na nizu, ki je sestavljena iz dveh nosilcev podpornikov A in B z dvema škripcima.

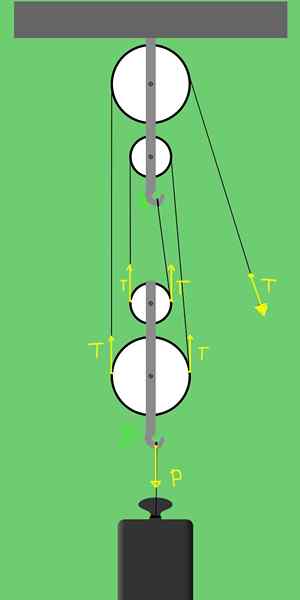Slika 3. Sile na ploščadi 2 fiksnih jermenic in 2 mobilnih škripcih.

Podpora B se lahko premakne navpično in sile, ki delujejo na sina:

- Teža P obremenitve, ki kaže navpično navzdol.

- Dve napetosti na veliki škripci in dve napetosti na majhnem škripcu. Skupno štiri napetosti, vse kažejo.

Da bi bilo translacijsko ravnovesje, je potrebno, da sile, ki navpično kažejo navzgor, enake obremenitvi, ki kaže. To pomeni, da ga je treba izpolniti:

T + T + T + T = P

To je 4 t = p

Od kod izhaja, da je uporabljena sila T na prostem koncu vrvi le četrtina teže zaradi obremenitve, ki se želi dvigniti., T = p / 4.

S to vrednostjo za T napetost lahko obremenitev vzdržujete statično ali naraščajo s konstantno hitrostjo. Če je bila uporabljena večja napetost od te vrednosti.

Splošni primer: N Mobilni škripci in N fiksni škripci

Kot je razvidno v prejšnjih primerih, je za vsako jermenico mobilnega nastanka nekaj sil navzgor po vrvi, ki gre skozi škripec. Toda ta sila ne more biti nič drugega kot napetost, ki se uporablja za vrv na prostem koncu.

Torej bo za vsak jermenici mobilnega nastavka prišlo do sile navzgor, ki je vredna 2T. Ker pa je v mobilnem kompletu N jermenice, je treba nato poudariti navpično navzgor: je:

Vam lahko postreže: motor s kletkami veverice

2 n t

Za navpično ravnovesje je potrebno:

2 N T = P

Zato je sila, ki se uporablja na prostem koncu,::

T = p / (2 n)

V tem primeru lahko rečemo, da sila, ki je na tovoran.

Na primer, če bi imeli faktorsko ploščad s 3 fiksnimi jermeni in 3 mobilnimi telefoni, bi bilo število n enako 3. Po drugi strani, če bi bila obremenitev p = 120 kg, bi bila sila, uporabljena na prostem koncu, t = 120 kg / (2*3) = 20 kg.

Rešene vaje

Vaja 1

Razmislite o faktorski ploščadi, sestavljeni iz dveh fiksnih škripcev in dveh mobilnih škripcev. Največja napetost, ki lahko podpira vrv, je 60 kg. Določite, kakšna je največja obremenitev, ki jo je mogoče postaviti.

Rešitev

Ko je obremenitev v mirovanju ali nenehno premikajo težo p le -te, je povezana s napetostjo T, ki se uporablja v vrvi z naslednjim razmerjem:

P = 2 n t

Ker gre za ploščad dveh mobilnih in dveh fiksnih škripcev, potem n = 2.

Največja obremenitev, ki jo je mogoče postaviti, dobimo, ko ima T največjo možno vrednost, kar je v tem primeru 60 kg.

Največja obremenitev = 2*2*60 kg = 240 kg

Vaja 2

Poiščite razmerje med napetostjo vrvi in ​​težo obremenitve, v faktorski ploščici dveh jermenic, v katerih se obremenitev pospeši s pospeševanjem.

Rešitev

Razlika v tem primeru glede na doslej opažena je, da je treba upoštevati dinamiko sistema. Zato predlagamo, da bi Newtonov drugi zakon našel zahtevano razmerje.

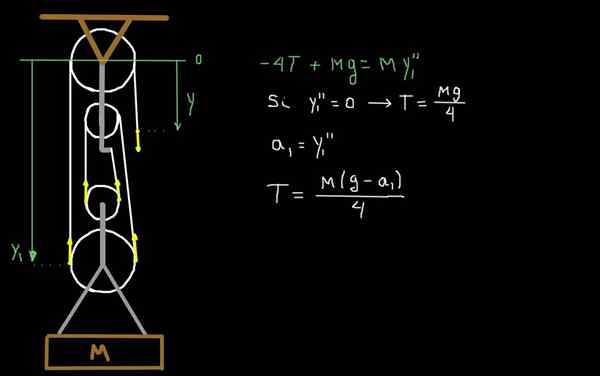Slika 4. Dinamika faktoristične ploščadi.

Na sliki 4 narišemo sile zaradi napetosti t vrvi. Mobilni del ploščadi ima skupno maso m. Kot referenčni sistem jemljemo na ravni prvega fiksnega in pozitivnega jermenice navzdol.

Y1 je najnižji položaj osi škripca.

Za določitev A1 pospeševanja mobilnega dela ploščadi uporabimo drugi zakon Newtona:

Vam lahko služi: teorem Varignon

-4 t + mg = m a1

Ker je teža obremenitve p = mg, kjer je G pospešek gravitacije, je mogoče zapisati prejšnje razmerje:

-4T + P = P (A1 / G)

Če bi želeli določiti napetost, uporabljena v vrvi, ko se določena obremenitev teže pospeši s pospeševanjem A1, bi bilo prejšnje razmerje takšno:

T = p (1 - a1 / g) / 4

Upoštevajte, da če bi bil sistem v mirovanju ali stalno premikal, potem A1 = 0, in smo si povrnili isti izraz, ki smo ga dobili v primeru 2.

Vaja 3

V tem primeru se uporablja enaka ploščad vaje 1 z isto vrvjo, ki podpira največ 60 kg napetosti. Določena obremenitev se dvigne in jo pospešuje od počitka na 1 m/s za 0,5 s z največjo napetostjo vrvi. Poiščite največjo težo obremenitve.

Rešitev

Izraze, pridobljene v vaji 2, in referenčnemu sistemu bomo uporabili na sliki 4, v katerem je pozitiven naslov navpičen navzdol.

Pospešek obremenitve je A1 = (-1 m/s -0 m/s) /0,5 s = -2 m/s^2.

Teža obremenitve v kilogramu je podana

P = 4 T / (1 - A1 / G)

P = 4*60 kg / (1 + 2/9.8) = 199,3 kg

To je največja možna teža obremenitve, ne da bi se vrv pokvarila. Upoštevajte, da je dobljena vrednost manjša od vrednosti, dobljene v primeru 1, v katerem je bila obremenitev predvidena z ničelnim pospeševanjem, torej v mirovanju ali konstantni hitrosti.

Reference

1. Sears, Zemansky. 2016. Univerzitetna fizika s sodobno fiziko. 14. Ed. Zvezek 1. 101-120.
2. Resnick, r. (1999). Fizično. Vol. 1. 3 rad. v španščini. Continental uredništvo s.Do. od c.V. 87-103.
3. Giancoli, d. 2006. Fizika: načela z aplikacijami. 6. Ed. Dvorana Prentice. 72 - 96.
4. Hewitt, Paul. 2012. Konceptualna fizikalna znanost. 5. Ed. Pearson.38-61.
5. Serway, r., Jewett, J. (2008). Fizika za znanost in inženiring. Zvezek 1. 7. Ed. Cengage učenje. 100 - 119.